강화학습 기초

1. 강화학습의 기본 구조

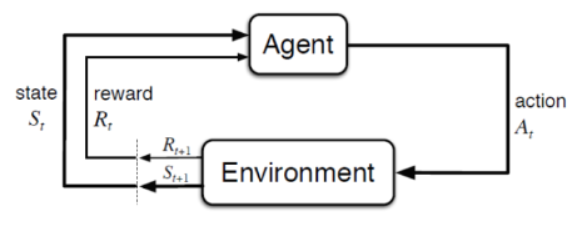
• Agent(에이전트)가 Environment(환경)와 상호작용하며 강화학습의 목표는 Environment(환경)에서 Agent가 최대 reward를 얻을 수 있도록 Agent(에이전트)를 학습하는 것이다.

• Agent(에이전트) : 주어진 문제 상황에서 행동하는 주체이다.

• Environment(환경) : 문제 세팅 그 자체를 의미하며 Agent가 취할 수 있는 행동, 그에 따른 보상 등 게임 자체의 모든 규칙이 Environment(환경)이 된다.

  • 강화학습에서는 Environment(환경)을 Markov property(마르코프 특성)으로 가정한다.

• Agent가 Environment(환경)에서 Action(행동)을 하기 위한 의사 결정 과정을 수학적으로 풀기 위해서 마르코프 결정 과정(Markov Decision Process)으로 모델링한다.

2. 마르코프 결정 과정(Markov Decision Process)

• 마르코프 결정 과정(Markov Decision Process)은 (S, A, P, R, γ) 로 표현되며 마르코프 프로세스(Markov Process)의 확장된 형태이다.

  • S(state) : 현재 시점에서 상태(상황)이 어떤지 나타내는 값들의 집합.

  • A(action) : Agent가 취할 수 있는 선택지(행동)를 나타내는 값들의 집합이다.

  • P(probability) : 상태(S)에서 다른 상태(S')로 전이될 확률(상태 이행 확률)을 의미한다.

    

  • R(reward) : Agent가 환경으로부터 현재 상태에서 다음 상태로 진행될 때마다 받는 상태의 가치를 스칼라 값으로 정량화하였다.

    

  • γ(discount factor) : 가까운 미래와 먼 미래에 얻을 수 있는 R(reward)의 정도를 조절하는 변수이다.

• π(policy) : policy(정책)은 Agent(에이전트)가 이전 상태(S)에서 다음 상태(S')로 행동(A)을 이동시키는 방식이다.

• 최적 정책의 목표는 누적 보상을 많이 받을 수 있는 정책을 찾는 것이다.

• 마르코프 프로세스(Markov Process)는 마르코프 특성(Markov property)을 지니는 이산 시간(discrete time) 확률 과정(stochastic process)이다.

• 이산 시간 확률 과정(discrete time stochastic process): 시간(time interval)이 이산적(discrete)이고 현재의 상태(state)가 이전 상태(state)에만 영향을 받는 확률 과정이다. (이때 확률은 상태 이행 확률이다.)

• 마르코프 특성(Markov property)이란 과거 상태들(S1, S2,..., St−1)과 현재 상태(St)가 주어졌을때, 미래 상태(St+1)는 과거 상태와는 독립적으로 현재 상태에 의해서만 결정되는 것을 말한다.

• 마르코프 프로세스(Markov Process)는 상태(S)와 상태 이행 확률(P)로 구성되며, P는 상태 S에서 S’으로 전이될 확률을 나타낸다.

• 마르코프 프로세스(Markov Process)는 시간 t에서의 상태는 t−1에서의 상태에만 영향을 받는다라고 말할 수 있다.

3. 마르코프 보상 프로세스(Markov Reward Process)

• 마르코프 프로세스(Markov Process)에서는 각 상태별 전이될 확률(P)이 주어져 있지만 이전 상태(S)에서 다음 상태(S')로 가치 평가가 없다.

• 보상(reward)과 감가율(discount factor)을 추가하며 보상(reward)는 가치를 정량화하고 감가율(discount factor)는 보상(reward)의 정도를 조절한다.

• Agent(에이전트)는 가치함수(value function)을 활용하여 보상(reward)이 최대인 상태(S)를 찾는다.

3.1 상태 가치 함수(state value function)

• 현재 상태(S)에서 다음 상태(S')들의 집합으로 보상(reward)에 대한 기댓값이 정해지는 데 각 상태(S')를 평가하는 것이 상태 가치 함수(state value fuction)이다.

• Gt(누적 보상 함수)는 시간 t 이후로부터 얻을 수 있는 보상의 합을 의미하고 감가율(γ)을 통해 다음과 같이 정의한다.

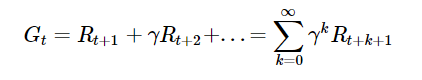
• 감가율(γ)이 0에 가까워지면 근시안적인 평가를 하게되어 가까운 미래만 고려하게 된다.

• 감가율(γ)이 1에 가까워지면 먼 미래까지 평가하게 되어 거의 모든 보상값을 고려하게 된다.

• 감가율(γ)은 미래의 보상은 현재의 보상보다 가치가 낮음을 의미하고 감가율을 조정하여 가치의 정도를 조정할 수 있다.

• 정책 π에 의해서 행동들이 결정되고 결정된 행동들에 의해서 상태들도 정해진다. 상태 가치 함수는 현재 상태 s에서 정책 π를 따랐을 때의 가치를 반환한다.

3.2 상태 행동 가치 함수(action state value function)

• 상태 가치 함수(state value function)을 통해서 더 높은 가치를 갖는 다음 상태(S')를 선택하여 현재 상태(S)를 이동시킨다.

• 상태 행동 가치 함수는 이전 상태(S)에서 행동(A)를 수행했을 때 다음 상태(S')에 대한 가치를 반환한다.

• 상태 행동 가치 함수는 Q - value를 구하기 위해 사용된다.

• 정책 π에 의해서 행동들이 결정되고 결정된 행동들에 의해서 상태들도 정해진다. 현재 상태 s에서 정책 π를 따라 행동 a를 수행했을 때의 가치의 기댓값이 반환(Q-value)된다.

3.3 벨만 방정식(Bellman equation)

• 가치함수로부터 기댓값을 계산하려면 앞으로 받을 모든 보상에 대해 고려해야지만 물리적으로 계산하기 무리가 있다.

• 벨만 방정식을 사용하면 여러 번의 연속적인 계산으로 가치함수의 참 값을 알아낸다.(가치함수 업데이트)

• 벨만 방정식은 상태 가치 함수와 상태 행동 가치 함수의 관계를 나타내는 방정식이다.

• 벨만 기대 방정식(Bellman expectation equation) : 현재 상태의 가치함수와 다음 상태의 가치함수 사이의 관계를 식으로 나타낸 것이다.

  • 상태 가치 함수
    

  • 상태 행동 가치 함수

• 벨만 최적 방정식(Bellman optimality equation) : 최적 가치 함수를 현재 상태의 최적 가치 함수와 다음 상태의 최적 가치 함수 사이의 관계로 나타낸 것이다.

  • 최적 가치 함수 : 현재 상태에서 앞으로 가장 많은 보상을 받을 정책을 따랐을 때의 가치함수이다. 즉, 현재 환경에서 취할 수 있는 가장 높은 값의 보상 총합이다.

  • 최적 상태 가치
    

  • 최적 상태 행동 가치