(논문 요약) Approximate Entropy and Sample Entropy: A Comprehensive Tutorial by Alfonso Delgado-Bonal and Alexander Marshak (1)

DongYoung Kim·2022년 8월 16일
approximate entropyentropysample entropy엔트로피
0

재미있는 논문 요약

목록 보기
2/2
post-thumbnail

본 글은 위키백과
https://en.wikipedia.org/wiki/Conditional_entropy
에서 motivation 그리고 property 부분과 논문
Shannon, C. E. (1948). A mathematical theory of communication. The Bell system technical journal, 27(3), 379-423.ISO 690
및
Delgado-Bonal, A., & Marshak, A. (2019). Approximate entropy and sample entropy: A comprehensive tutorial. Entropy, 21(6), 541.
를 참고하였음을 밝혀드립니다.

문제 제기

이 논문에서는 어떠한 데이터의 series가 주어졌을 때, 이 데이터가 얼마나 random한지에 대한 측량 방식을 소개합니다. 사실 Shannon(1948)에 의해 처음으로 정보의 측량 단위가 엔트로피 위주로 정해졌지만, 이는 frequentist의 관점으로서 무한히 많은 데이터가 주어졌을 때 각 symbol이 나올 수 있는 확률 공간을 위주로 정의한 것이라는 제약이 있습니다. 예를 들어 다음과 같은 두 가지 series가 있다고 합시다.

A:01010101010101010101A: 01010101010101010101
B:01101000110111100010B:01101000110111100010

두 series AA와 BB는 모두 1을 10개, 0을 10개 씩 포함하고 있습니다. 만약 series에서 1이 나타날 확률과 0이 나타날 확률이 모두 0.5라고 가정할 경우, Shannon의 엔트로피 정의에 의하면 두 series는 같은 정보량을 가지고 있게 됩니다. 하지만 사실 우리는 주어진 패턴을 통해 series AA 다음에 나올 숫자는 0일 확률이 높고, series BB 다음에 나올 숫자는 알 수 없다는 사실을 예측할 수 있습니다. 즉 entropy는 series의 다음에 실제로 나오는 값에 관심이 있는 것이 아닌, 각 데이터의 symbol이 나오는 빈도 위주로 정보를 측정한 것일 뿐이라는 사실을 확인할 수 있습니다.

Entropy에 대한 정의

데이터가 어떤 확률 공간 (S,P,P[⋅])(\mathcal{S}, \mathcal{P}, P[\cdot])을 따르는 event XX로 정의된다고 합시다. 그렇다면 그 데이터의 entropy는 다음과 같이 정의할 수 있습니다.

H(X)=−∑x∈SP[x]⋅log⁡(P[x]))H(X)=-\sum_{x \in \mathcal{S}}P[x] \cdot \log (P[x]))

이번엔 이 데이터가 두 개의 시계열 데이터로 이루어졌다고 가정하고, 첫 번째를 random variable X∼(X,PX,PX[⋅])X \sim (\mathcal{X}, \mathcal{P}_X, P_X[\cdot]), 두 번째를 Y∼(Y,PY,PY[⋅])Y \sim (\mathcal{Y}, \mathcal{P}_Y, P_Y[\cdot])라고 합시다. 이 joint event에 대한 확률공간을 (W,PX,Y,PX,Y[⋅,⋅]), where W=X×Y(\mathcal{W}, \mathcal{P}_{X,Y}, P_{X,Y}[\cdot, \cdot]), \, where \, \mathcal{W}=\mathcal{X} \times \mathcal{Y} 로 둘 때, joint entropy는 다음과 같이 구할 수 있습니다.

H(X,Y)=−∑x∈X,y∈YPX,Y[x,y]⋅log⁡PX,Y[x,y]H(X, Y) = -\sum_{x \in X, y \in Y}P_{X,Y}[x, y] \cdot \log P_{X,Y}[x, y]

두 확률 변수가 주어졌을 때, 이에 대한 conditional probability를 정의할 수 있듯, 마찬가지로 conditional entropy를 정의할 수 있습니다. 주의할 점은, conditional probability는 두 확률 변수 중 한 확률 변수의 상태가 정해졌을 때, 이에 따라 결정되는 다른 확률 변수의 확률을 정의한 것이라면, conditional entropy는 한 확률 변수 전체의 상태를 고려한 다른 확률 변수의 엔트로피라는 사실입니다.
예를 들어, 확률 변수 XX의 상태가 x∈Xx \in X로 주어졌을 때, 확률공간 YY의 conditional probability에 대한 엔트로피는 다음과 같이 계산됩니다.

H(Y∣X=x)=−∑y∈YPX,Y[Y=y∣X=x]⋅log⁡PX,Y[Y=y∣X=x]H(Y|X=x)=-\sum_{y \in \mathcal{Y}}P_{X, Y}[Y=y|X=x] \cdot \log P_{X, Y}[Y=y|X=x]

그렇다면 conditional entropy는, 위에서 구한 conditional probability에 대한 엔트로피에다가, 각 x∈Xx \in \mathcal{X}에 대해 PX[X=x]P_{X}[X=x]를 곱해서 더한 값, 즉 weighted sum을 계산한 값입니다. 이를 식으로 정리하면 다음과 같습니다.
Conditional entropy H(Y∣X)H(Y|X) is given as:

H(Y∣X)=∑x∈XPX[x]H(Y∣X=x)=−∑x∈XPX[x]∑y∈YPX,Y[Y=y∣X=x]⋅log⁡PX,Y[Y=y∣X=x]=−∑x∈X∑y∈YPX[x]⋅PX,Y[Y=y∣X=x]⋅log⁡PX,Y[Y=y∣X=x]=−∑x∈X,y∈YPX,Y[Y=y,X=x]⋅log⁡PX,Y[Y=y∣X=x]H(Y|X) = \sum_{x \in \mathcal{X}}P_{\mathcal{X}}[x]H(Y|X=x)\\ =-\sum_{x \in \mathcal{X}}P_{\mathcal{X}}[x]\sum_{y \in \mathcal{Y}}P_{X, Y}[Y=y|X=x] \cdot \log P_{X, Y}[Y=y|X=x]\\ =-\sum_{x \in \mathcal{X}}\sum_{y \in \mathcal{Y}}P_{\mathcal{X}}[x] \cdot P_{X, Y}[Y=y|X=x] \cdot \log P_{X, Y}[Y=y|X=x]\\ = -\sum_{x \in \mathcal{X}, y \in \mathcal{Y}}P_{X, Y}[Y=y, X=x] \cdot \log P_{X, Y}[Y=y|X=x]

위 결과들을 종합해본다면, 다음과 같은 관계식을 구할 수 있습니다.

H(X,Y)=−∑x∈X,y∈YPX,Y[x,y]⋅log⁡PX,Y[x,y]=−∑x∈X,y∈YPX,Y[Y=y,X=x]⋅log⁡(PX,Y[Y=y∣X=x]⋅PX[X=x])=H(Y∣X)−∑x∈X,y∈YPX,Y[Y=y,X=x]⋅log⁡PX[X=x]=H(Y∣X)−∑x∈Xlog⁡PX[X=x]⋅∑y∈YPX,Y[Y=y,X=x]=H(Y∣X)+H(X);H(X, Y) = -\sum_{x \in X, y \in Y}P_{X,Y}[x, y] \cdot \log P_{X,Y}[x, y] \\ =-\sum_{x \in \mathcal{X}, y \in \mathcal{Y}}P_{X, Y}[Y=y, X=x] \cdot \log (P_{X, Y}[Y=y|X=x] \cdot P_{X}[X=x]) \\ =H(Y|X)-\sum_{x \in \mathcal{X}, y \in \mathcal{Y}}P_{X, Y}[Y=y, X=x] \cdot \log P_{X}[X=x] \\ =H(Y|X)-\sum_{x \in \mathcal{X}} \log P_{X}[X=x] \cdot \sum_{y \in Y}P_{X, Y}[Y=y, X=x]\\ =H(Y|X)+H(X);

In the same way,

H(X,Y)=−∑x∈X,y∈YPX,Y[Y=y,X=x]⋅log⁡(PX,Y[X=x∣Y=y]⋅PY[Y=y])=H(X∣Y)+H(Y);H(X, Y) = -\sum_{x \in \mathcal{X}, y \in \mathcal{Y}}P_{X, Y}[Y=y, X=x] \cdot \log(P_{X, Y}[X=x|Y=y] \cdot P_{Y}[Y=y]) \\ =H(X|Y)+H(Y);

Stochastic process and deterministic process

우리가 데이터 series X=(X1,X2,X3,...,XT)X=(X_1, X_2, X_3, ..., X_T)를 관찰한다고 할 때, conditional entropy는 다음과 같을 것입니다.

H∗(X)=lim⁡T→∞H(XT∣XT−1,XT−2,...,X1);H^*(X)=\lim_{T \rightarrow \infin} H(X_T|X_{T-1}, X_{T-2}, ..., X_1);

그리고, 각 random variable에 해당하는 entropy의 평균을 구하면 다음과 같으며, 이를 entropy rate라고 정의합니다.

H(X)=lim⁡T→∞1TH(X1,X2,...,XT)H(X)=\lim_{T \rightarrow \infin} \frac{1}{T}H(X_1, X_2, ..., X_T)

만약 데이터들이 모두 independent and identically distributed (i.e., i.i.d) 조건을 만족한다면, 무한히 많은 데이터를 관측한다고 해도 조건에 의해 다음과 같은 관계식이 성립합니다.

H(X)=H∗(X)=H(Xi),  i∈N;H(X)=H^*(X)=H(X_i), \, \, i \in \mathbb{N};

따라서, 각 데이터 포인트의 순서가 어떠한지는 전혀 상관이 없고, 모든 데이터의 entropy에 대한 평균, 즉 entropy rate가 바로 시간 TT에서의 conditional entropy라는 사실을 알 수 있습니다.
어떤 information source가 memoryless하다면, 그 source가 생성해내는 message가 i.i.d한 조건을 만족할 것입니다. 이러한 process를 바로 "stochastic process"라고 합니다. 하지만 만약 과거의 데이터 값이 미래의 데이터 값을 영향을 주어서, conditional entropy값이 그저 entropy의 평균을 구한 것과는 완전히 다른 값을 취한다면 어떻게 될까요?
이러한 경우를 바로 deterministic process, 혹은 chaotic process라고 하며, 이는 dynamic system에 적용되는 경우가 많습니다. 처음에 정의했던 message AA와 BB를 다시 기억해봅시다.

A:01010101010101010101A: 01010101010101010101
B:01101000110111100010B:01101000110111100010

Message AA의 경우, 숫자 '01'이 반복되기 때문에, 이를 압축시킬 경우 "message AA는 숫자 '01'이 10번 반복된다"라고 줄일 수 있을 것입니다. 하지만 message BB의 경우 더 이상 압축시키는 것이 힘들 것입니다. 이러한 압축시킬 수 있는 최소한의 length를 'Komogorov complexity'라고 합니다. 만약 메시지가 너무 random해서 더 이상 압축이 불가능할 경우, complexity는 메시지의 length 그 자체일 것입니다.
이런 방식으로, complexity와 shannon entropy를 일반화하여, dynamic system에 대한 entropy를 계산하고자 한 것이 바로 Kolmogorov-Sinai(KS) entropy입니다. 하지만 KS entropy 또한 signal이 noisy한 상황에서 사용의 제약이 있다는 한계가 있습니다. 이를 해결하려고 Grassberger와 Procaccia는 다음과 같이 information rate를 정의하였습니다.

Cd(r)=lim⁡N→∞1N[number of pairs (n,m) with (∑i=1d∣Xn+i−Xm+i∣2)12≤r]C_d(r)=\lim_{N \rightarrow \infin} \frac{1}{N}[number \, of \, pairs \, (n, m) \, with \, (\sum^{d}_{i=1}|X_{n+i}-X_{m+i}|^2)^\frac{1}{2} \le r]

이를 분석하면 다음과 같습니다. 길이가 무한히 긴(N→∞N \rightarrow \infin) 신호에 대해, window size가 dd인 신호로 자릅니다. 또한 잘라진 신호끼리 distance를 측정하여, 그 distance가 rr 이하인 경우를 count하여, 이를 NN으로 나눈 것이 바로 Cd(r)C_d(r)입니다.

Cd(r)C_d(r)의 의미가 무엇일까요?

window size 가 d−1d-1일 때, 서로 다른 두 window Xn+iX_{n+i}, Xm+iX_{m+i}가, i=0,1,...,d−2i=0, 1, ... , d-2에 대해서

∣Xn+i−Xm+i∣2)12≤r|X_{n+i}-X_{m+i}|^2)^\frac{1}{2} \le r

를 만족한다고 합시다. 정의에 의해 이 때의 information rate가 바로 Cd−1(r)C_{d-1}(r)입니다.이와 같은 사실이 주어졌을 때, window 바깥 쪽 첫 번째 점, 즉 Xn+(d−1)X_{n+(d-1)}, Xm+(d−1)X_{m+(d-1)} 사이의 distance가 rr 이하일 conditional entropy는 어떻게 될까요? 아이디어는, conditional entropy를 구하는 식은 다음과 같다는 사실입니다.

H(Y∣X)=H(X,Y)−H(X)H(Y|X)=H(X, Y) - H(X)

이 때 H(X,Y)H(X, Y)는 log⁡(Cd−1(r))\log(C_{d-1}(r))에, H(X)H(X)는 Cd(r)C_{d}(r)에 대응할 수 있습니다. 즉, d−1d-1개의 data point가 주어질 때, 그 다음 data point에 해당하는 conditional entropy가 높을수록 해당 series는 예측 불가능하고, conditional entropy가 낮을수록 생성되는 정보량이 적기 때문에 예측 가능한 data series라는 사실을 추론할 수 있습니다.

Approximate entropy

따라서 approximate는 위에서 정의한 Cd(r)C_d(r)을 일반화한 measure이라고 할 수 있으며, 먼저 비슷하게 생긴 Cim(r)C_i^m(r)은 다음과 같습니다.

Given a sequence of numbers

u={u(1),u(2),...,u(N)}u = \{u(1), u(2), ... ,u(N)\}

of length NN, a non-negative integer mm, with m≤Nm \le N and a positive real number rr, we define the blocks

x(i)={u(i),u(i+1),...,u(i+m−1)}x(i) = \{u(i), u(i+1), ... , u(i+m-1)\}

and

x(j)={u(j),u(j+1),...,u(j+m−1)}x(j) = \{u(j), u(j+1), ... , u(j+m-1)\}

, and calculate the distance between them as

d[x(i),x(j)]=maxk=1,2,...,m(∣u(i+k−1)−u(j+k−1)∣).d[x(i), x(j)] = max_{k=1,2, ... , m}(|u(i+k-1)-u(j+k-1)|).

Then we calculate the value

Cim(r)=(number of j≤N−m+1) such that d[x(i),x(j)]≤rN−m+1;C_i^m(r) = \frac{(number \, of \, j \le N-m+1) \, such \, that \, d[x(i), x(j)] \le r}{N-m+1};

즉, 분자 부분은 resolution rr에 대해, 주어진 block x(i)x(i)와 비슷한 block들을 센 개수를 의미합니다.
그 다음, ϕm(r)\phi^m(r)이라는 함수를 정의합니다:

ϕm(r)=∑i=1N−m+1log⁡(Cim(r))N−m+1\phi^m(r) = \frac{\sum^{N-m+1}_{i=1}\log(C^m_i(r))}{N-m+1}

그 뒤에, 우리는 ApEnApEn을 다음과 같이 정의할 수 있습니다.

ApEn(m,r,N)(u)=−(ϕm+1(r)−ϕm(r)) ApEn(m, r, N)(u) = -(\phi^{m+1}(r) - \phi^m(r)) \,
with m≥1 and ApEn(0,r,N)(u)=−ϕ1(r)with \, m \ge 1 \, and \, ApEn(0, r, N)(u) = - \phi^1(r)

ApEnApEn의 의미

논문에서는 −ApEn(m,r,N)-ApEn(m, r, N)를 다음과 같이 설명합니다.

−ApEn(m,r,N)(u)=ϕm+1(r)−ϕm(r)=average  over  i  of  the  log⁡(conditional  probability  of  ∣u(j+m)−u(i+m)∣  ≤  r,  if  it  is  verified  that  ∣u(j+k)−u(i+k)∣≤r  for  k=0,1,...,m−1)-ApEn(m, r, N)(u) = \phi^{m+1}(r) - \phi^m(r) \\ = average \; over \; i \; of \; the \; \\ \log(conditional \; probability \; of \; |u(j+m)-u(i+m)| \; \le \; r, \; \\ if \; it \; is \; verified \; that \\ \; |u(j+k)-u(i+k)| \le r \; for \; k=0, 1, ..., m-1)

다시 말해, x(i)x(i)와 x(j)x(j)가 k=0k=0부터 m−1m-1까지 ∣u(j+k)−u(i+k)∣≤r|u(j+k)-u(i+k)| \le r를 만족한다는 사실이 주어졌을 때, 그 다음 data point인 ∣u(j+m)−u(i+m)∣≤r|u(j+m)-u(i+m)| \le r를 만족하는지에 대한 여부를 묻고 있는 것입니다.

이는 위에서 정의한 conditional entropy H(Y∣X)=H(X,Y)−H(X)H(Y|X)=H(X, Y) - H(X)를 떠오르면 이해가 갑니다. 이 때 H(Y∣X)H(Y|X)는 −ApEn(m,r,N)(u)-ApEn(m, r, N)(u)에, H(X,Y)H(X, Y)는 ϕm+1(r)\phi^{m+1}(r)에, 그리고 H(X)H(X)는 ϕm(r)\phi^m(r)에 대응시킬 수 있습니다. 거칠게 말하면, ϕm(r)\phi^m(r)는 m+1m+1 번째 데이터 포인트에서 match가 될 수 있는 후보들의 수를 센 것이고, ϕm+1(r)\phi^{m+1}(r)은 실제로 m+1m+1 번째 데이터 포인트에서 match가 생긴 경우를 센 것입니다.
따라서 ApEnApEn은 다음과 같은 성질들을 가지고 있습니다.

  • ApEn은 모델에 독립적으로 모든 데이터 종류에 대해 적용 가능합니다.
  • 평균, 분산과 같은 MGFMGF 함수를 사용하는 경우 outlier의 발생에 굉장히 민감하지만, ApEnApEn의 경우 Shannon의 entropy와 같이 outlier에 robust합니다.
  • ApEnApEn은 완벽하게 regular series에 대해 값 0을 가지며, 모든 data에 대해 항상 양수 값을 가집니다.
  • Shannon entropy와 비슷하게, 완벽히 random인 binary series에 대해서는 log2log2 값을 가지며, symbol k에 대해선 log⁡k\log k값을 가집니다.
  • ApEnApEn은 uniform한 scaling에 대해서는 변하지 않지만, coordinate transformation에 대해서는 변하기 때문에, scale은 반드시 고정되어야 합니다.
  • 비선형성은 ApEnApEn값을 더 늘립니다.
  • Raw data에 대해서도 적용 가능하지만, 데이터에 나타나는 모든 trend를 제거하는 과정이 필수적입니다.
  • m 값은 2, 3 정도의 낮은 값이 적당하며, r은 0.1에선 0.25에 std를 곱한 값이 적당합니다.
  • 데이터 포인트는 10m10^m에서 30m30^m개 정도가 적당합니다.
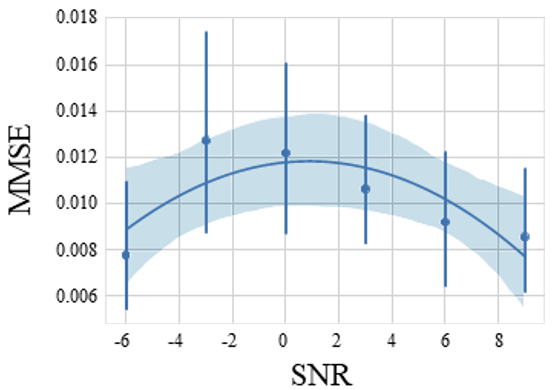
  • SNR이 3보다 낮을 경우, ApEn은 취약성을 보입니다.
  • 두 데이터를 비교하기 위해선, normalization이 필요합니다.
  • ApEn은 signal이 생성되는 과정에 대한 어떠한 확률 모델에 대한 가정도 필요하지 않습니다.
  • Sampling 간격이 균일해야 합니다.
  • Cim(r)C_i^m(r)은 x(i)x(i)와 x(i)x(i)를 비교하는 것까지 count하기 때문에, match의 개수가 낮을 경우 bias가 20~30%까지 발생할 수 있습니다.

글이 너무 길어진 것 같아, 다음 글에 이어서 ApEnApEn의 단점을 보완한 SampleEnSampleEn에 대해 설명해보겠습니다. 감사합니다!

profile
DongYoung Kim
Bayesian, System engineer, Evangelist
이전 포스트

(논문 요약) Approximate Entropy and Sample Entropy: A Comprehensive Tutorial by Alfonso Delgado-Bonal and Alexander Marshak (2)

0개의 댓글