• 이 블로그에선 np.sum을 활용하여 axis 에 대해 알아보겠음.

Data Type of Linear Algebra

Scalar

• 하나의 숫자만으로 이루어진 data
• $x∈R$

Vector

• 일반적인 일차원 배열
• 하나의 vector를 이루는 data의 개수를 dimension이라 함.

Matrix

• 복수의 dimension을 가지는 data가 다시 여러 개 있는 경우의 data를 합쳐서 표기한 것
• 일반적으로 2차원 배열이 행렬

Tensor

• 3차원 이상의 배열을 tensor라고 함

다차원 배열의 axis

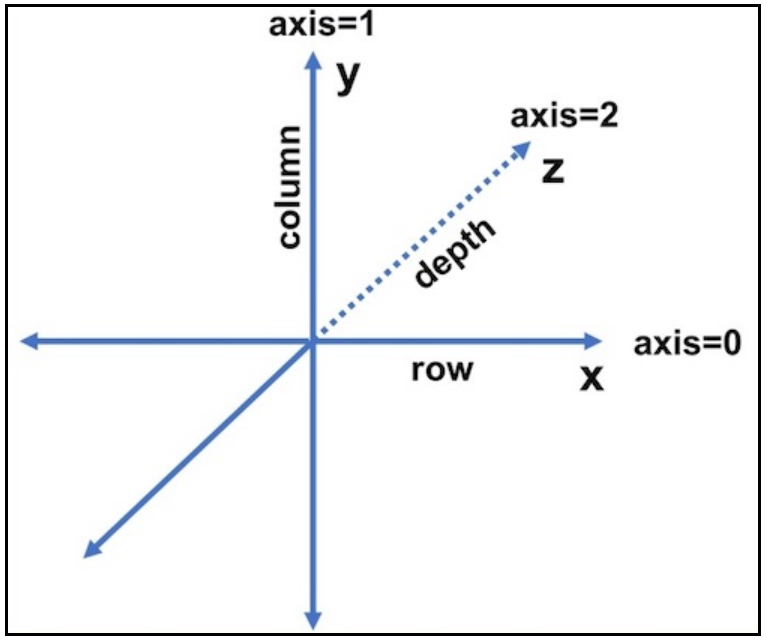
• vector를 위 그림에 적용해보면 vector는 x축만을 가지는 자료형
• 1차원 배열에 해당하는 vector의 각 element는 그 자체가 row

---

• matrix는 x축의 row와 y축의 column을 가짐
• 2차원 배열 matrix는 depth가 1이라고 생각할 수 있음

---

• 3차원 배열 형태의 tensor는 row, column을 가지고 각 column은 vector 형태를 가짐. 이러한 vector를 depth로 표현

---

• 4차원 이상의 배열은 z축의 depth 요소가 scalar가 아닌 vector 이상의 자료형을 가짐을 의미

axis에 따른 np.sum 작동

2-D array

• (row,column) 의 형태
• axis=0은 row 방향, axis=1은 column 방향

# In[1]
x=np.arange(15)
y=x.reshape(3,5)
print(y)

# Out[1]
[[ 0  1  2  3  4]
 [ 5  6  7  8  9]
 [10 11 12 13 14]]

axis=0

# In[2]
t=np.sum(y,axis=0)
print(t)

# Out[2]
[15 18 21 24 27]

• 위의 예에서 15=0+5+10, 18=1+6+11 에 따라 계산되었음.

# In[3]
print(y.shape)
t.shape

# Out[3]
(3, 5)
(5,)

• row를 따라 연산이 이루어졌기 때문에 t.shape은 (5,)가 됨.
• 2-D array data가 1-D vector로 변함.

axis=1

# In[4]
t2=np.sum(y,axis=1)
print(t2)

# Out[4]
[10 35 60]

• 위의 예에서 10=0+1+2+3+4로 계산된 결과

3-D array

# In[5]
z=np.arange(27).reshape(3,3,3)
print(z)

# Out[5]
[[[ 0  1  2]
  [ 3  4  5]
  [ 6  7  8]]

 [[ 9 10 11]
  [12 13 14]
  [15 16 17]]

 [[18 19 20]
  [21 22 23]
  [24 25 26]]]

• 위에서 만들어진 3차원 tensor는 아래와 같이 3행 3열의 데이터가 3개 있다는 것을 의미함.

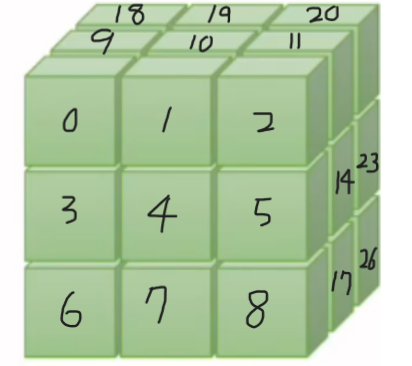
axis=0

• 차원(dimension)을 따라서 압축하는 것으로 생각할 수 있음.

# In[6]
np.sum(z,axis=0)

# Out[6]
array([[27, 30, 33],
       [36, 39, 42],
       [45, 48, 51]])

• 위의 결과에서 27=0+9+18, 30=1+10+19, 33=2+11+20... 에 따라 계산되었음.

axis=1

• 행(row)의 방향에 따라 압축하는 것으로 생각할 수 있음.

# In[7]
np.sum(z,axis=1)

# Out[7]
array([[ 9, 12, 15],
       [36, 39, 42],
       [63, 66, 69]])

• 위의 결과에서 9=0+3+6, 12=1+4+7, 15=2+5+8...에 따라 계산되었음을 확인할 수 있음.

axis=2

• 열(column)을 따라 압축하는 것으로 생각할 수 있음.

# In[8]
np.sum(z,axis=2)

# Out[8]
array([[ 3, 12, 21],
       [30, 39, 48],
       [57, 66, 75]])

• 위의 결과에서 3=0+1+2, 12=3+4+5, 21=6+7+8...에 따라 계산되었음을 확인할 수 있음.

References:
1) https://steadiness-193.tistory.com/46
2) https://steadiness-193.tistory.com/50
3) http://taewan.kim/post/numpy_sum_axis/#case-2-axis-0
4) https://jainkku.tistory.com/27