마르코프 체인 Markov Chain
마르코프 체인이란 (1) 마르코프 성질을 가진 (2) 이산 시간 확률 과정 입니다.
말이 복잡해 보이지만, 현재의 데이터를 기반으로 미래를 예측하기 위한 일종의 조건부 확률로 이루어진 모델링이라고 이해하면 됩니다. 직관적인 예시로 "오늘 습도가 N%이니(현재 데이터) 내일 비가 올 확률은 M%이다(예측)"가 있습니다.
조금 더 쉽게 말하면, 과거의 정보를 가지고 미래의 상태를 확률로 예측할 수 있는 구조라는 뜻입니다.
마르코프 성질 Markov Property
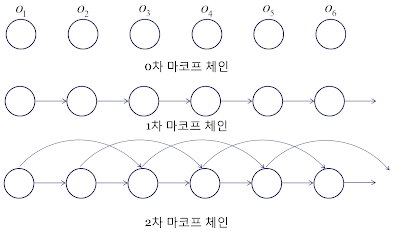
마르코프 성질이란 주어진 시스템의 과거 상태 와 현재 상태 가 주어졌을 때, 미래의 상태 가 현재 상태 에 의해서만 결정된다는 것을 의미합니다. 각 시간 는 이산적으로 변합니다. (시간 단위, 분 단위, ....)
다시 말해, 과거 상태들을 고려한 조건부 확률과 현재 상태만을 고려한 조건부 확률이 동일합니다. 따라서 굳이 과거 상태들을 고려할 필요가 없습니다. 또한 아래와 같이 클러스터링 단위가 바뀌어도 미래의 상태 는 현재 상태 에만 의존합니다.
만약 오늘이 일요일이라면, 지난 주 월요일~토요일까지의 습도 변화를 고려한 내일의 강수 확률과 오늘의 습도만을 고려한 내일의 강수 확률이 같다는 뜻입니다. 화요일~목요일까지의 습도를 고려한 강수 확률과 금요일~일요일까지의 습도를 고려한 강수 확률도 당연히 동일하겠죠.
직관적으로 말해서 현재의 데이터가 과거의 데이터들을 전부 내포하고 있다는 의미입니다.

전이 확률 Transition Probability
전이 확률이란 로 상태가 변화할 확률을 말합니다. 전이 확률을 라고 하면 다음과 같이 표현할 수 있습니다.
각각의 전이 확률을 행렬로 표현할 수도 있습니다. 이를 전이 행렬 Transition Matrix 라고 합니다.
전이 행렬 의 직관적인 의미는 '전체 마르코프 체인의 변화 추이'입니다. 쉽게 말해 전체 시스템이 어떤 상태로 존재할 확률에 대한 표현이라는 의미입니다. 따라서 전이 행렬의 각 row(혹은 col)의 합은 반드시 1이고, 모든 element는 0이상 1이하의 값을 갖습니다.
전이 행렬과 현재 상태를 안다면 전체 마르코프 체인의 상태값을 구할 수 있습니다.
현재 시점을 , 상태 이 분포 (1xM 행렬) 를 따른다고 하면,
는 (1xM) 행렬이고, 는 (MxM) 행렬이므로 위 연산의 결과는 (1xM) 행렬이 됩니다. 즉, n+1 시점의 전이 행렬은 (1xM) 크기의 가 되는 것입니다. 그렇다면 n+2 시점은 어떨까요?
마지막 계산 과정은 의 번째 행과 의 번째 열의 내적과 같습니다. 위 과정을 일반화하면 다음과 같이 나타낼 수 있습니다.
따라서 n+m 시점에서의 분포는 이 됩니다. 즉, 현재 상태의 확률 분포와 전이행렬만 있으면 임의의 시점에서 전체 시스템의 상태를 쉽게 알 수 있습니다.
물론, 이렇게 수식으로 풀어보지 않아도 직관적으로 전이행렬의 거듭제곱으로 미래를 예측할 수 있다는 것을 알 수 있습니다. 왜냐하면 앞서 말한 것처럼 전이행렬은 '마르코프 체인의 변화 추이'이기 때문입니다. 현재 상태의 분포 에 변화 추이를 곱하면 당연히 어떻게 변하는지 알 수 있겠죠. n+2 시점의 상태가 궁금하다면 변화 추이를 두 번 곱해주면 됩니다. 상태가 두 번 변하니까요. 결과적으로 위에서 살펴본 계산 과정과 동일합니다.
정적 분포 Stationary Distribution
그런데 전이행렬의 거듭제곱이라는 건 사실 꽤 많은 계산이 필요합니다. 당장 전이행렬 가 (512, 512) 형태라면 어떨지 상상해보면 감이 오실 겁니다.
그렇다면 일 때는 어떨까요? 만약 이 어떤 극한 분포로 수렴한다면 매번 임의의 시점에서의 상태 정보를 계산하지 않아도 될 것입니다. 그냥 수렴하는 분포를 근사로 사용할 수 있으니까요.
이렇게 수렴하는 어떤 분포 를 정적 분포 Stationary Distribution 라고 합니다. 그리고 이렇게 특정한 분포로 수렴한 상태를 안정 상태, 정상 상태(Steady State) 라고 합니다.
자, 그렇다면 이 어떤 분포로 수렴하는지 아닌지를 어떻게 알 수 있을까요? 간단합니다. 분포 가 다음 조건을 만족하면 됩니다.
만약 가 위 조건을 만족한다면,
와 같이 정리할 수 있기 때문입니다. 그런데 이 연산 과정, 어디서 본 것 같지 않나요?
바로 고유값과 고유벡터의 곱과 같은 형태입니다. 즉, 어떤 마르코프 체인의 정상 상태는 에 대응하는 고유벡터 행렬과 같습니다. 바꿔 말하면 주어진 체인의 전이행렬의 고유값 중 하나는 반드시 1이라는 뜻이기도 합니다.
참고문헌
