
다익스트라 알고리즘은 그래프에서 최단 거리를 구하는 알고리즘
- 출발 노드와 모든 노드 간의 최단 거리 탐색
- 에지는 모두 양수
시간 복잡도 : O(ElogV)
- 인접 리스트로 그래프 구현하기
시간 복잡도 측면 N의 크기가 클 것을 대비해 인접 리스트로 구현하는 것이 좋다 - 최단거리 배열 초기화 하기
최단 거리 배열을 만들고, 출발 노드는 0, 이외의 노드는 무한으로 초기화한다 - 값이 가장 작은 노드 고르기
최단 거리 배열에서 값이 가장 작은 노드를 고른다. - 최단 거리 배열 업데이트 하기
선택된 노드에 연결된 에지의 값을 바탕으로 다른 노드의 값을 업데이트 한다.
Min(선택 노드의 최단 거리 배열의 값 + 에지 가중치, 연결 노드의 최단 거리 배열의 값) - 과정 3~4를 반복해 최단 거리 배열 완성하기
과정 4에서 선택 노드가 될 때마다 가시 선택되지 않도록 방문 배열을 만들어 처리한다.
완성된 배열 = 시작 노드부터 i노드 까지 최단 거릿값 저장
출발 노드와 이외의 모든 노드 간의 최단거리를 표현한다.

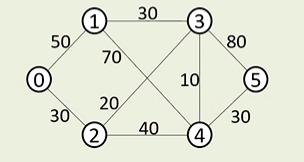
// 모든 정점까지 거리 구하기
public class Main {
static final int INF = 987654321;
static final int MAX_N = 10;
static int N,E;
static int[][] Graph = new int[MAX_N][MAX_N];
static int[] Dist = new int[MAX_N];
static void dijkstra(int src) {
// 우선순위 큐. 람다로 표현 두개값을 비교할때 첫번째 인덱스로 표현하란 의미
PriorityQueue<int[]> pq = new PriorityQueue<>((a,b)->a[0]-b[0]);
boolean[] visited = new boolean[MAX_N];
for(int i=0; i<N; i++) Dist[i] = INF;
Dist[src] = 0;
pq.add(new int[] {0,src});
while(!pq.isEmpty()) {
int[] curr = pq.poll();
int u = curr[1];
if(visited[u]) continue; // 스킵
visited[u] = true;
for(int v=0; v<N; v++) {
if(Dist[v] > Dist[u] + Graph[u][v]) {
Dist[v] = Dist[u]+Graph[u][v];
pq.add(new int[] {Dist[v],v});
}
}
}
}
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
N = sc.nextInt();
E = sc.nextInt();
for(int i = 0; i<N; i++) {
for(int j = 0; j<N; j++) {
if(i==j) Graph[i][j] = 0;
else Graph[i][j] = INF; // 의미상 무한
}
}
for(int i=0; i<E; i++) {
int u = sc.nextInt();
int v = sc.nextInt();
int cost = sc.nextInt();
Graph[u][v] = Graph[v][u] = cost; // 방향성이 없는걸 의미
}
dijkstra(0);
for(int i=0; i<N; i++)
System.out.print(Dist[i] + " "); // 0 50 30 50 60 90
}
} // 경로가 필요한 경우
public class Main {
static final int INF = 987654321;
static final int MAX_N = 10;
static int N,E;
static int[][] Graph = new int[MAX_N][MAX_N];
static int[] Dist = new int[MAX_N];
static int[] Prev = new int[MAX_N];
static void dijkstra(int src) {
PriorityQueue<int[]> pq = new PriorityQueue<>((a,b)->a[0]-b[0]);
boolean[] visited = new boolean[MAX_N];
for(int i=0; i<N; i++) {Prev[i] = -1; Dist[i] = INF;}
Dist[src] = 0;
pq.add(new int[] {0,src});
while(!pq.isEmpty()) {
int[] curr = pq.poll();
int u = curr[1];
if(visited[u]) continue;
visited[u] = true;
for(int v=0; v<N; v++) {
if(Dist[v] > Dist[u] + Graph[u][v]) {
Prev[v] = u; // 정점 바로 전 노드는 u이다 -> 이전노드 저장
Dist[v] = Dist[u]+Graph[u][v]; // 최소비용 저장
pq.add(new int[] {Dist[v],v});
}
}
}
}
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
N = sc.nextInt();
E = sc.nextInt();
for(int i = 0; i<N; i++) {
for(int j = 0; j<N; j++) {
if(i==j) Graph[i][j] = 0;
else Graph[i][j] = INF; // 의미상 무한
}
}
for(int i=0; i<E; i++) {
int u = sc.nextInt();
int v = sc.nextInt();
int cost = sc.nextInt();
Graph[u][v] = Graph[v][u] = cost; // 방향성이 없는걸 의미
}
dijkstra(0);
int curr = 5;
while(curr != -1) {
System.out.print(curr + " < ");
curr = Prev[curr];
}
} // 5 < 4 < 3 < 2 < 0 <- 그리디 알고리즘에 속한다
-매 선택에서 가까운 노드부터 탐색하기 때문에
-음의 가중치는 허용하지 않음. 먼저 방문한 것보다 낮은 비용이 발생할 수 있기 때문에 0 이상의 가중치가 있을때만 다익스트라 사용 가능 - Dynamic programming의 요소를 가진다(DP)
- 새로운 노드까지의 최단 경로를 구하기 위해서 이전에 계산한 결과를 사용 - 최단 경로를 구성하는 부분 경로도 최단 경로이다
// 특정 도착점까지 거리 구하기(2)
public class Main {
static final int INF = 987654321;
static final int MAX_N = 10;
static int N,E;
static int[][] Graph = new int[MAX_N][MAX_N];
static int[] Dist = new int[MAX_N];
static int[] Prev = new int[MAX_N];
static int dijkstra(int src, int dst) { // dst - 도착점. 최단 거리 비용만 반환하기 위해 리턴타입을 int로 변경
PriorityQueue<int[]> pq = new PriorityQueue<>((a,b)->a[0]-b[0]);
boolean[] visited = new boolean[MAX_N];
for(int i=0; i<N; i++) {Prev[i] = -1; Dist[i] = INF;}
Dist[src] = 0;
pq.add(new int[] {0,src});
while(!pq.isEmpty()) {
int[] curr = pq.poll();
int u = curr[1];
if(u==dst) return curr[0]; // 더이상 진행하지 않음. 비용 바로 반환하고 종료
if(visited[u]) continue;
visited[u] = true;
for(int v=0; v<N; v++) {
if(Dist[v] > Dist[u] + Graph[u][v]) {
Dist[v] = Dist[u]+Graph[u][v]; // 최소비용 저장
pq.add(new int[] {Dist[v],v});
}
}
}
return INF; // 무한을 반환함으로써 해당 도착점으로는 갈 수 없다는걸 표현
}
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
N = sc.nextInt();
E = sc.nextInt();
for(int i = 0; i<N; i++) {
for(int j = 0; j<N; j++) {
if(i==j) Graph[i][j] = 0;
else Graph[i][j] = INF; // 의미상 무한
}
}
for(int i=0; i<E; i++) {
int u = sc.nextInt();
int v = sc.nextInt();
int cost = sc.nextInt();
Graph[u][v] = Graph[v][u] = cost; // 방향성이 없는걸 의미
}
for(int i=0; i<N; i++)
System.out.println(dijkstra(0,i));
}
} // 0 50 30 50 60 90