[메모이제이션][DFS] 조합의 경우수

김성수·2023년 4월 28일

DFS 메모이제이션 조합의경우수

알고리즘

목록 보기

8/28

문제 유형

n개의 자연수에서 r개를 뽑아 조합할 때 조합의 경우의 수를 구하시오.

필요자료구조

int n // (자연수 갯수),
int r // (뽑을 갯수),
int[][] fibo // (메모이제이션할 2차원 배열),
DFS() 메서드 // 핵심 로직,

문제 풀이 과정

조합의 공식을 이해해야 한다.

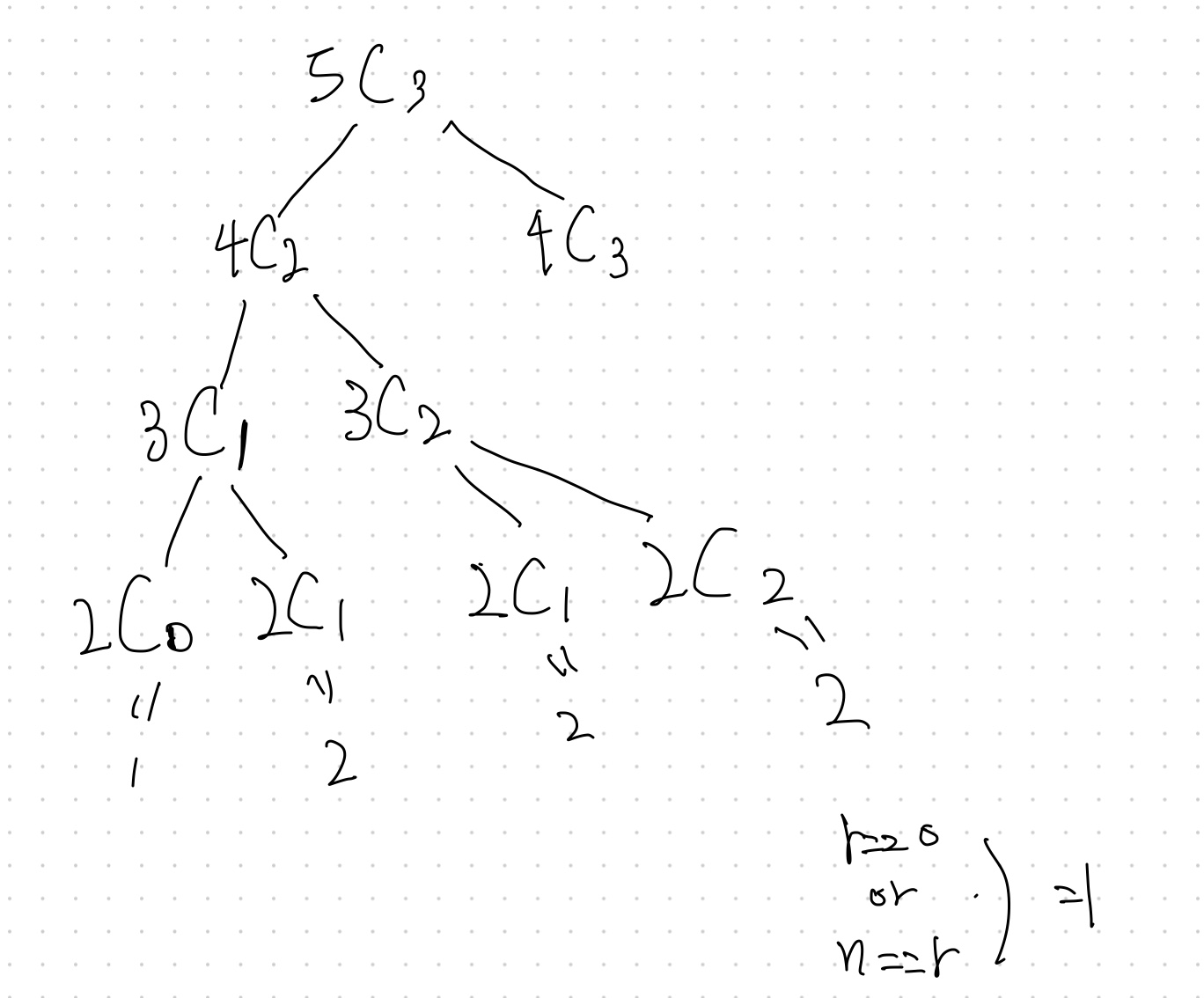
nCr = n-1Cr-1 + n-1Cr

5C3 = 4C2 + 4C3

이유 : 자신의 인덱스를 포함하느냐(o) 포함하지 않느냐(x)를 모두 구한 값이 조합의 경우의 수가 된다.

말이 조금 어렵다.

예를 들어 5개의 자연수 1, 2, 3, 4, 5 집합이 존재할 때,

5라는 값이 포함된다면 4C2 조합의 경우의 수만 구하면 된다.

{1, 2, 5}
{1, 3, 5}
{1, 4, 5}
...

5라는 값이 포함되지 않는다면 4C3 조합의 경우의 수를 구하면 된다.

{1, 2, 3}
{1, 2, 4}
...

조합을 결정할 때 5라는 값은 포함될 수도 있고, 포함되지 않을 수도 있으므로 두 값을 더하면 5C3이 된다.

이를 DFS 알고리즘으로 그린다면 아래 이미지와 같다.

핵심 코드

int[][] fibo = new int[35][35];

public int DFS(int n, int r){
	// fibo 배열에 값이 존재할 때 해당 fibo 출력
	if(fibo[n][r] > 0) return fibo[n][r]; 
	if(n==r || r==0) return 1;
	else return fibo[n][r] = DFS(n-1, r-1) + DFS(n-1, r);
}

개선된 점

문제는 틀렸지만 끝까지 풀어보려고 노력했다!

"이상한 나라의 수학자'에서 최민식 배우 대사 중에 "풀리지 않은 문제가 있을 때 어렵구나, 내일 다시 풀어야지 하는 게 수학적 용기다"

내가 문제가 해결되지 않을 때, 종종 떠올리는 대사이다.

이 대사를 생각하면 복잡한 머리가 조금 차분해지고,

마음의 위안을 얻게되는 것 같다.

피드백, 개선할 점

첫째로 DFS 그래프를 여러 방면으로 그려보는 능력이 부족한 것 같다.

여태까지는 L(레벨)로써 그래프에 접근했지만 이번에는

조합으로써 그래프에 접근했어야 했다.

하지만, 그렇게 접근하지 못했고 4시간 정도 고민했지만 타임리미티드에 걸렸다.

DFS 그래프를 여러 방면으로 그릴 수 있는 능력이 필요해보인다.

느낀점

사실 타임리미티드가 걸려서 문제를 완벽히 해냈다고할 수는 없지만

어느정도 결과를 도출해내는데 성공했다.

이런 유형의 문제를 처음 접해보는 것이기 때문에 고전하는건 당연한거라고 생각한다.

그래도, 끝까지 정답을 보려하지 않고 스스로 패턴을 찾아서 해결하려 했던 내 자신에게 뿌듯함이 있다.

아래는 내가 이 문제를 풀어나갔던 코드이다.


public class 조합의경우수_메모이제이션 {
    static int n;
    static int r;
    static int[] arr;
    static int[] result;
    static int[] ch;
    static int cnt;
    static int answer;


    public void DFS(int L){

        if(L == r){
            for(int i = 0; i < r-1; i++){
                if(result[i] > result[i+1]) return;
            }

            answer++;
//            for(int x : result) System.out.print(x + " ");
//            System.out.println();
        }else{
            for(int i = 1; i <= n; i++){
                if(ch[i] == 0){
                    ch[i] = 1;
                    result[L] = arr[i];
                    DFS(L+1);
                    ch[i] = 0;
                }
            }
        }
    }


    public static void main(String[] args) {
        조합의경우수_메모이제이션 T = new 조합의경우수_메모이제이션();
        Scanner in = new Scanner(System.in);

        n = in.nextInt();
        r = in.nextInt();
        cnt = 0;

        ch = new int[n+1];
        arr = new int[n+1];
//        fibo = new int[10000][r];

        for(int i = 1; i <= n; i++){
            arr[i] = i;
        }

        result = new int[r];

        T.DFS(0);
        System.out.println(answer);
    }
}