https://www.acmicpc.net/problem/30831
문제 요약
- 과목 N개가 주어짐
- 권장 선후수 관계, 필수 선후수 관계가 있음
- 후수과목 : 최대 1개, 필수 선수 과목 : 최대 1개
- 문제에서 주어지는 조건에 따라 과목을 수강
- 필수 과목을 수강하던지
- 후수 과목을 수강하던지
- 수강 안하던지
접근법
- 많이 까다로움
- 간단하게 생각하면
- 강의가 완료된 것은 완료 처리를 함
- 필수 선수 과목을 찾아가면서 수강하지 않은 가장 상위에 있는 것을 찾음
- 후수 과목을 탐색하면서 가장 먼저 나타나는 수강하지 않은 과목을 찾으면 됨
- 이 과정에 시간이 오래 걸리므로 disjoint set의 경로 압축을 적용함
- disjoint set 비슷하게 접근해봄
- 선수든 후수든 여러 과목이 같이 사용할 것이므로
- 후수 과목을 찾아가면서 경로 압축을 시킴
- 약간 다른 점은 후수 과목을 찾다가 강의 완료된 것이 있으면 같이 묶는 처리도 해줌
- 선수 과목도 경로 압축을 시킴
- 필수 선수 과목 : 필수 선수 과목 중 수강하지 않은 가장 상위에 있는 것
- 후수 과목 : 수강한 것중 가장 후 순위에 있는 것
- 필수 선수 과목, 후수 과목만 챙김
- 권장 선수 과목은 필요가 없음
- 서로간에 필수인지 확인가능해야함
- 필수 선수 과목용 관계, 후수 과목용 관계 두 가지를 유지함
- 필수 선수 과목 찾기
- 사전에 필수 과목 끼리는 연결은 해줌 -> 최상위 필수 과목이 부모가 될 것임
- 필수 과목 라인으로 계속 올라감 -> 올라가면서 경로 압축도 해줌
- 필수 선수 과목 처리
- 이미 수강을 했다면? => 필수 과목들은 다 수강했다고 봐도 됨
- 수강을 안했다면? => 수강 처리를 하고 다음번 필수 과목으로 승계해줌
- 다음번 필수 과목 : 지금 수강한 과목의 바로 다음번 필수 과목, 서로 필수 관계여야함
- 지금 과목의 부모를 자식으로 바꿈. 자식의 부모는 자식으로 변경
- 후수 과목 처리
- 일단 수강한 것들의 가장 끝을 찾음
- 가장 끝의 다음 과목이 있는지 확인
- 다음 과목을 수강하는데 이때 중요한 것이, 다음 과목의 필수 선수 과목이 있는지 확인해야함
- 필수 과목이 있으면 : 필수과목 수강
- 필수 과목이 없으면 : 후수 과목 수강. 이때 후수 과목이 누군가의 필수 과목일 수 있음. 이 경우 필수 선수 과목 처리가 필요함
- 예시에서 1을 통해 2를 후수과목으로 처리를 하면 나중에 4나 6은 2번 필수 과목이 이미 수강된 상태가 됨
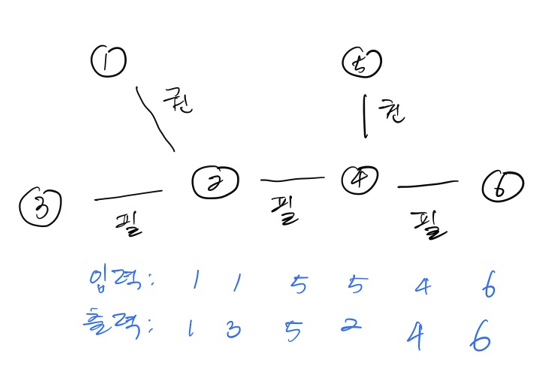
예시
1번 이후에 2번을 수강하면 될 것 같지만 2번의 선수인 3번을 수강해야함