2주차
드디어 2주차도 마무리가 되어 가고 있다. 개인적인 일정들에 강의까지 매일 들으니 조금은 지치는 주간이었지만 그래도 하나씩 배워가고 정리해가는 즐거움이 있는 것 같다. 이번 주차에는 data handling, data analysis와 관련된 강의들이었는데 실질적으로 선형 분석, 회귀 분석들을 통한 예측 단계까지 포함된 강의들은 아니었고, 모델링 전에 데이터를 탐색하는 EDA 과정에서 사용할 법한 방법들을 가르쳐주시는 강의었다. 그 중에서도 통계학입문 수업이나 데이터 분석 관련 과목들을 들으면서 많이 접했지만 헷갈렸던 개념들이 많았던 이변량 분석 파트에 대해서 정리해 보고자 한다. 숫자형, 범주형의 데이터 타입에 따라 어떻게 두 변수간의 관계를 시각화 하는지 그리고 어떤 통계량을 사용해 수치화 하는지 정리해보도록 하겠습니다.
이변량 분석
말 그대로 두개의 변수 간의 관계를 살펴보는 분석을 이변량 분석이라고 할 수 있다. 주로 두 변수간의 관계가 없다는 귀무가설로 두고 대립가설은 두 변수 간의 관계가 존재한다로 두게 된다. 이러한 상태에서 p-value가 유의 수준보다 낮게 나타나면 대립가설을 채택해 두 변수 간의 관계가 있다는 판단을 할 수 있게 된다. 하지만 위에서도 언급했듯
숫자 - 숫자
시각화
숫자 형 변수 간의 관계를 시각화 하는 일반적인 방식은 산점도를 이용하는 것이다.
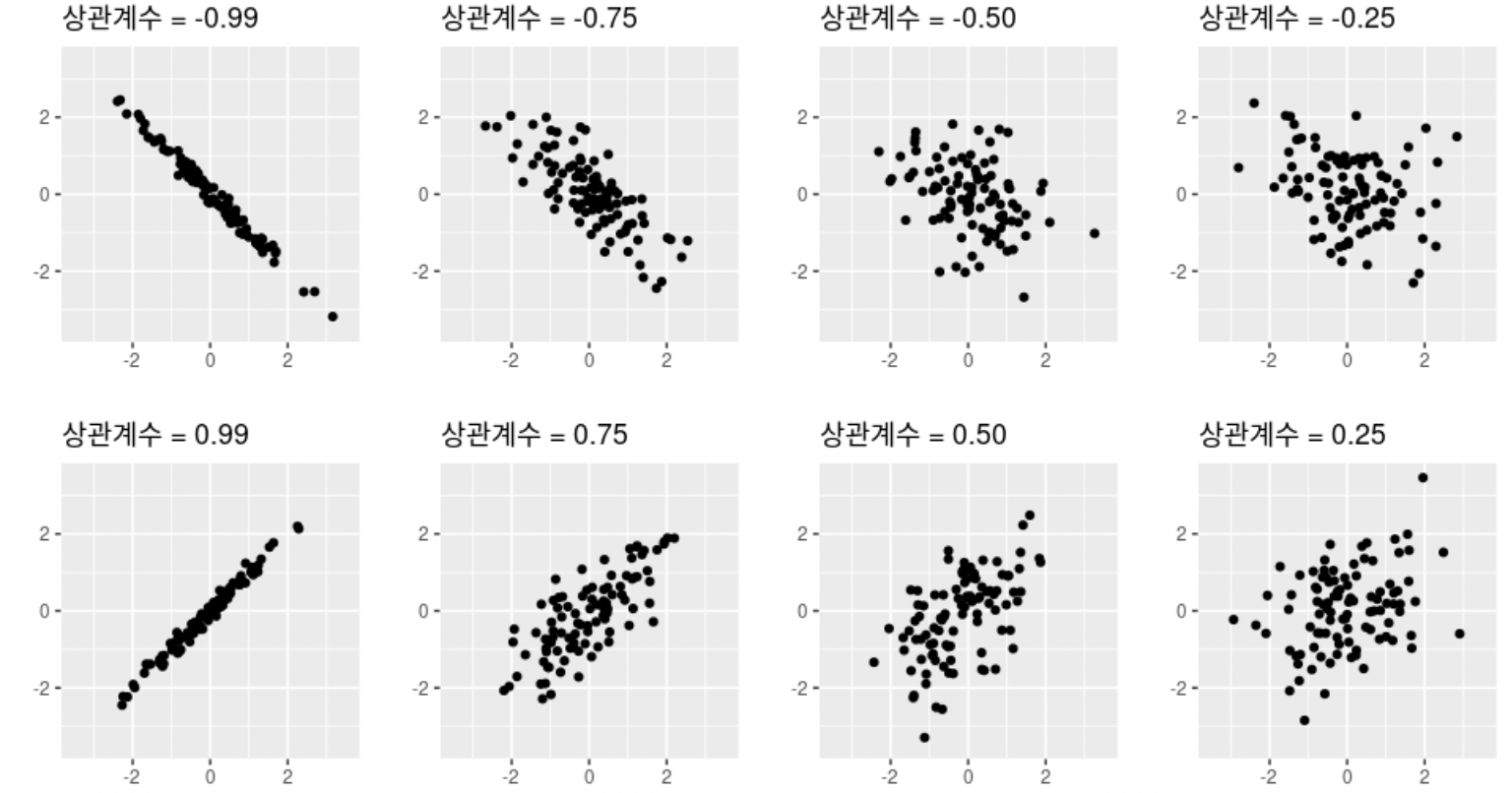
이런 식으로 각 변수 간의 관계를 점을 찍어 표현을 하게 되고, 찍혀진 점들이 얼마나 모여서 선으로 표현되나를 통해 두 변수간의 관계가 얼마나 강한지를 짐작할 수 있게 된다. 해당 그림에서도 보게 되면 이후에 상관 계수에 대해 다루겠지만 상관계수의 절댓값이 높을수록 관계가 강하다라고 볼 수 있는데 상관계수의 절댓값이 높은 그래프들은 직선에 가깝게 나타나고 상관계수의 절댓값이 낮은 그래프들은 형태가 없이 퍼져 있는 것을 볼 수 있다.
plt.scatter(air['Temp'], air['Ozone'])
plt.show()matplotlib의 scatter를 활용하여 쉽게 시각화 할 수 있다.
수치화
위에서도 잠깐 언급 했든 숫자형 변수간의 관계를 수치를 통해 확인할 때에는 상관 계수를 활용한다. 상관계수는 -1 ~ 1 사이의 숫자 값으로 나타나게 되며 상관계수가 양수이면 양의 상관관계, 음수이면 음의 상관관계라고 판단할 수 있다. 여기서 주의할 점은 절댓값이 클수록 상관관계가 크다는 것을 의미하기는 하지만 이것이 관계를 나타낸 직선의 기울기가 커진다는 것을 의미하는 것은 아니다. 산점도를 기준으로 말해보자면 절댓값이 높을수록 점들이 모여있는 모양이 직선에 가깝다는 것만을 의미하는 것이다.
spst.pearsonr(air['Temp'], air['Ozone'])
>> (0.6833717, 2.1977698e-22)scipy패키지를 활용하여 쉽게 상관계수를 얻어 낼 수 있다. 물론 상관계수를 계산하는 수식 또한 존재하지만 본 포스트에서는 수식을 통한 이해가 더 쉬운 경우가 아니라면 수식을 다루지 않도록 하려고 한다. 하여튼 해당 코드를 통해 계산을 하면 저렇게 두개의 숫자가 나오게 되는데 앞의 숫자가 상관계수, 뒤의 숫자가 p-value이다. 저 두 숫자를 통해서 그래프에서 명확하지 않았던 두 변수간의 관계를 파악할 수 있다.
한계점
상관계수의 경우 선형적인 관계만을 표현할 수 있다는 한계가 있다. 하지만 비선형적인 경우 그 불확실성 때문에 수치화하는 경우가 잘 없고, 수치화를 하려면 대부분 상관계수를 통해 판단한다고 볼 수 있다.
범주 - 숫자
시각화
범주형 변수를 x로 두고 숫자형 변수를 y로 두어 두 변수 간의 관계를 파악할 때는 평균비교 barplot을 활용하게 된다.

위의 그림에서처럼 각 범주별로 해당 숫자형 변수의 평균을 계산하여 barplot으로 그려낸 것이라고 할 수 있다. 각 그래프 bar 가운데에 있는 검은색 선은 신뢰구간을 의미하고 그래프를 통해서 관측했을 때 평균 간의 차이가 크고, 신뢰구간이 겹치지 않을 때, 대립가설을 채택해 범주형 변수간의 차이가 존재한다고 파악할 수 있다.
sns.barplot()을 활용하면 다른 그래프 그리는 명령어와 크게 다르지 않다.
수치화
범주 - 숫자 형 변수의 관계에서는 두가지 통계량을 활용하게 된다. 범주형 변수가 2개일 때와 그 이상일 때를 나누어 활용할 수 있다.
t-통계량
두 그룹의 평균 간 차이를 표준오차로 나눈 값이다. 하지만 사실상 분석에서는 두 평균의 차이라고 이해해도 좋다. t 통계량의 절댓값이 클수록 두 평균 간의 차이가 크다고 이해해도 된다는 뜻이다.
temp = titani.loc[titanic['Age'].notnull()]
died = temp.loc[temp['Survived'] == 0, 'Age']
survived = temp.loc[temp['Survived'] == 1, 'Age']
spst.ttest_ind(died, survived)t-test의 경우 본 데이터를 내가 사용하고 싶은 변수들만 따로 뽑아서 활용해야 하기에 코드에서의 약간의 차이가 존재한다. 위의 코드를 참조하자.
통상적으로 t-통계량의 절댓값이 2보다 크게 나타나면 두 변수 간의 유의미한 관계가 있다고 판단할 수 있다.
ANOVA
만약 범주 형 변수의 범주가 3개 이상이라면 anova테스트를 활용하게 된다. ANalysis Of VAriance 의 줄임말로 분산 분석이다. 이전에 통계학입문을 통해서 공부했을 때 이 지점이 가장 이해가 되지 않았다. 결과적으로 각 범주간의 평균을 비교하고 싶을 때 왜 분산 분석을 활용하는 것인지에 대한 이해가 되지 않았던 것이다. 하지만 이 분석이 집단 간 분산을 집단 내 분산으로 나눈다는 것을 알게 되면 조금 이해가 된다. F 통계량이라고 칭하게 되고, 각 범주의 그룹 간 분산이 각 집단 내에서의 분산보다 크면 각 집단 간의 차이가 존재한다고 판단할 수 있는 것이다.
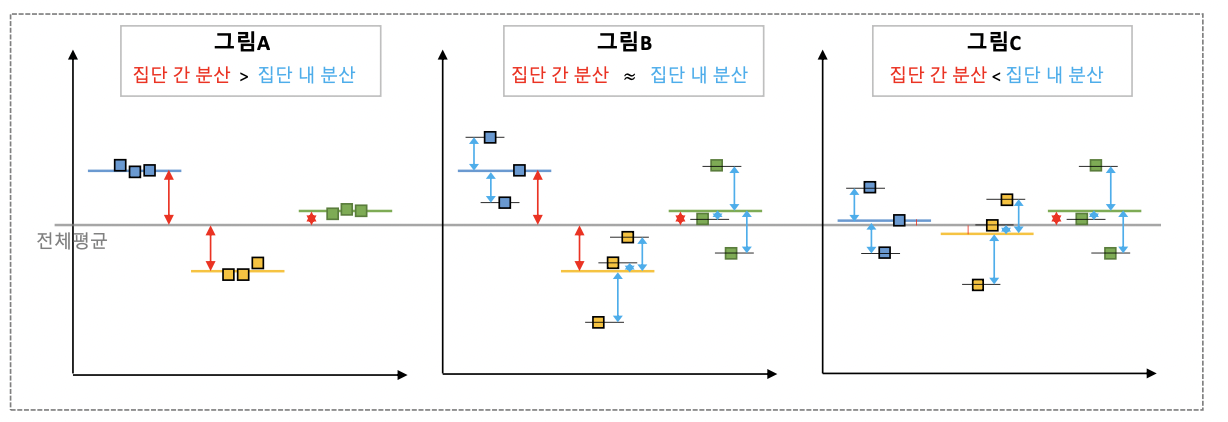
위 그림을 보고 다시 한번 위의 설명을 보면 조금 더 이해가 편할 것 같다.
anova테스트 또한 그룹 별로 따로 저장을 한 후 spst.f_oneway()를 활용하여 f-통계량을 얻을 수 있다. 하지만 어느 그룹 간에서 차이가 있는지는 알 수 없기 때문에 차이가 있다는 통계량이 나온다면 보통 사후분석을 진행하게 된다.
범주 - 범주
시각화
범주형 변수와 범주형 변수 간의 관계는 모자이크 플롯이라는 시각화 방법을 활용할 수 있지만, 수치 간의 차이가 클 때에는 crosstab(교차표) 또한 활용하여 볼 수도 있다. 하지만 교차표의 경우에는 엑셀에서도 많이 접하기 때문에 모자이크 플롯을 위주로 살펴보도록 하자.
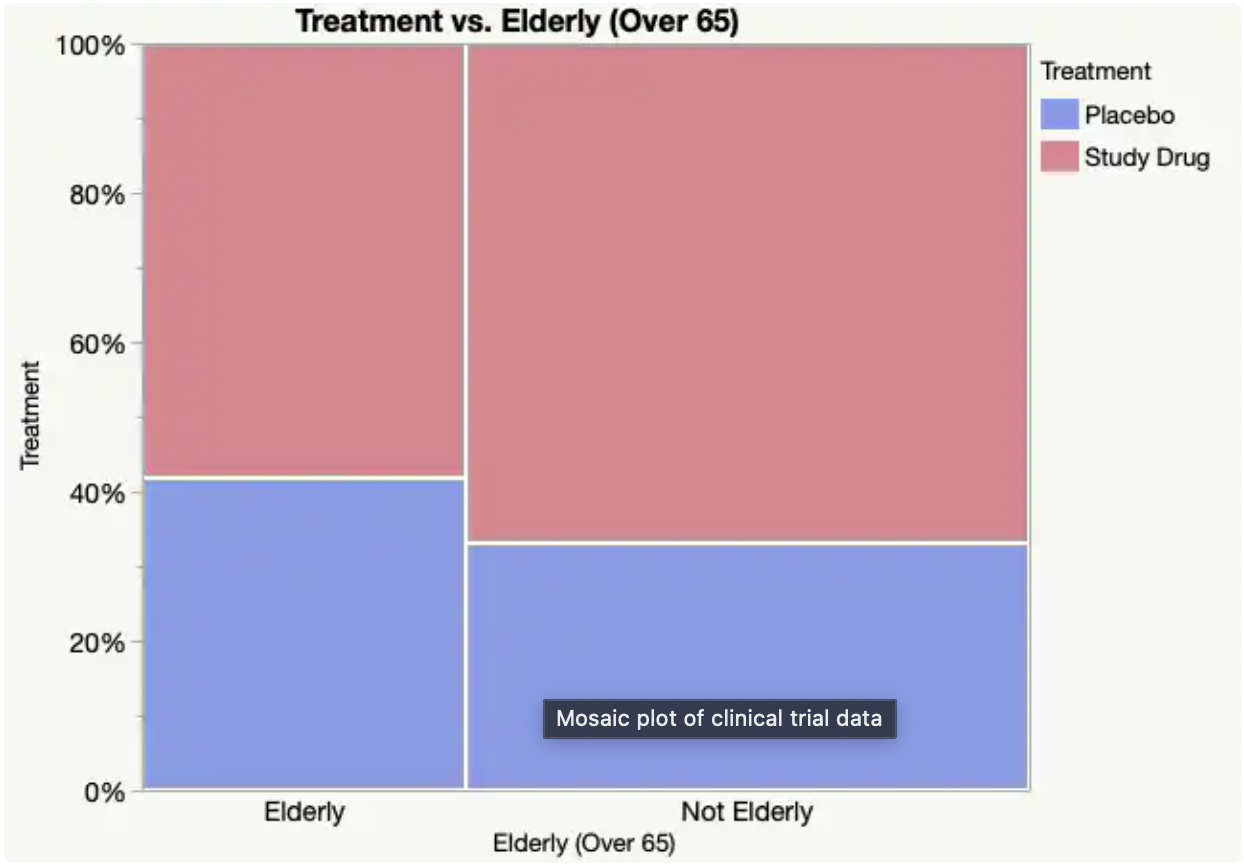
위 그래프는 x범주의 변수에 대한 y범주의 갯수를 비율로 나타낸 것이라고 할 수 있다. 즉 countplot을 기반으로 표현된 그래프라고 할 수 있다. 즉 각 범주별로 비율의 차이가 나타나는지를 파악할 수 있다.
mosaic(titanic, ['Pclass', 'Survived'])모자이크 플롯의 경우 matplotlib이나 seaborn패키지와는 약간은 사용법이 다르기 때문에 모자이크 플롯도 위의 코드를 참고해보자.
수치화
범주형 변수 간의 관계에서는 카이제곱 분포를 활용한다. 카이제곱 분포를 조금 더 잘 이해하기 위해서는 기대빈도에 대한 이해가 필요하다. 기대빈도는 범주 간의 아무런 관련이 없을 때 나올 수 있는 빈도수를 의미한다. 그리고 카이제곱 통계량은 관측빈도와 기대빈도간의 차이를 수치화하여 나타낸다. 이렇게 나온 통계량이 자유도의 약 2배보다 크면 차이가 있다고 판단할 수 있다. 자유도에 대해서도 조금 더 깊은 이해가 있다면 좋겠지만 여기서는 (x변수의 개수 -1) * (y변수의 개수 - 1)을 활용해도 좋다.
숫자 - 범주
시각화
숫자 - 범주 형의 관계에서는 kdeplot을 활용할 수 있다. 사실 kdeplot은 밀도함수를 그려주는 기능이기 때문에 단변량 분석에서도 활용된다. 하지만 hue 옵션을 통해 관측하고 싶은 y변수의 값에 따라 다른 그래프를 그려주면서 두 그래프의 비교를 통해 차이를 분석할 수 있다.
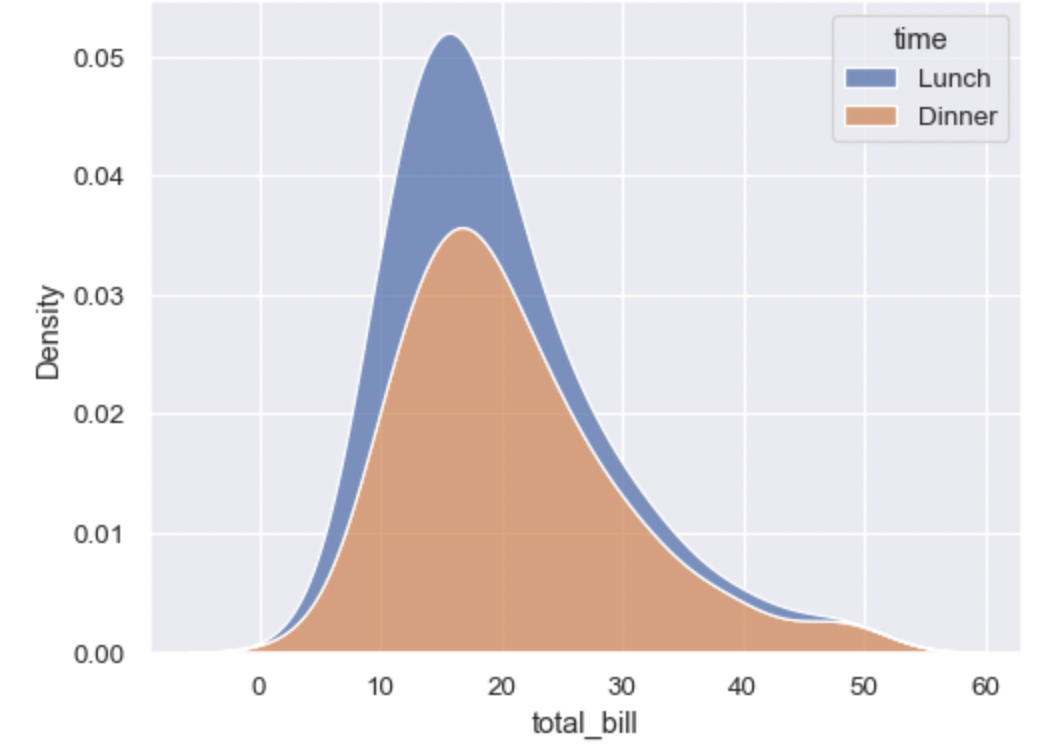
옵션에 따라 조금씩 다르게 나타나겠지만 전체적인 모양은 위와 유사한 그래프가 나오게 된다. 그리고 두 그래프가 많이 겹쳐있지 않을 수록 변수 간의 관게가 크다고 판단할 수 있다.
2주차 정리
이렇게 이변량 분석과 함께 단변량 분석을 이번주 동안 다루게 되었고, 앞으로의 프로젝트에서도 eda에서 많이 활용해 볼 수 있을 것 같다.