2. 시간 복잡도

너스레:)·2023년 7월 24일

Algorithm-Python

목록 보기

2/2

2.1. 시간 복잡도란?

더 나은 알고리즘을 판단하는 기준
복잡도
- 시간 복잡도
- 공간 복잡도

가장 먼저, 제시된 제한 시간과 메모리 사용량을 확인한 후에, 조건에 맞게 실행되도록 문제를 풀어야 한다.

프로그래머스의 경우, 제한시간이 일반적으로 10초임.

2.1.1. 빅오(Big-O) 표기법

Big-O 표기법 : 점근 표기법 中 점근적 상한 표기법
결국엔 최고차항만 남는다
- 상대적으로 나머지 연산은 너무 작아 무시 가능

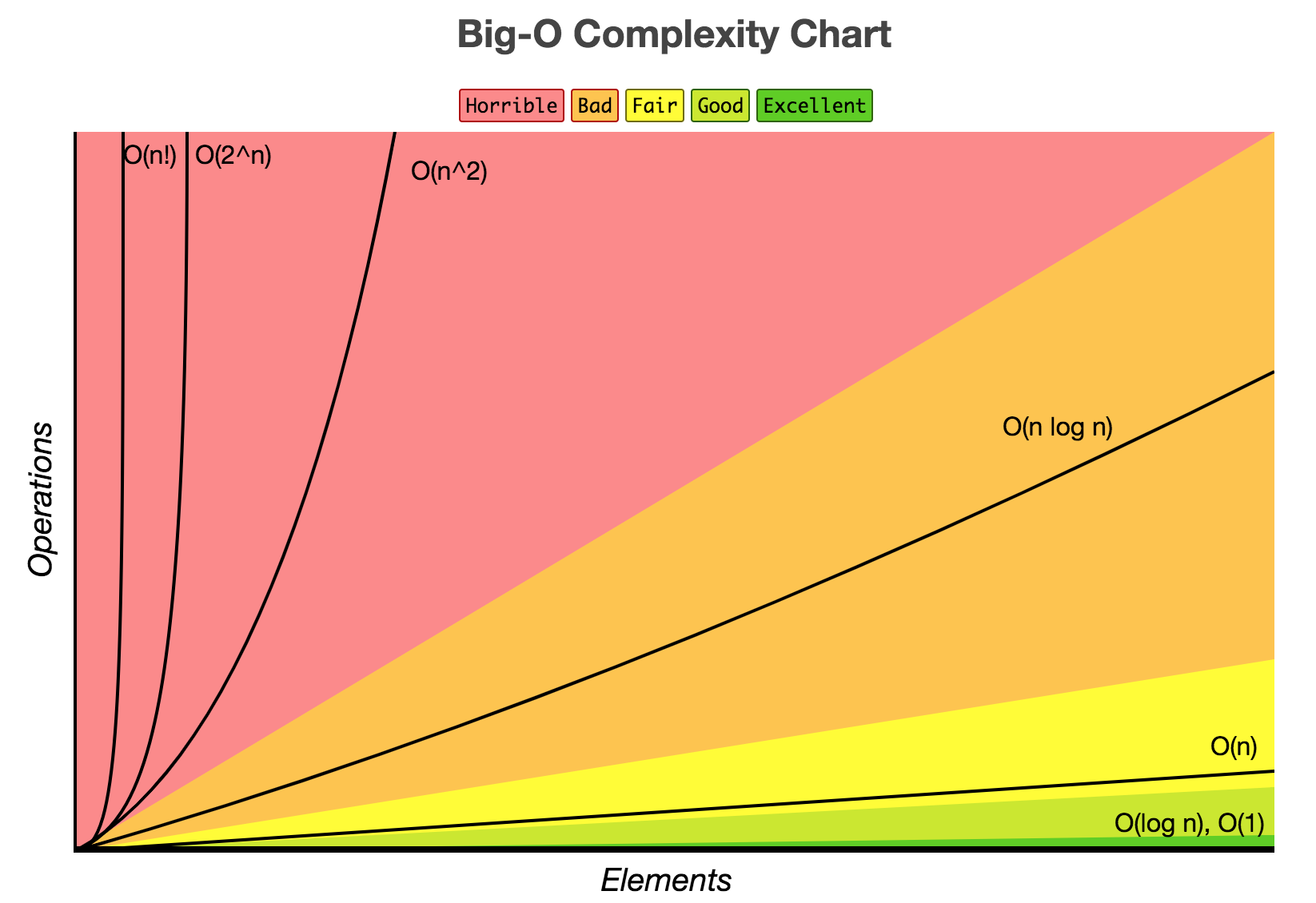
2.1.2. 시간 복잡도의 그래프

1 < log(n) < n < nlog(n) < n^2 < 2^n < n!

컴퓨터는 대략 1초에 1억 번 연산한다.
- Why?
☞ CPU가 1초에 1억 번 연산하기 때문.
☞ 만약 컴퓨터나 CPU의 성능이 여기서 더 좋아진다고 하더라도, 요즘 출제는 근본적인 알고리즘 자체가 틀리면 아무리 코드를 최적화한다고 해도 통과할 수 없도록 출제하고 있음.

따라서 입력 데이터와 연산 횟수를 미리 고려해서, 시간 제한을 넘기지 않는 알고리즘을 처음부터 잘 선택하는 것이 중요!

cf) 각 시간 복잡도의 개념 & 사용되는 상황

2.1.3. 시간 복잡도 선택 시 참고사항

시간 복잡도를 먼저 고려하여, 불가능한 시간 복잡도의 방법은 과감하게 배제하는 식으로 풀이시간 줄일 것.

ⓐ 입력 데이터 수에 따른 시간 복잡도 (기준: 1초)

1천 개 ☞ O(n^2) 이하
1만 개 ☞ O(n^2) 미만
10만 개 ☞ O(nlog(n)) 이하
100만 개 ☞ O(nlog(n)) 미만
그 이상 ☞ 아예 특정 알고리즘을 사용하도록 요구하는 문제일 가능성 ↑. 문제 조건 유심히 확인할 것.

ⓑ 자료구조에 따른 시간 복잡도

자료구조	탐색	삽입	삭제
배열	O(n)	O(n)	O(n)
정렬된 배열	O(log(n))	O(n)	O(n)
연결 리스트	O(n)	O(1)	O(1)
스택/큐	O(n)	O(1)	O(1)
해시	O(1)	O(1)	O(1)
이진 트리	O(log(n))	O(log(n))	O(log(n))

2.2. 시간 복잡도의 계산

2.2.1. 시간 복잡도_어림짐작 해보기

계산이 고정된 횟수 이내로 끝난다면, 반복문이나 좀 복잡한 연산을 했더라도 섣부르게 O(n^2)라고 단정 지을 필요 없음.
즉, 입력 데이터 수에 따라 정말 해당 시간 복잡도가 나오는 것이 맞나 체크해볼 것.

빅오 표기법
☞ 시간 복잡도에 대해 빠르게 감을 잡기 위함이지, 정확하게 측정하고자 함이 아니다.

cf) 내장 함수의 시간 복잡도

자주 사용하는 내장 함수 (3가지)
: 리스트, 집합, 딕셔너리

https://wiki.python.org/moin/TimeComplexity

가장 오래 걸리는 작업 또는 라이브러리 함수의 시간 복잡도를 우선 계산하고,
추가로 연산이 발생하는 곳을 탐색하는 방향으로
전체 시간 복잡도에 대한 감을 잡는 것이 좋다.

2.2.2. 시간 복잡도_줄이는 방법

ⓐ readline() 함수 ☞ '입력 속도' 줄이기

import sys

data = sys.stdin.readline()

입력값을 받는 코드도 직접 구현을 해야하는 경우
받은 문자열을 다시 쪼개더라도, input() 함수보다는 sys 모듈의 readline() 함수를 이용하는 게 훨씬 효율적이다!

ⓑ 리스트 곱셈 ☞ 빠른 '초기화 & 할당'

data1 = [0 for _ in range(1000)]	# O(n)

data2 = [0] * 1000					# O(nk) // 권장

미리 할당해놓은 '고정' 배열을 다뤄야하는 경우
(보통 '리스트'는 '동적'으로 다루는 게 일반적이긴 함)

ⓒ 문자열 붙이기 ☞ YES : ''.join() / NOPE : +

Q. 왜 문자열들을 붙일 때, +를 사용하면 안 되는가?
A. 파이썬에서 문자열(str)은 'immutable'이기 때문이다.
따라서 +을 사용할 경우, 각각의 문자열을 새로운 메모리에 복사해서 새 문자열을 만들기 때문에, 사실상 그 시간 복잡도가 O(n^2)이 되어버린다.

그러니까 문자열을 붙이고 싶다면, ''.join() 을 사용하자!

► immutable 이란?
An object with fixed value.
Immutable objects include numbers, strings and tuples.
Such an object cannot be altered. A new object has to be created if a different value has to be stored. They play an important role in places where a constant hash value is needed such as the keys of a dictionary.

ⓓ 조건문의 연산 줄이기 ☞ '더 짧은' 조건을 '더 앞쪽에' 배치

다중 조건의 경우,

and ☞ 앞쪽 조건이 False라면
or ☞ 앞쪽 조건이 True라면

그 뒤쪽 조건은 계산하지 않고 바로 결과를 도출한다.

ⓔ 슬라이싱 ☞ 불필요한 연산 줄이기

파이썬의 특별한 기능
슬라이싱을 통해, 하나의 변수를 최대한 활용하여 많은 불필요한 코드를 줄일 수 있음
Where to 적용? ☞ 연속된(iterable) 자료형 ; 리스트, 튜플, 문자열 등
for 문에도 활용 가능
주의할 점 : a[start : end : step] 에서 end는 포함 X
'음수' 인덱스

data = [[(0, 1), (2, 3), (4, 5)], [(6, 7), (8, 9), (0, 1)]]
print(data[1:][0][::2])

'''
결과값

[(6, 7), (0, 1)]
'''

'리스트'를 슬라이싱 했다면, 결과값도 '리스트' 형태로 나옴

ⓕ 표준 라이브러리의 활용 ☞ 안전성 & 속도 모두 잡기

어떤 언어를 사용하든 간에, 언어별 기본 특성 & 유용한 라이브러리는 반드시 파악해둘 것
지금 이 코드를 '직접' 구현하는 게 정말 맞나;
즉, 이미 검증을 마친 '표준 라이브러리'에 손쉽게 맡길 순 없는가 다시 한 번 생각해볼 것
표준이 아닌 '외부' 라이브러리의 사용은 지양

# 자주 사용하는 표준 라이브러리

heapq
- 이진 트리 기반의 최소 힙 자료구조
- 항상 정렬된 상태에서 값 추가/삭제
- 우선순위 큐, 최단 거리 알고리즘
collections
- counter
  - 연속된 자료형에서 동일한 원소가 몇 개 있는지 확인 가능
  - 해시 문제
- deque
itertools
- 경우의 수 문제
  - 순열(permutations), 조합(combinations), 중복순열(permutations_with_replacement), 중복조합(combinations_with_replacement)
math
- 수학 문제
  - 최대공약수, 최소공배수, 팩토리얼, 제곱근, 로그, 상수(파이, 자연상수) 등
bisect
- 이진 탐색 기능
  - 정렬된 데이터의 특정 범위 안에 원소가 있는지, 몇 개가 존재하는지 확인

ⓖ (리스트) 컴프리헨션 vs. 제너레이터 ☞ 편의성 vs. 효율성

# (리스트) 컴프리헨션

<장점>

[ 선언 → 할당 → 재구성 ]의 과정을 단 한 줄에 모두 끝낼 수 있는 편의성 有
적용가능한 자료형 : 리스트(多) + tuple, set, dict 등
if 문의 중첩 ⇒ "and" 로 취급함

[i for i in range(11) if i % 2 == 0 if i % 5 == 0]

<단점>

공간 복잡도의 고려 必
- 컴프리헨션은 데이터가 10만 개, 100만 개 있을 때, 정말 그 데이터들을 모두 생성하기 때문
- 편리한 기능은 대부분 공간 복잡도의 문제가 발생하는 경우가 많음..
너무 과도한 컴프리헨션은 이해를 어렵게 해 오히려 큰 문제를 일으킴

# 제너레이터

Q. '제너레이터'란?
A. 연속 가능한(iterator) 자료형을 반환하는 함수.

'한 번에 함수 모두 실행 & return으로 결과값 반환' (X)

'함수가 실행되었다가 다음 next()를 대기하면서 실행이 멈춤 & yield로 결과값 반환' (O)

cf) 제너레이터 만드는 방법 (2가지)
i. 함수 정의 시, return 대신 'yield' 작성
ii. 컴프리헨션 문구를 '소괄호 ()'로 감싸줌