개념
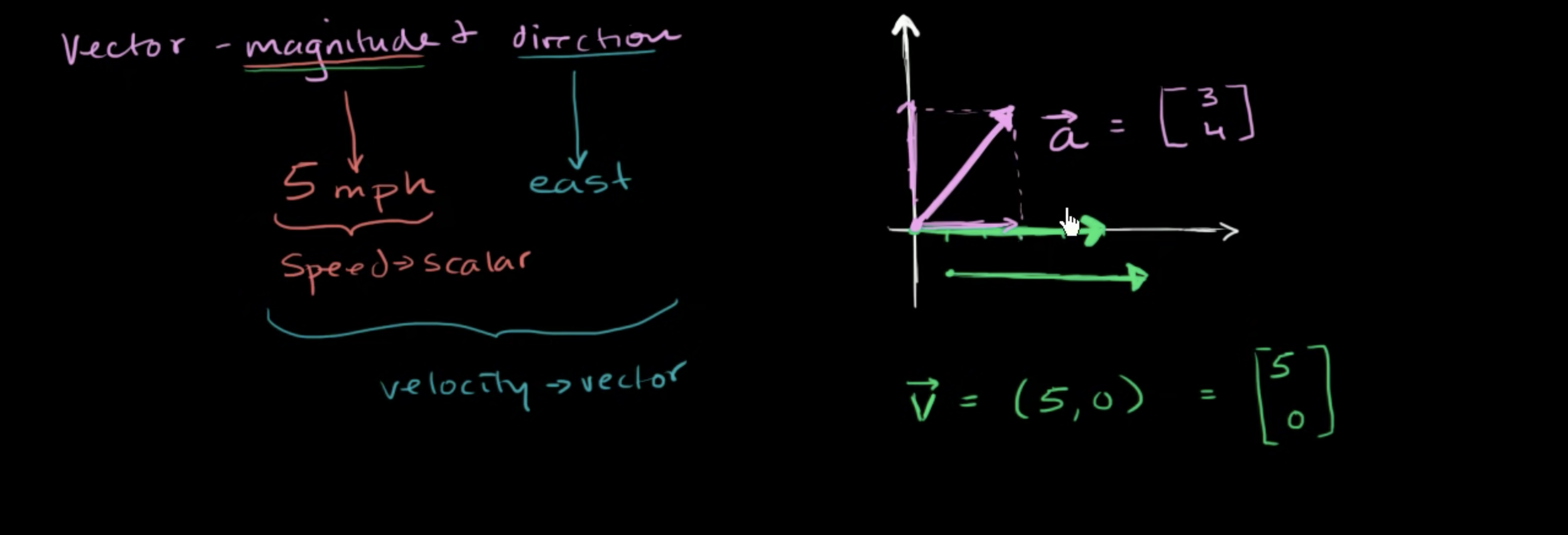
-
5mph : - refer as
speed-> scalar -
5mph + east - refer as
velocity-> vector -
don't care about start point
-
only mganitude + direction
실좌표공간 (real coordinate space)

- 차원이 올라가면서 그래프만으로 표현하기에는 한계가 있기 때문에 표현방식을 정의
-R ^ n - n차원의 실좌표공간 의미 : n차원의 가능한 모든 좌표의 조합
벡터의 합 (차)
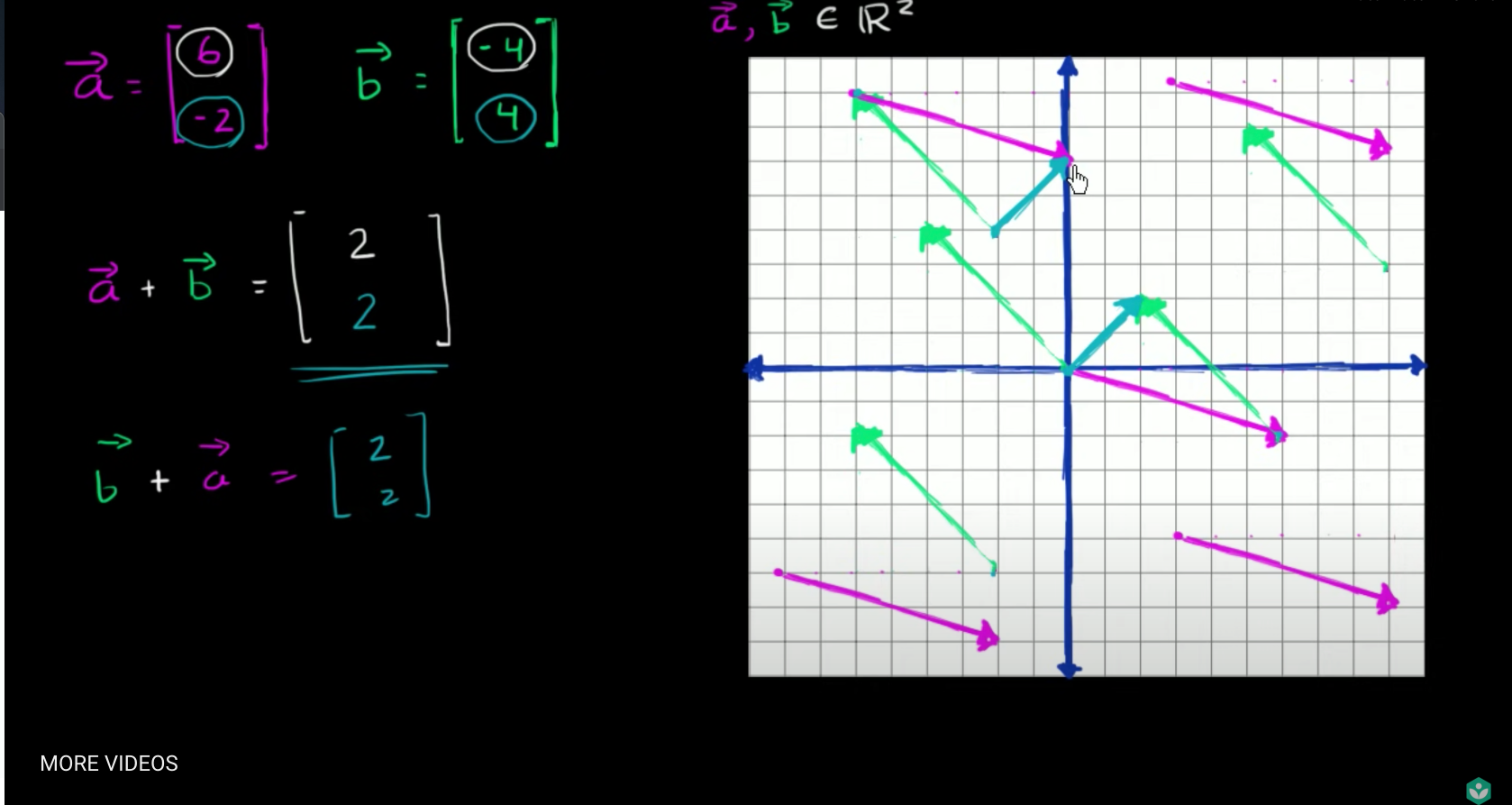
- 두 벡터의 합은 첫번째 벡터의 끝 점에서 다른 벡터를 시작했을 때 끝나는 지점이다.
- 이 합은 각 component간의 합에 해당하는 벡터를 첫번째 벡터의 시작점에서 이동한 것과 동일하다.
- 교환법칙이 성립된다.
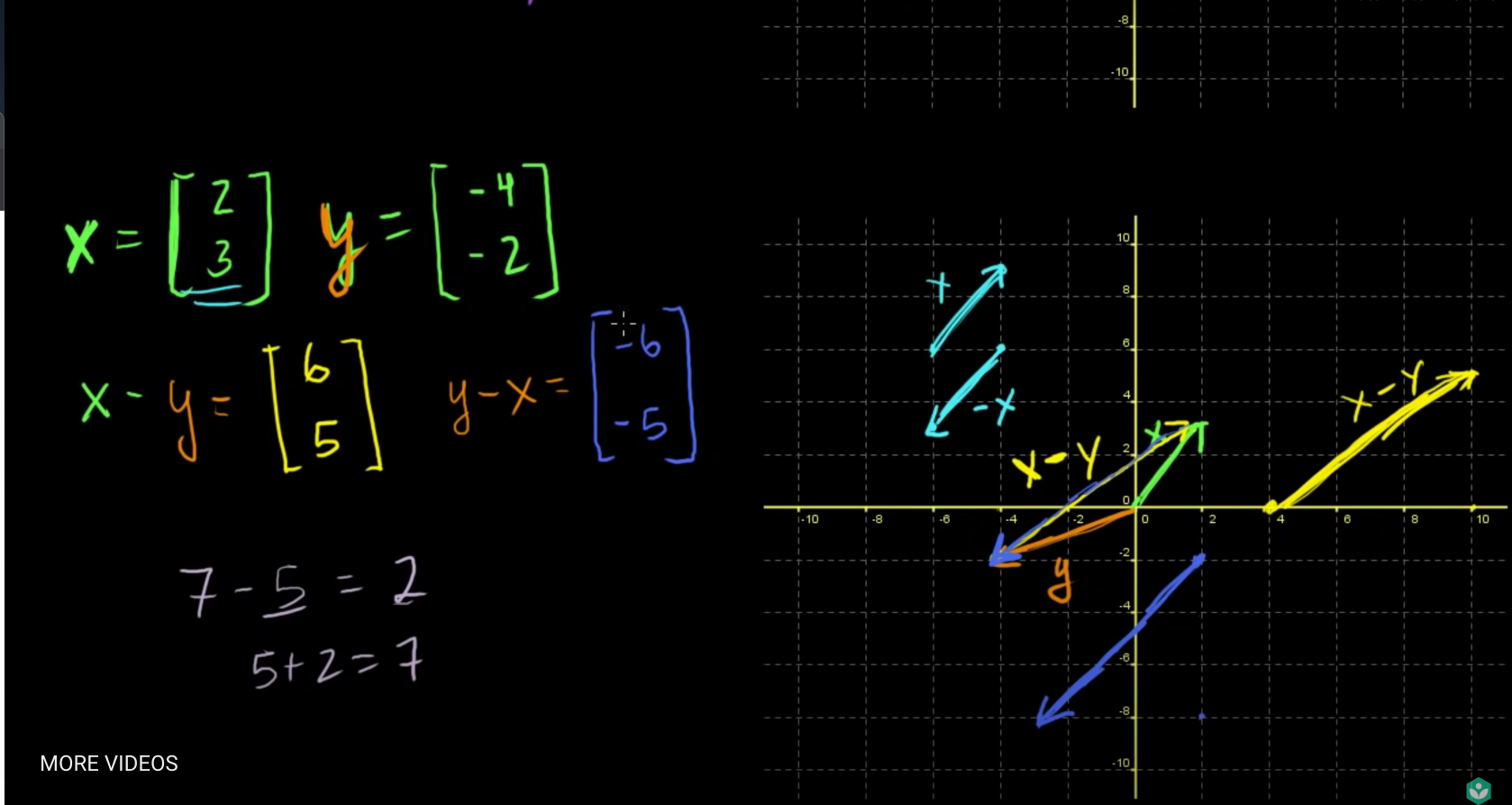
- 두 벡터의 차도 논리는 같음
- 다만 벡터의 차는 교환법칙이 성립되지 않는다.
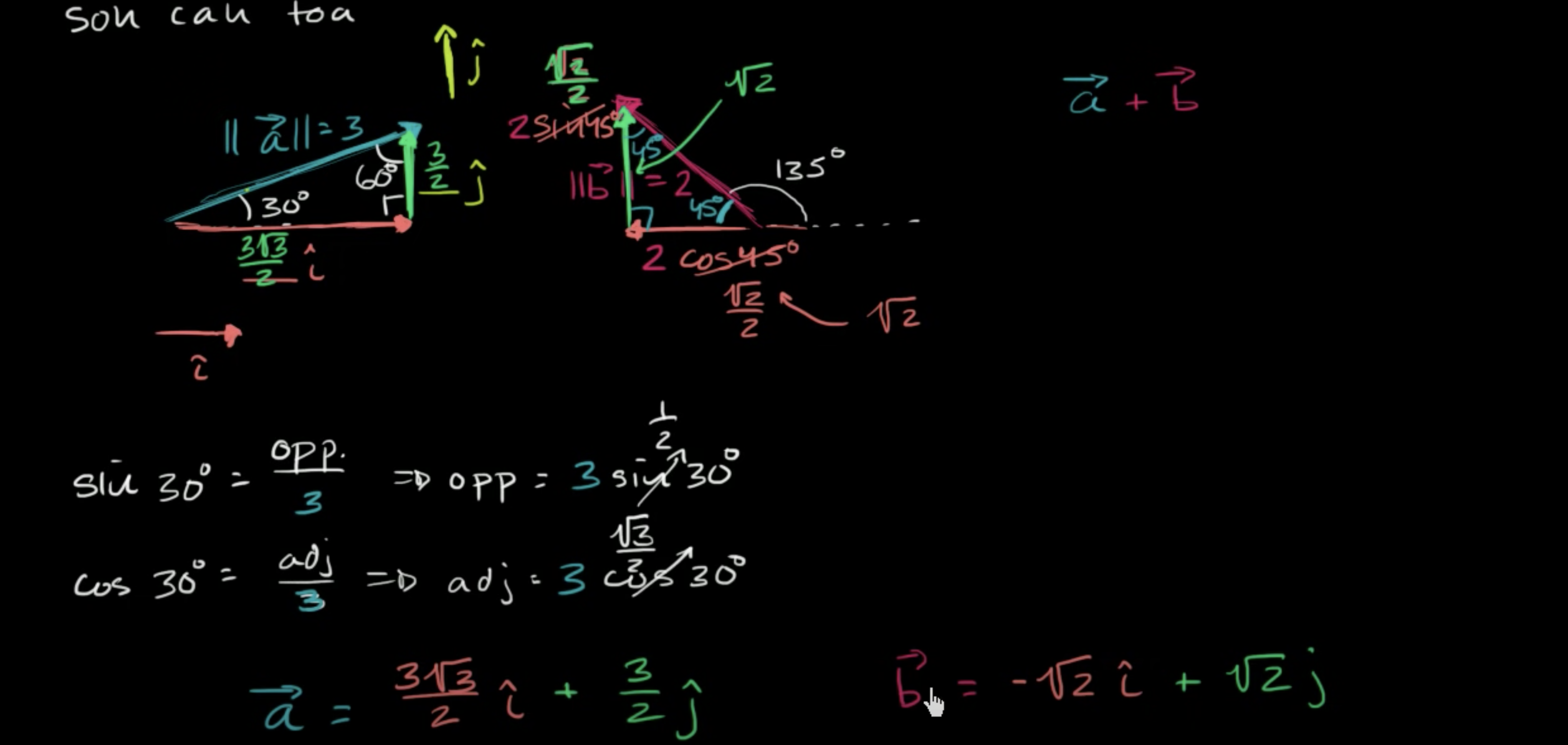
- magnitude를
삼각형의 빗면이라 생각 - θ를 통해서 방향성을 표현
ex θ = 45 -> + // θ = 225 -> - 삼각함수를 통해서 벡터의 좌표를 구할 수 있음.png)
벡터와 스칼라의 곱
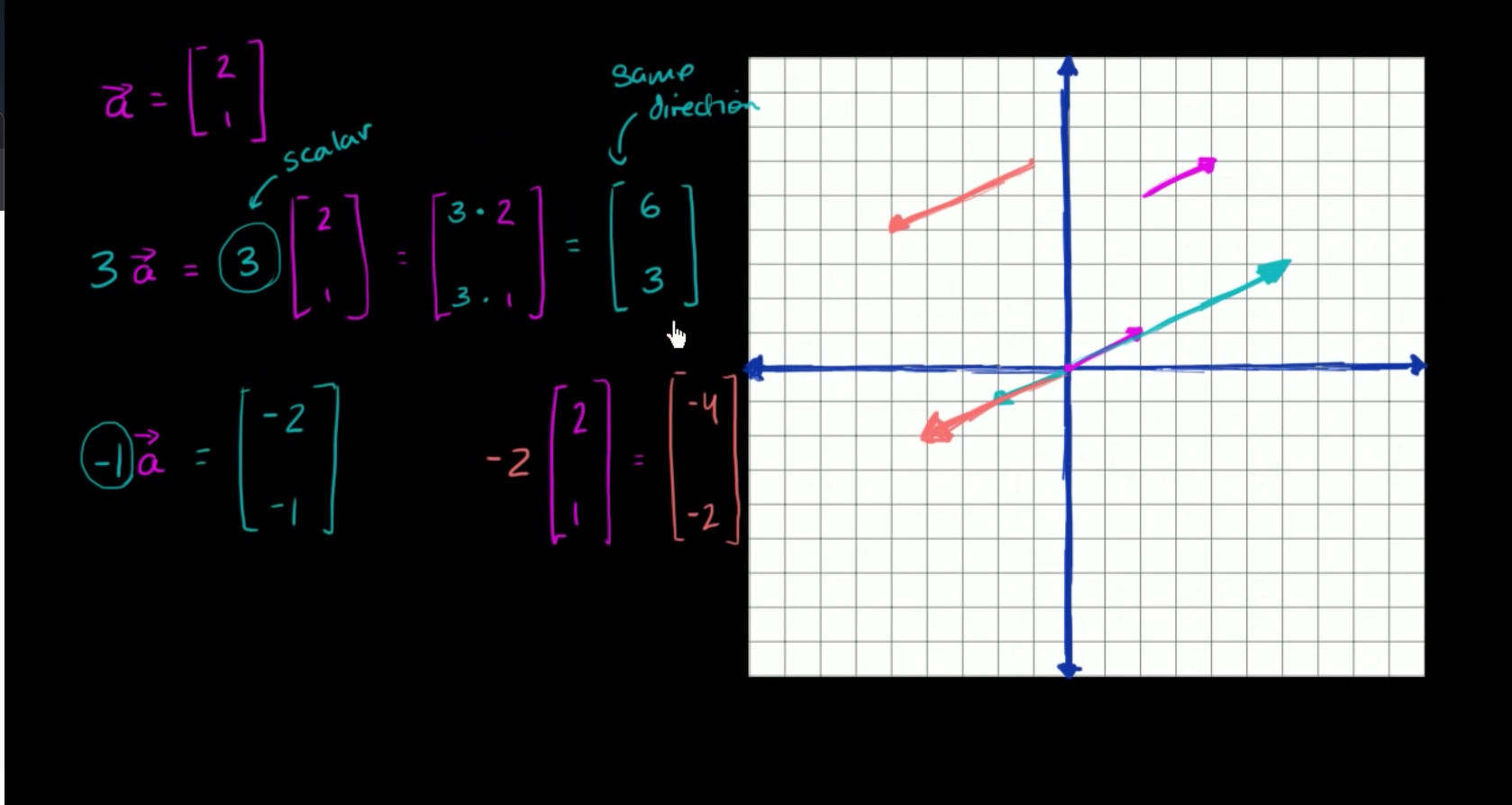
양수 scala 곱 (3*vector)
- same direction
- change magnitude
음수 scala 곱 (-2*vector)
- change direction
- change magnitude
단위벡터 (unit vector)
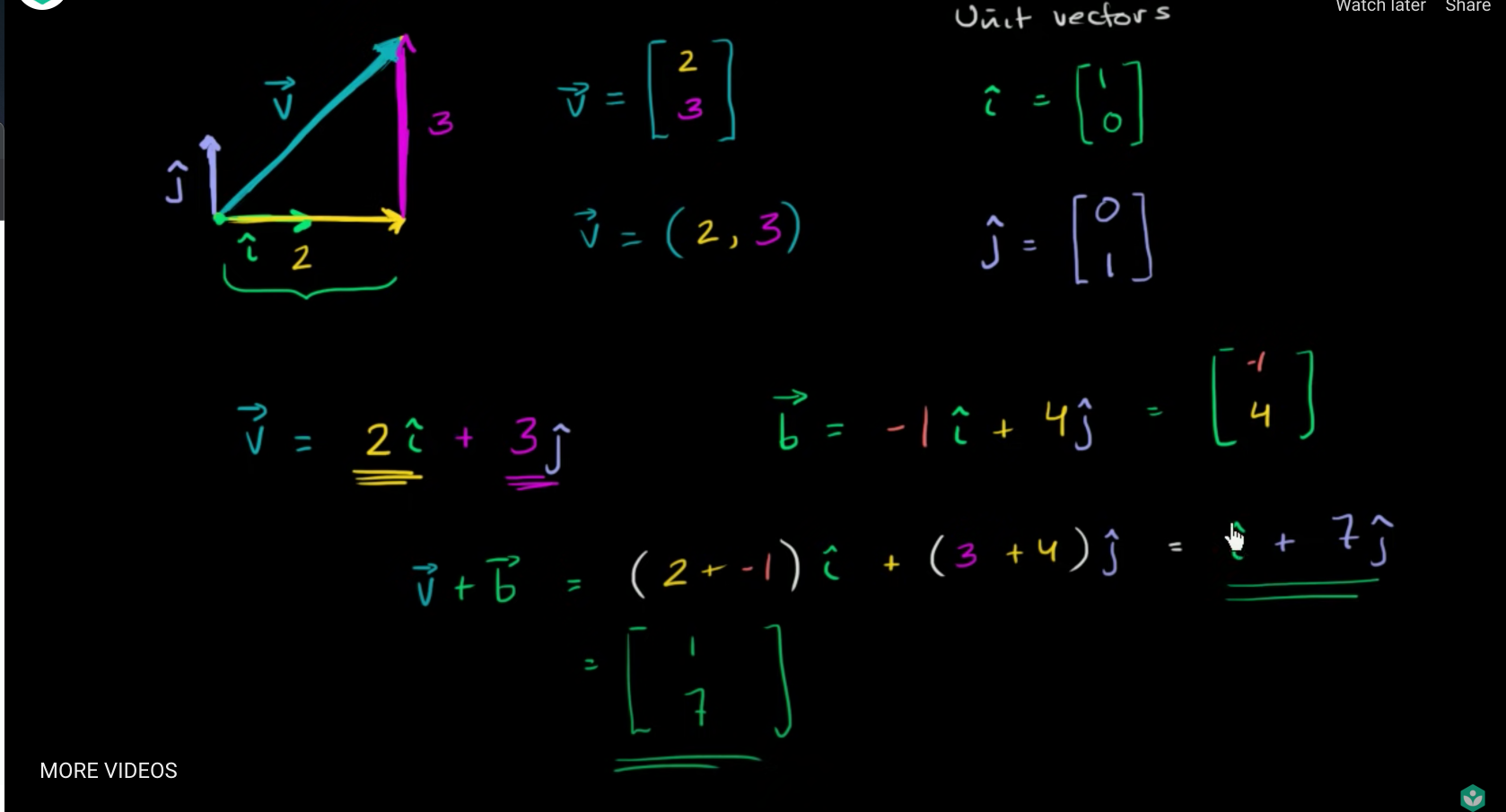
- 가로 :
i^, 세로 :j^, 깊이 :k^ - 특정 벡터를 단위벡터의 합으로 표현이 가능
- 단위벡터의 합은 일반 벡터로 표현가능
- 구하는 공식
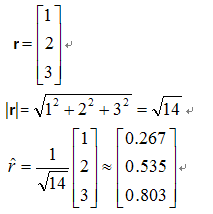
직선의 매개변수 표현
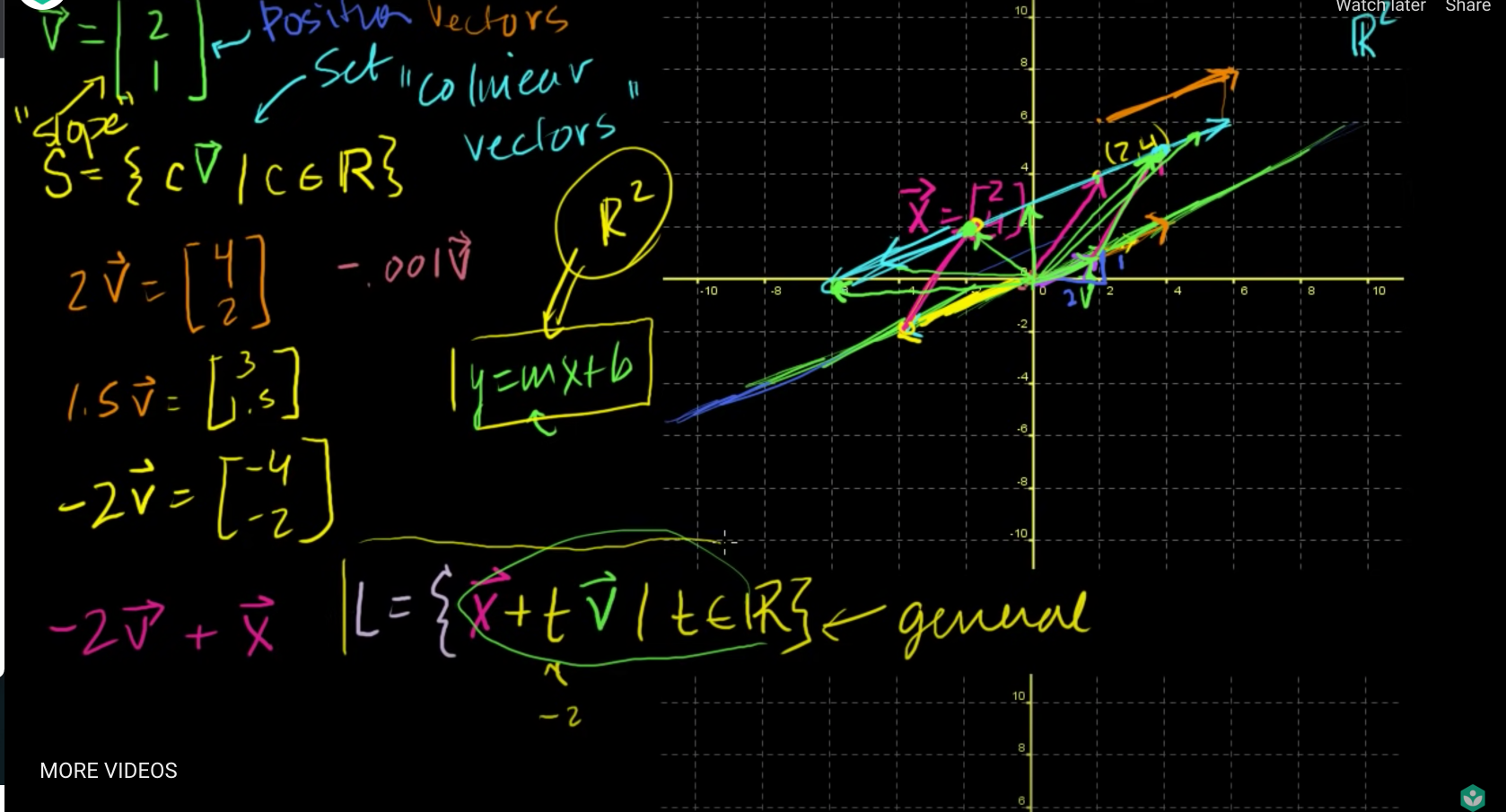
- s = {c * v^→ | c ⍷ R}
- c - R ^ 1
L = {x^→ + t * v^→ | t ⍷ R}- x^→ : 시작점 표현 가능
- 원래는 y= ax + b와 같이 표현이 되는데 굳이 위와 같이 표현을 하는 이유는 차원이 100차원 가까이되면 표현이 힘들기 때문에 일반적인 표현 사용
.jpeg)