[ 나의 풀이 ]
#include <string>
#include <vector>
#include <map>
#include <iostream>
#include <algorithm>
using namespace std;
int solution(vector<vector<string>> relation) {
int answer = 0;
int m = relation.size();
int n = relation[0].size();
vector<int> candidate;
vector<vector<int>> all((1<<n));
for(int i=1;i<(1<<n);i++){
for(int j=0;j<n;j++){
int t = 1 & (i >> j);
if(t == 1) all[i].push_back(j);
}
}
for(int i=0;i<all.size();i++){
map<string,int> temp;
int flag=0;
vector<int> del;
for(int k=0;k<m;k++){
string str = "";
for(int j=0;j<all[i].size();j++)
{
int idx = all[i][j];
auto it = find(del.begin(), del.end(), idx);
if(it == del.end()) del.push_back(idx);
str += " " + relation[k][idx];
}
str.erase(0,1);
if(temp[str]) {
flag = 1;
break;
}else temp[str]++;
}
if(flag == 0) {
bool check = true;
for(int q=0;q<candidate.size();q++){
if((candidate[q] & i) == candidate[q]){
check=false;
break;
}
}
if(check) candidate.push_back(i);
}
}
return candidate.size();
}
- 모든 경우의수를 처리하는 방법을 못찾아서 힌트를 참조함
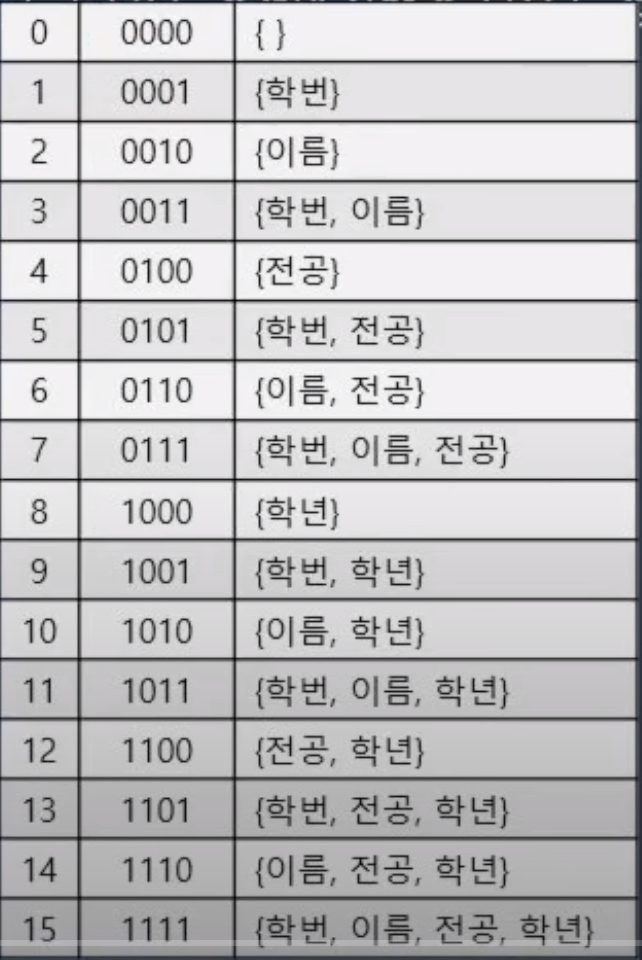
- key point!
1) 모든 cloumn의 경우의수를 구해서 정해놓아야 한다
: 1 << Col의 수 로 모든 경우의 수의 개수가 나온다
ex) column이 4개일 때 1<<4 = 10000 이므로,
0000 ~ 1111까지!!
2) 현재 후보키로 선정된 column이 모두 포함된 다른 경우의수를 배제해야함
--> 최소성을 만족시키기 위해서!
3) 유일성을 만족시키기 위해 Map을 사용함
[ 최적 풀이 ]
#include <bits/stdc++.h>
using namespace std;
bool possi(vector<int> &vec,int now){
for(int i=0;i<vec.size();i++)
if((vec[i]&now)==vec[i])return false;
return true;
}
int solution(vector<vector<string>> relation) {
int n=relation.size();
int m=relation[0].size();
vector<int> ans;
for(int i=1;i<(1<<m);i++){
set<string> s;
for(int j=0;j<n;j++){
string now="";
for(int k=0;k<m;k++){
if(i&(1<<k))now+=relation[j][k];
}
s.insert(now);
}
if(s.size()==n && possi(ans,i)) ans.push_back(i);
}
return ans.size();
}
- 유일성 검사를 따로 해주지 않음
--> 값이 증가하며 비트가 순서대로 커지기 때문에 해당 column이 포함된 경우가 차례로 등장해서 안해줘도 되는것으로 보임
- 최소성 검사
(후보키)A & (현재 검사하는 후보키)B = (후보키)A
: 앞서 나온 후보키 A의 비트와 현재 검사하는 키 B를 &연산 했을 때 A가 나오면
적어도 A의 비트는 포함되어 있는 것이기 때문에 후보키가 될수 없음을 알 수 있음!