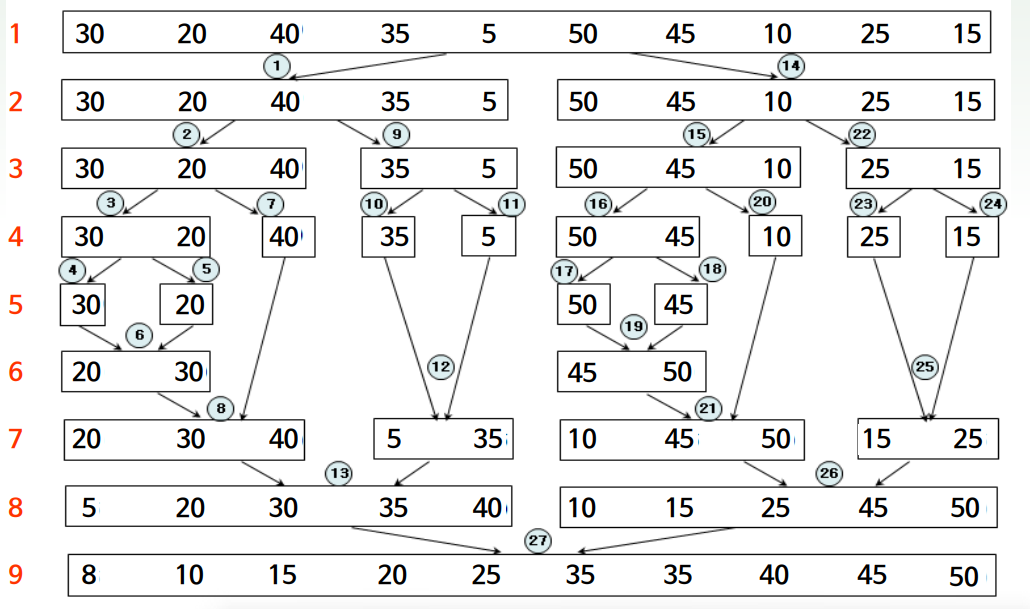
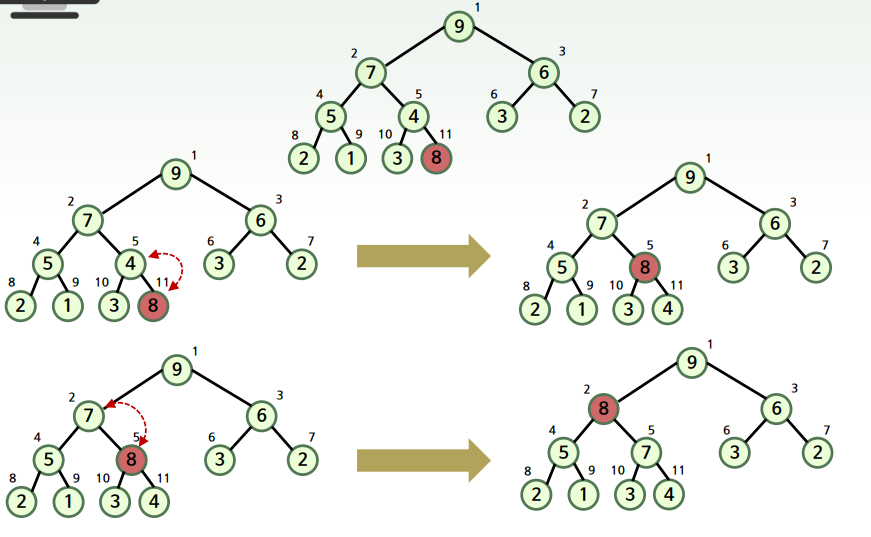
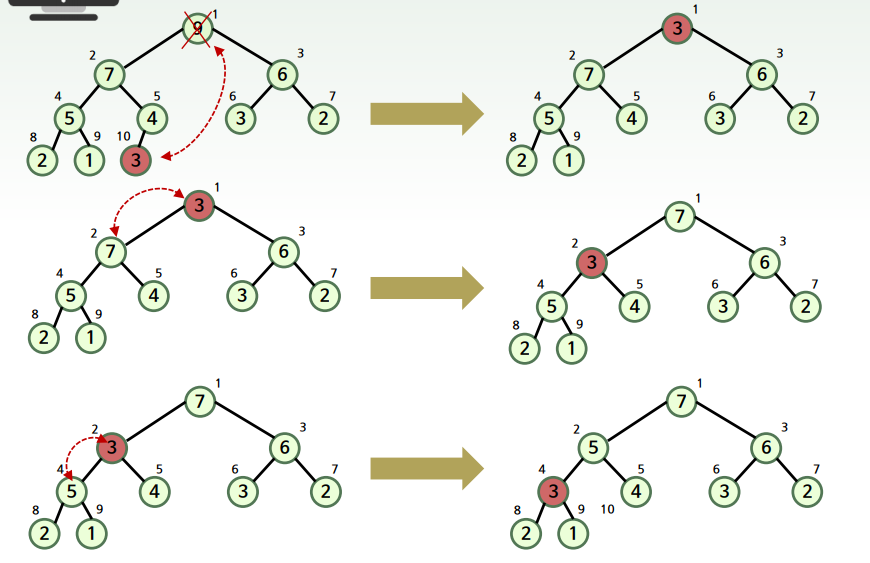
합병 정렬

• 원소의 개수가 1개가 될때까지 분할한다
• 이후 병합을 시작하는데 병합을 분할의 역순이다.

• 합병 정렬 과정중 분할 과정을 나타낸 것이다.
• 재귀함수로 구성되어있고, 원소의 개수가 1이되는 지점 즉, if문이 거짓이 되는 지점에서 종료된다.

• 합병 정렬 과정중 합병 과정을 나타낸 것이다.
• Buffer라는 가상의 공간을 생성해서 정렬된 원소들을 계속해서 Buffer에 집어넣고 마지막에는 다시 Buffer의 결과값을 원래 배열에 삽입한다.

• 제자리성 : 입력크기에 비례하는 B행렬(=Buffer) 필요, 제자리 정렬 X
• 안정성 : 순차적 이동 , 안정
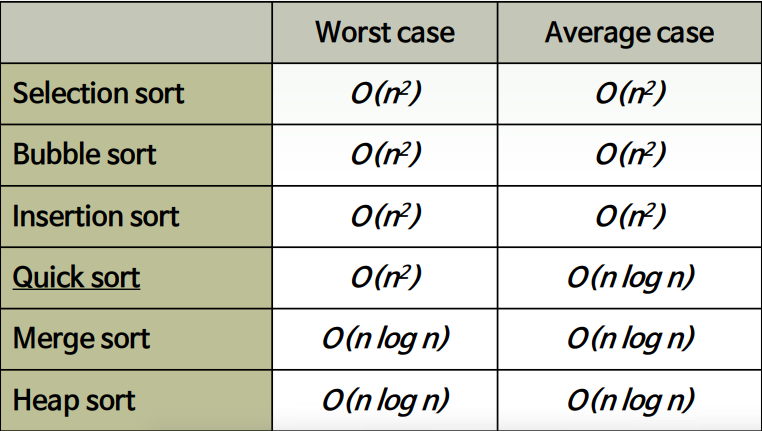
• 최선시간 복잡도 : min(m,n)
  • EX. 2 3 4 0 1 7 8 9 5 6
• 최악시간 복잡도 : m+n-1 , O(nlogn)
  • 단, m = Mid-Left+1, n = Right-(Mid+1)+1
  • EX. 0 8 4 2 6 1 9 5 3 7

힙 정렬

힙이란?

• 노드들이 저장하고 있는 키들이 다음 성질을 만족하는 완전이진트리 형태의 자료구조
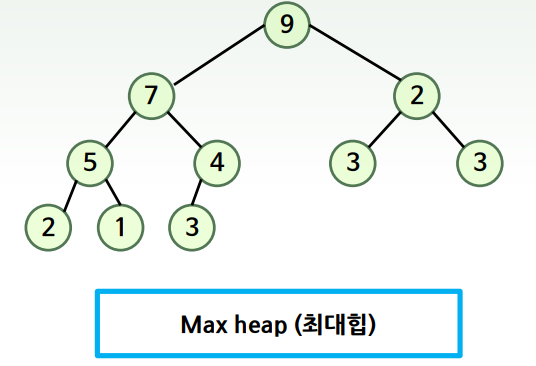
• 최대 힙(max heap)
  
  • 부모 노드의 키 값이 자식 노드의 키 값보다 크거나 같은 완전 이진 트리
  • key(부모 노드) ≥ key(자식 노드)
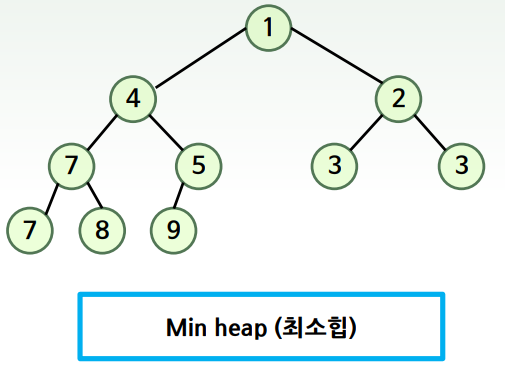
• 최소 힙(min heap)
  
  • 부모 노드의 키값이 자식 노드의 키 값보다
    작거나 같은 완전이진트리
  • key(부모 노드) ≤ key(자식 노드)
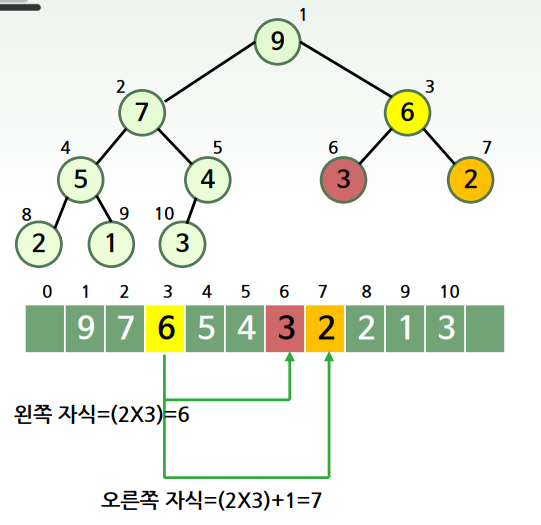
• 배열을 이용하여 구현 가능
  • 완전이진트리이므로 각 노드에 번호(인덱스) 부여 가능

• L자식 인덱스 = (부모 인덱스)*2
• R자식 인덱스 = (부모 인덱스)*2 + 1
• 부모 인덱스 = (자식 인덱스)/2

Upheap 연산

• 삽입할 노드를 마지막 위치에 삽입
• 삽입된 노드로부터 루트까지의 경로에 있는 노드들의 키 값을 비교, 교환함으로써 Heap 성질 복원
• 키 값이 부모 노드보다 작거나 같으면 종료
• 시간 복잡도: O(logn)
  

Downheap 연산

• 루트 노드 복사 후 삭제
• 마지막 노드를 루트로 이동
• 루트에서 단말 노드까지의 경로에 있는 노드들의 키 값을 비교, 교환함으로써 Heap 성질 복원
• 키 값이 자식 노드보다 크거나 같으면 종료
• 시간 복잡도: O(logn)
  

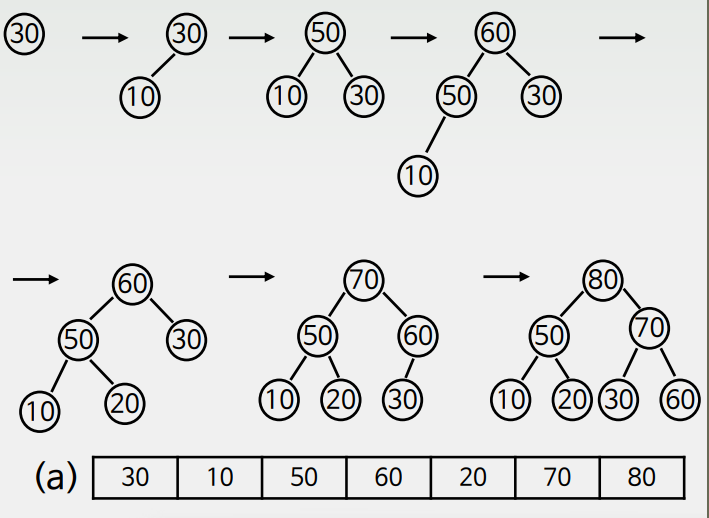
힙 정렬 설계

• 먼저 정렬할 n개 레코드를 최대 Heap에 삽입(Upheap)
• 한 번에 하나씩 레코드를 Heap에서 삭제하여 저장 (Downheap)
• 힙 생성시 레코드 추가할 때마다 Heap 조정 필요
  = 한번 정렬할때마다 Max Heap, Min Heap 성질이 유지되는지 살펴야함

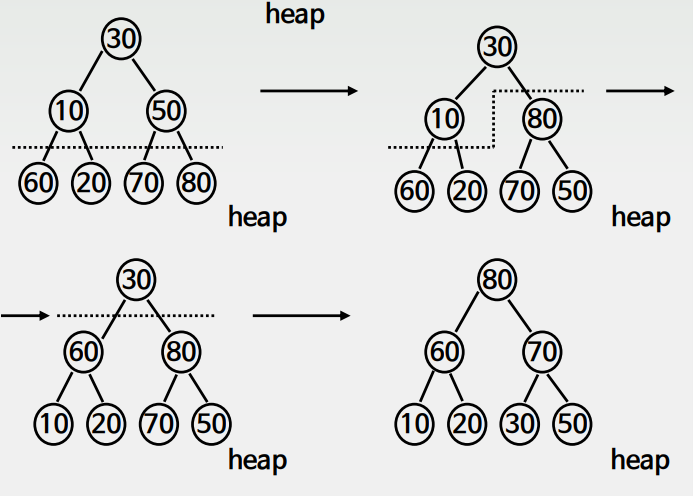
개선된 힙생성 연산 Make Heap 설계

• 말단 노드부터 시작해서 역으로 루트노드까지 생성하는 과정
• 말단 노드가 이미 구성되어있다는 가정하에 데이터가 추가됬을때 해당 부분에서만 Max Heap 성질을 유지하기 위해 Heap 조정을 한다.
• 미리 N개 레코드가 모두 주어진 경우에만 가능
  = 순차적으로 들어오는 데이터에는 사용 불가

• 제자리성 : 제자리 정렬
  • i, Parent, LeftSon, RightSon, Son, RootValue 등 상수크기 메모리 사용
• 안정성 : 불안정
• 최악시간복잡도 = O(nlogn)
  • EX) 이미 정렬된 입력 : 10 20 30 50 60 70 80

정렬 알고리즘 시간복잡도 비교