분할정복

• 주어진 문제의 입력을 분할해 문제를 해결하는 기법

예시 : 아주 많은 동전 더미 속에 1개의 가짜 동전이 섞여 있다. 이 가짜 동전은 매우 정교하게 만들어져 누구도 눈으로 가짜인지를 식별할 수 는 없지만, 무게가 정상적인 동전보다 약간 가볍다. 1개의 양팔 저울만을 사용해 이 가짜 동전을 최소한의 저울질로 찾아낼 수 있는 방법은 무엇인가?

Solution1 : 매 시행마다 양팔 저울에 동전 한개씩 올려서 비교한다.

• 매우 비효율적이다

Solution2 : 매 시행마다 양팔 저울에 두개의 그룹으로 나눈 동전 더미를 올려서 비교한다.

• 동전 더미가 2의 배수라면 매 시행마다 두 그룹으로 나눌 수 있지만, 2의 배수가 아니라면 어느 순간에 홀수개가 되기 때문에 구현이 어렵다.

Solution3 : 두개의 그룹으로 나누는 것이 아닌, 저울에 올라가지 않는 동전더미 그룹을 하나 더 만들어 총 세개의 그룹으로 나눈다.

• 매 시행마다 2/3의 동전 더미를 배제시킬 수 있다.

< N개 수의 합 구하기 >

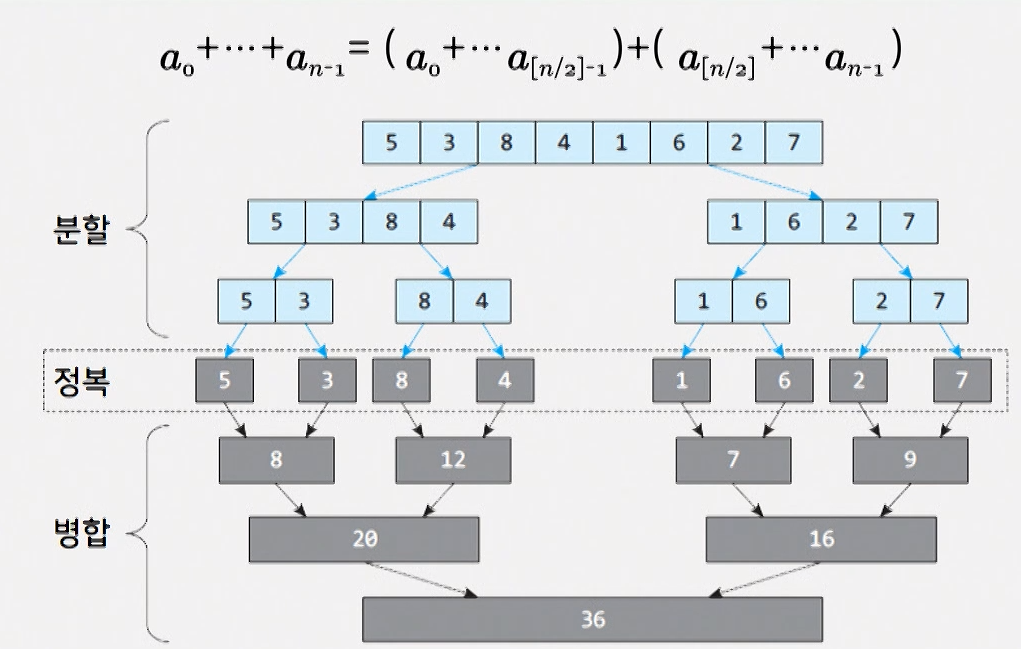
• N개 수의 합을 그냥 더해도 N-1번의 연산횟수가 필요하다
• 분할정복을 이용하여 구해도 N-1번의 연산횟수가 필요하다
• 분할정복을 이용한다해서 반드시 유리한 것은 아니다.

< 거듭제곱 프로그래밍 >

• 숫자 x의 n제곱값을 구하는 문제 : x^n
• 반복적인 방법 : 그냥 x를 계속해서 곱한다
  -> n번의 연산횟수가 필요하다.
• 순환적인 방법 (분할정복)

  double power(double x, int n)
  {
      if (n==0) return 1;
      else if ((n%2)==0) # 짝수일 경우
          return power(x*x,n/2);
      else return x*power(x*x,(n-1)/2); # 홀수일 경우, x^25=x^12*x^12*x
  }

• x^100을 구하기 위해 반복적인 방법을 사용하면 총 100번의 연산이 필요하다.
• x^100=x^50 * x^50을 이용하여 작은 문제로 분할하는 분할정복을 이용한다.
• 분할정복을 이용하게 되면 x^100을 구하기 위해 총 8번의 연산이 필요하기 때문에 훨씬 효율적이다.

---

DP (Dynamic Programming)

• 복잡한 문제를 풀기 위해서, 간단한 여러 개의 하위 문제로 나누어 푼 뒤, 그것을 결합하여 최종적인 목적에 도달하는 방법
• 분할정복 VS DP

  • 하위 문제 간 겹침이 발생하지 않을 경우 분할정복이 효율적
  • 하위 문제 간 겹침이 발생하는 경우 DP가 효율적
  • DP와 분할정복의 가장 큰 공통점은 가장 간단한 문제로 분할 한다는 점이지만, 가장 큰 차이점은 DP는 가장 작은 문제를 풀고 memoization을 통해 결과를 기록하고 기록한 결과를 이용하여 다음 큰 문제를 푼다는 점이다. 분할정복은 가장 간단한 문제를 풀고 재귀를 이용하여 다음 큰 문제를 푼다.

• 분할정복에 비해 DP는 시간복잡도가 매우 빠르다. 따라서 매우 빠른 시간 복잡도를 요구한다면 보통 DP를 이용하여 풀어야한다. 하지만 시간복잡도가 넉넉하다면 굳이 DP가 아닌 분할정복을 이용해서 풀어도 된다.

피보나치 수열 (분할정복)

int fib(int n){
    if (n<=0) return 0;
    else if (n==1) return 1;
    else return fib(n-1) + fib(n-2); }

• 이미 계산했던 것을 다시 계산하는 비효율성이 있다.

피보나치 수열 (DP, Bottom-up)

int fib(int n){
    int map[n+1]; map[0]=0; map[1]=1;
    if (n<=0) return map[0];
    else if (n==1) return map[1];
    else{
        for (i=2; i<=n; i++)
            map[n]= map[n-1]+map[n-2] # "기억하기"
        return map[n]; }}

• 겹치는 동일 계산을 함수 내 "기억하기(Memoization)" 과정을 통해 회피
• Bottom-up 방식은 작은 문제부터 memoization을 통해 기록하면서 큰 문제를 푸는 방식
• 보통 Bottom-up 방식은 for문을 이용한다.

피보나치 수열 (DP, Top-Down)

int map[n+1]; map[0]=0; map[1]=1;
int fib(int) {
    if( map(n) is ready) return map[n];
    else{
        map[n]=fib[n-1] + fib[n-2];
        return map[n]; }}

• 겹치는 동일 계산을 함수 내 "기억하기(Memoization)" 과정을 통해 회피
• Top-Down 방식은 큰 문제부터 작은 문제로 내려가면서 기록되어 있는지 체크하고 기록이 안되어 있으면 재귀를 통해 그 다음 큰 문제를 호출한다.
• 보통 Top-Down 방식은 재귀를 이용한다.

📒 보통은 Top-Down 방식이든 Bottom-Up 방식을 사용하든 문제를 푸는데 지장이 없지만 상황에 따라 더 효율적인 방식이 존재한다.

< 동전 거스름돈 문제 >

• 예시로, 1원부터 180원까지 최소 동전의 수가 Memoization되어 있을때 680에서 500원 동전을 사용하게 되면 1개 추가 + C[j-500]
  즉, 1 + C[180]이 680의 최소 동전의 수가 된다.
• DP를 풀기위해서는 점화식 또는 수열의 귀납적 정의를 활용해야 한다.
• 점화식을 도출하기 위해서는 내가 선택할 수 있는 선택지를 모두 나열해보는 것도 좋다 (EX. 500원, 100원, 50원, 10원, 1원)

📒 나는 DP문제의 경우 차트(표)를 하나 그려서 나올 수 있는 모든 경우의 수를 적어보고, 규칙을 찾아내어 점화식을 생성한다.

• if문은 사용가능 동전과 업데이트 될 경우를 나타낸 것이다.
• if문 아래에는 업데이트를 수행한다.
• 0원은 0, 1원은 1, 2원은 2, ... 9원은 9가 된 상태에서 10원이 들어오면 10원은 1원과 10원이 둘다 사용가능하다. 이때 10원에서 1을 뺀 9의 값을 가져오면 9 + 1이 된다. 하지만 10을 빼게되면 0이 되고 0은 0이기 때문에 0 + 1이 된다. 따라서 10은 최소값인 1로 Memoization이 된다.