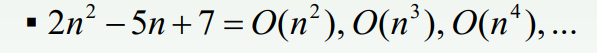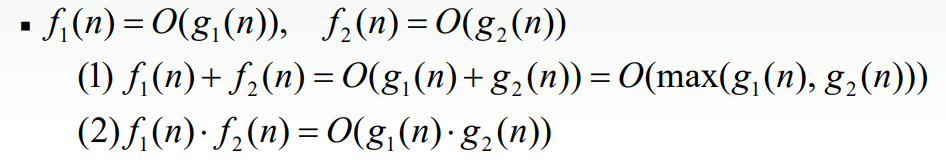빅오 표기법

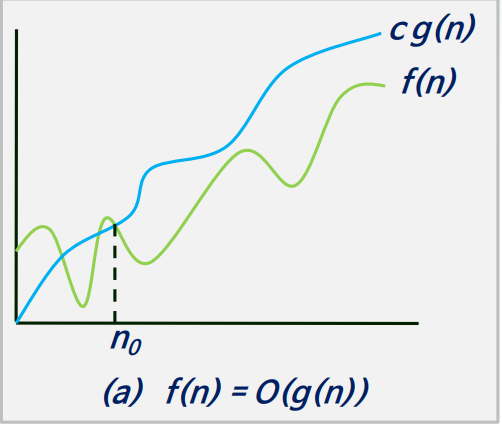
• 연산 횟수를 대략적(점근적)으로 표기한 것으로 함수의 상한을 의미함
• 두 개의 함수 f(n)과 g(n)이 주어졌을 때, 모든 n≥n0에 대하여
  |f(n)| ≤ c|g(n)|을 만족하는 2개의 상수 c와 n0가 존재하면
  f(n) = O(g(n)) 이다.
• ex) n≥2 이면 n2+n+1<2n2 이므로 n2+n+1 = O(n2)
  
  -> n이 1000인경우 n2+n+1은 1001001이고 n2은 1000000이다.
  n2으로 표현해도 전체의 99%를 표현할 수 있으므로 최고차항이 전체함수에 지배적이라고 볼 수 있다.

• O(n2)을 만족한다면 거기에 상수배를 하거나 최고차항의 계수가 더 큰 것은 항상 만족한다

• 위의 함수처럼 두개 함수가 존재한다면, 덧셈과 곱셉 법칙을 만족한다

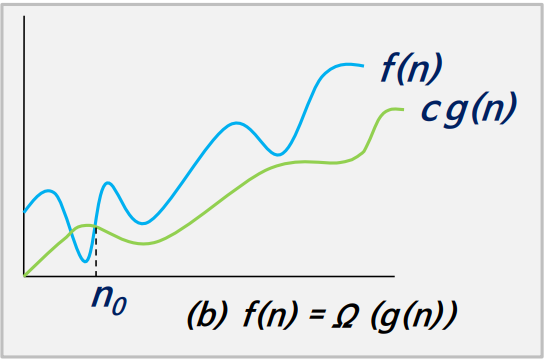
빅오메가 표기법

빅오 표기법 이외의 표기법

• 모든 n≥n0에 대하여 |f(n)| ≥ c|g(n)|을 만족하는 2개의 상수 c와 n0가 존재하면 f(n)=Ω(g(n))이다.
• 빅오메가는 함수의 하한을 표시한다.
• ex) n ≥ 0 이면 2n+1 > n 이므로 2n+1 = Ω(n)
  

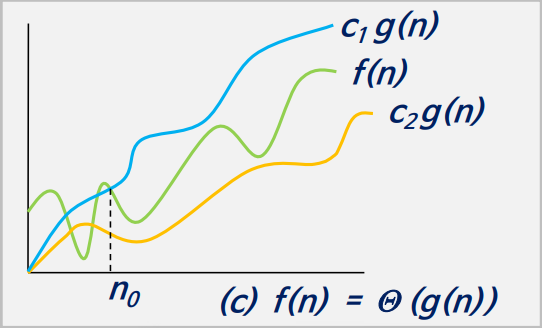
빅세타 표기법

빅오 표기법과 빅오메가 표기법을 융합합 방법이다

• 모든 n≥n0에 대하여 c1|g(n)| ≤ |f(n)| ≤ c2|g(n)|을 만족하는
  3개의 상수 c1, c2와 n0가 존재하면 f(n)=θ(g(n))이다.
• 빅세타는 함수의 하한인 동시에 상한을 표시한다.
• f(n)=O(g(n))이면서 f(n)= Ω(g(n))이면 f(n)= θ(g(n))이다.
• ex) n ≥ 1이면 n ≤ 2n+1 ≤ 3n이므로 2n+1 = θ(n)
  

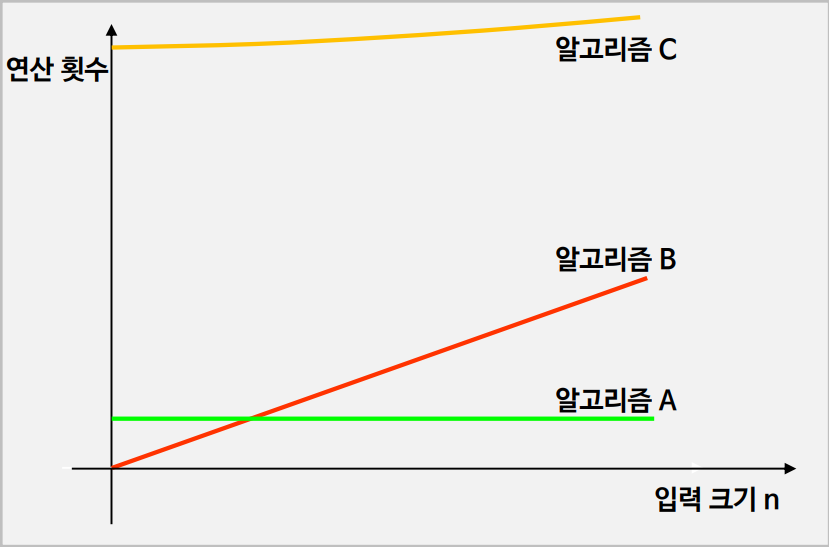
알고리즘 성능 비교

• 연산횟수가 적을수록 더 좋은 알고리즘이다
• 알고리즘 B와 A가 만나는 지점을 n0라 했을 때 입력크기가 n0보다 작다면 B가 A보다 좋은 알고리즘, n0보다 크다면 A가 B보다 좋은 알고리즘이다.
• 이처럼 입력크기의 구간을 나누어서 알고리즘의 성능을 비교해야 한다

• 알고리즘의 수행시간은 입력 자료 집합에 따라 다를 수도 있다.
• 빅오 표기법의 실제 활용
  • 최선의 경우 : 의미 없는 경우가 많다.
  • 평균적인 경우 : 계산하기가 상당히 어렵다
  • 최악의 경우 : 가장 널리 사용된다, 계산하기 쉽고 응용에 따라 중요한 의미를 가질 수도 있다

정렬이란

• 레코드(정령 대상 원소) 들을 순서대로 재배치하는 일
• 정렬시간 = 레코드 접근시간 + 레코드 비교 / 재배치 시간
  • 레코드 접근시간은 매우 짧다

내부 정렬

• Input : 레코드의 순서
• Output : 재정렬된 레코드
• 비교-기반 정렬방법과 분포-기반 정렬 방법이 있다

비교-기반 정렬방법

• 선택정렬, 버블정렬, 삽입정렬, 쉘정렬, 퀵정렬, 합병정렬, 힙정렬

분포-기반 정렬방법

• 계수정렬, 기수정렬, 버킷정렬

수행능력 측정

• 시간 복잡도
  • 비교-기반 정렬 : Key의 비교 횟수
  • 분포-기반 정렬 : 레코드의 움직임 횟수
  • 외부 정렬 : 외부 레코드의 접근 횟수
• 공간 복잡도
  • 제자리성을 만족하는지 안하는지가 성능 측정 척도이다
• 안정성
  • 동일한 키 값을 가진 레코드들이 정렬 이후에도 동일한 키값을 가지는지 판단

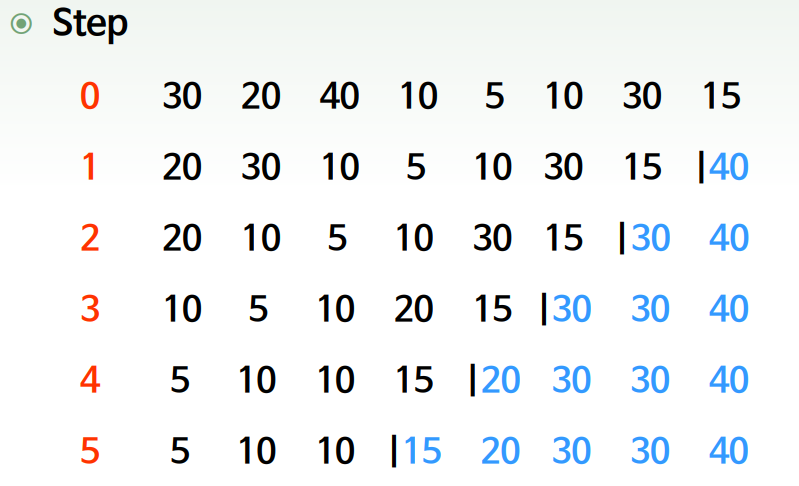
선택 정렬

• 처음 30을 기준으로 30 다음 인덱스의 값들 중에서 가장 작은 값을 찾아낸다.
• 가장 작은 값인 5와 처음 기준인 30의 자리를 바꾼다
• 이 과정을 반복한다

• i번째 단계에서 항상 n-i회 비교수행 > 복잡도는 입력 자료 순서와 무관
• 평균시간 복잡도 = O(n2)
• 최악시간 복잡도 = O(n2)
• 제자리성 : 제자리 정렬
  • i, j, MinIndex 등 상수 크기 메모리
• 안정성 : 불안정한 정렬

버블 정렬

• 버블 정렬은 매시행마다 처음값부터 시작해 인접한 값하고만 비교를 하여 오른쪽에 있는 값이 작다면 자리를 바꾸는 방식이다
• 매시행마다 가장 큰 값을 가장 우측에 배치한다.
• 다음 시행에서는 가장 우측에 배치한 값을 제외하고 반복한다
• 이러한 과정을 반복한다.

하지만 위의 버블정렬은 4번째 시행에서 이미 정렬되었음에도 불구하고 5번째에서 결과에 영향이 없는 , 즉 의미가 없는 시행을 한다

• Sorted를 판별하기 위한 Flag를 설정함으로서 불필요한 정렬횟수의 낭비를 방지한다.
• 제자리성 : 제자리 정렬
  • i , Sorted 등 상수 크기 메모리
• 안정성 : 안정된 정렬, 인접한 레코드끼리만 자리바꿈
• 평균시간 복잡도 : O(n2)
• 최악시간 복잡도 : O(n2)
  • 역순으로 이미 정렬된 레코드