자료구조와 시간복잡도

자료구조

자료구조 → 메모리 효율적 사용, 빠르고 안정적인 데이터 처리
완벽한 자료구조는 없다! 특정 상황에서 유용한 자료구조와 덜 유용한 자료구조가 존재할 뿐이다. 우리는 상황에 맞게 적절한 자료구조를 선택하면 된다.

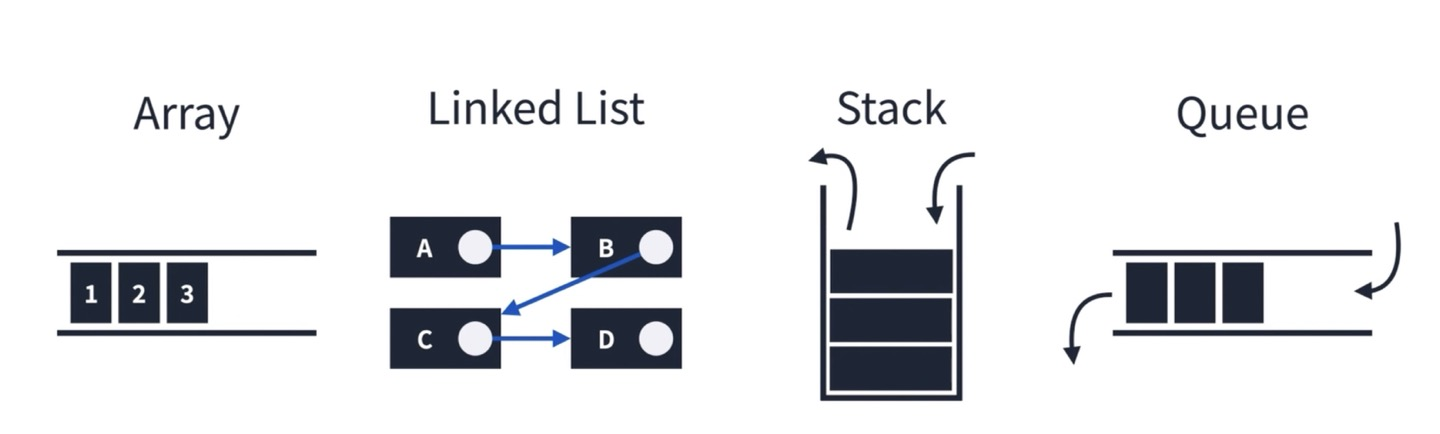
1. 선형 구조

한 원소 뒤에 하나의 원소 만이 존재하는 형태, 자료들이 선형으로 나열되어 있는 구조
ex) 배열, 연결 리스트, 스택, 큐

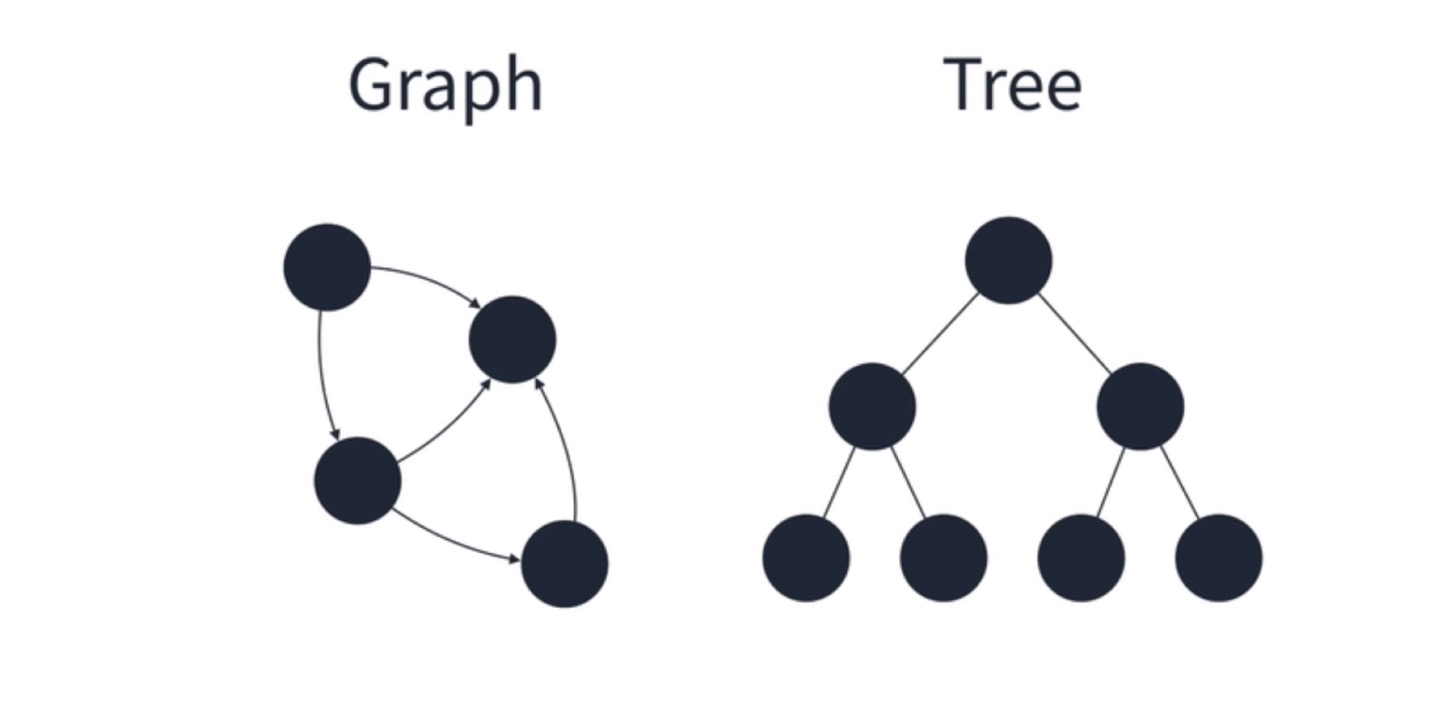
2. 비선형 구조

원소 간 다대다 관계를 가지는 구조, 계층적 구조 or 망형 구조를 표현하기 적절하다.
ex) 그래프, 트리

---

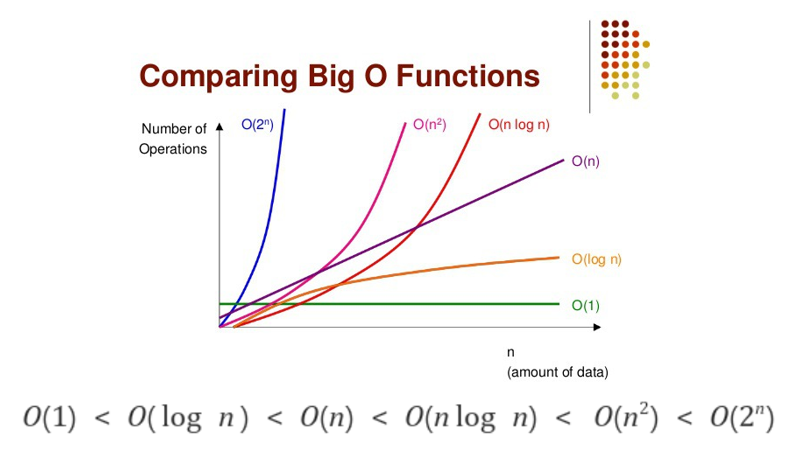
BIG-O Notation (빅오 표기법)

알고리즘의 효율성은 데이터의 개수(n)가 주어졌을 때 덧셈, 뺄셈, 곱셈 등의 기본 연산 횟수를 의미한다. 빅오 표기법은 알고리즘의 효율성을 나타낼 때 쓰이는 함수의 증감 추세를 비교하는 표기법이다.
→ 알고리즘의 시간 복잡도 + 알고리즘의 공간(메모리) 복잡도

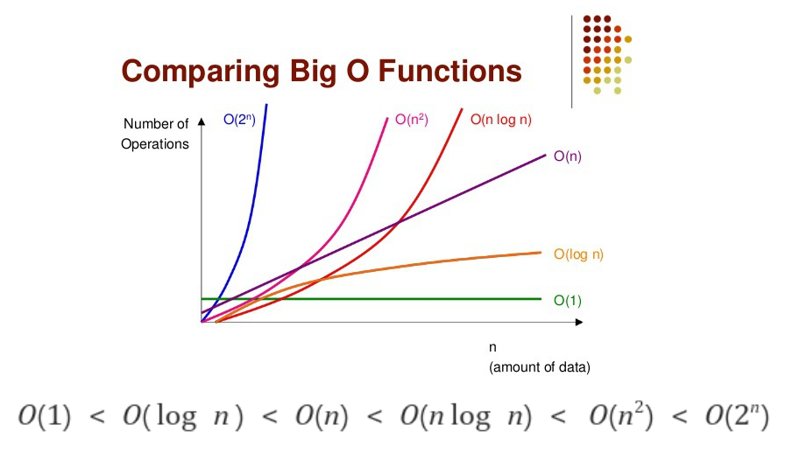
(fsater) 상수함수 < 로그함수 < 선형함수 < 다항함수 < 지수함수 (slower)

빅오 표기법의 수학적 정의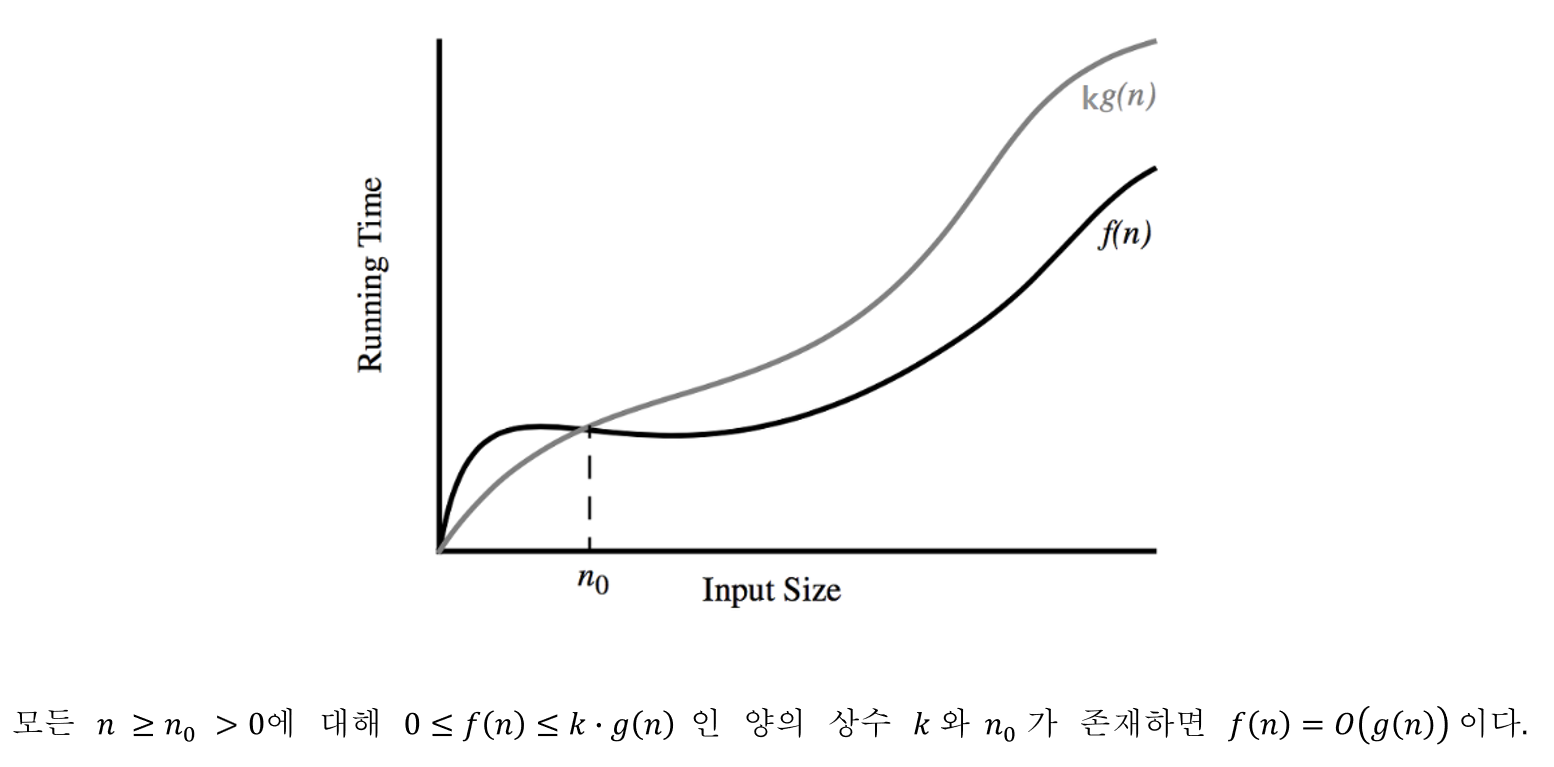

example
어떤 알고리즘의 시간 효율성을 의미하는 f(n) = n2 + 2n + 3 / g(n) = n2
n0보다 충분히 큰 n을 넣었을 때, f(n)의 running time이 최악인 경우에도 점근 상한선 K•g(n)을 넘을 수 없다.
→ f(n) = O(g(n)) = O(n2)

빅오 표기법의 특징

데이터 입력값(n)이 충분히 크다고 가정하고, 알고리즘의 효율성은 데이터 입력값(n)의 크기에 영향을 받기 때문에 상수항 & 영향력 없는 항은 무시한다.

1. 상수항 무시
   ex) O(2n) → O(n)

2. 영향력 없는 항 무시
   ex) O(n2+2n+1) → O(n2)
   
   
   

빅오 표기법의 예제

/* 자바스크립트 */
for(let i = 0; i < n; i+=1){      // O(n) 선형함수 
}


for(let i = 0; i < n; i*=2){      // O(logn) 로그함수
}


for(let i = 0; i < n; i+=1){      // O(n•logn) 다항함수 
  for(let j = 0; j < n; j*=2){
  }
}


for(let i = 0; i < n; i+=1){      // O(n2) 지수함수 
  for(let j = 0; j < n; j+=1){
  }
}