Gradient Vector는 정의역 상에 정의된 Vector다.

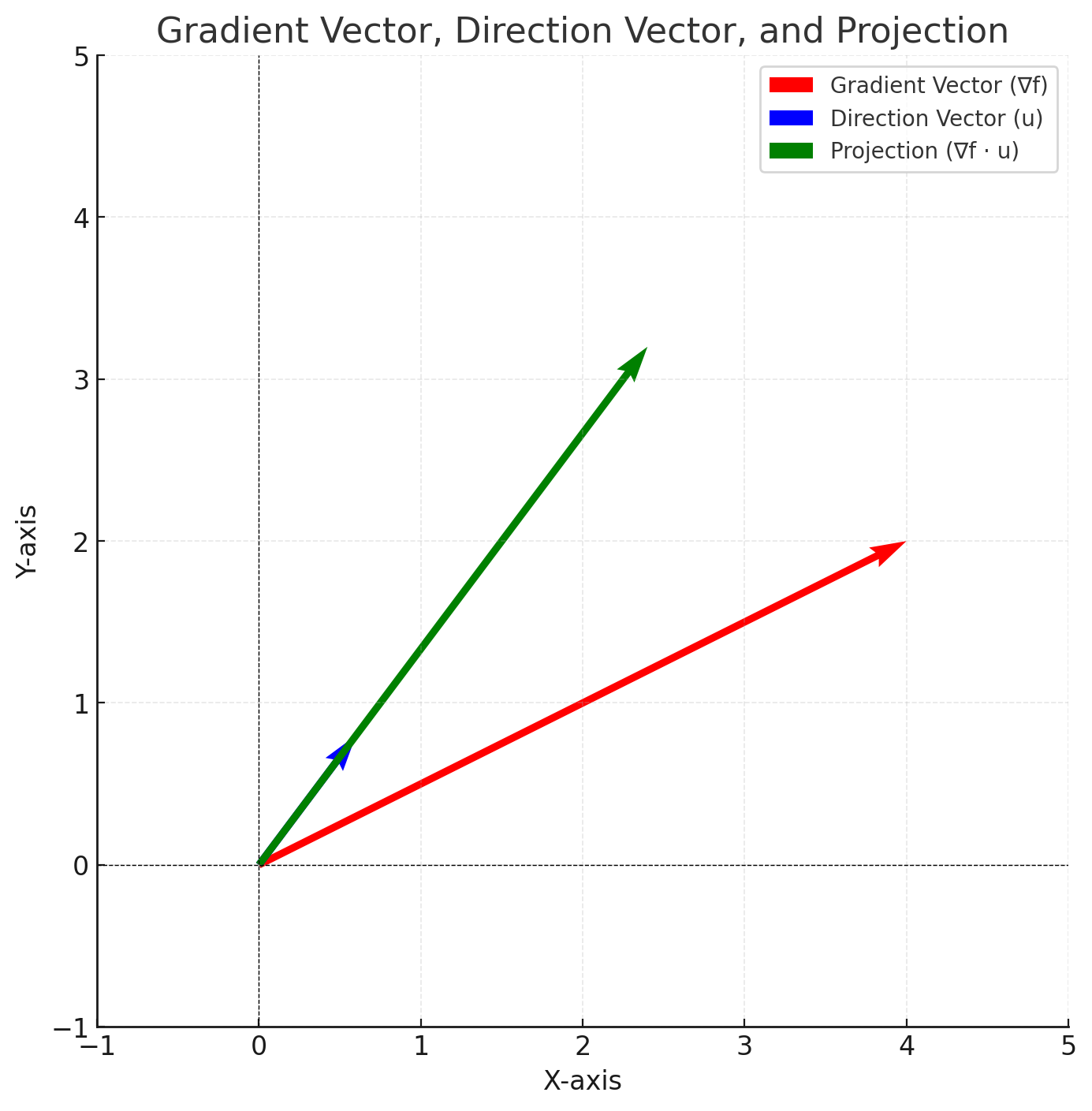
🏷️Gradient Vector

• 특정 방향 $\mathbf{u}$에서 함수 변화율($D_{\mathbf{u}} f$, 방향 도함수)을 계산하려는 이유는, 함수 $f(x, y)$가 $x$-축과 $y$-축 이외의 임의 방향에서 얼마나 빠르게 변하는지를 알고 싶기 때문이다.
  • $x$-방향에서의 함수 변화율: $\frac{\partial f}{\partial x}$
  • $y$-방향에서의 함수 변화율: $\frac{\partial f}{\partial y}$
• To this end, 특정한 방향 $\mathbf{u} = (u_x, u_y)$에 따라 $x$-방향의 함수 변화율과 $y$-방향의 함수 변화율을 적절히 합성해야 한다.
• 이 합성은 $x$-방향의 함수 변화율과 $u_x$를 곱하고, $y$-방향의 함수 변화율과 $u_y$를 곱한 뒤, 이들을 더하는 방식으로 계산된다.
  $D_{\mathbf{u}} f = \frac{\partial f}{\partial x} u_x + \frac{\partial f}{\partial y} u_y$
• 이 식은 곧 내적의 정의와 동일하다.
  $\nabla f \cdot \mathbf{u} = D_{\mathbf{u}} f$
• $x$-축과 $y$-축으로 나누어 생각해보자.
• 방향 벡터 $\mathbf{u}$는 $x$-축으로의 기여($u_x$)와 $y$-축으로의 기여($u_y$)로 나눌 수 있다.
• 각 축 방향에서의 기여도(Contribution)는 해당 축에서의 변화율(편미분)을 곱해서 계산한다.
• i.e. 전체 변화율은 두 축에서의 기여도를 더해서 얻는다.
  $\text{변화율} = \left( \frac{\partial f}{\partial x} \cdot u_x \right) + \left( \frac{\partial f}{\partial y} \cdot u_y \right)$
• 내적은 벡터 $\nabla f = \left( \frac{\partial f}{\partial x}, \frac{\partial f}{\partial y} \right)$를 방향 벡터 $\mathbf{u} = (u_x, u_y)$로 Projection한 Scalar값이다.
• 내적 공간이면 Inner Product를 정의할 수 있고 차원과 관계없이 각도를 정의할 수 있다.
  • Inner product 값이 0이면, Pairwise Orthorgonal하게 된다.
• 다시 정리하면, 방향 벡터 $\mathbf{u}$를 따라 함수$f$가 변하는 속도는 각 축에서의 변화율을 조합하여 계산되며, 이 과정이 내적의 정의와 완벽히 일치한다.
  $D_{\mathbf{u}} f=\nabla f \cdot \mathbf{u} = |\nabla f| |\mathbf{u}| \cos\theta$
  • $|\nabla f|$: 그래디언트 벡터의 크기 (함수의 최대 변화율)
  • $|\mathbf{u}|$: 방향 벡터 $\mathbf{u}$의 크기 (Unit Vector라면 $|\mathbf{u}| = 1$).
  • $\cos\theta$: $\nabla f$와 $\mathbf{u}$ 사이의 각도 $\theta$의 코사인 값
• $D_{\mathbf{u}} f$ ($\mathbf{u}$ 방향에서의 함수$f$의 증가율)가 최대가 되려면, $\mathbf{u}$와 $\nabla f$ 사잇각이 0이되어야 한다.
• 즉, 그래디언트 벡터 $\nabla f$는 함수 증가율이 최대가 되는 방향을 나타낸다.
  • 방향 벡터 $\mathbf{u}$가 $\nabla f$와 같은 방향일 때, 함수 증가율이 최대
  • 방향 벡터 $\mathbf{u}$가 $\nabla f$와 반대 방향일 때, 함수 감소율이 최대