• Time Domain의 신호를 orthogonal basis(complex sinusoid)의 성분으로 뽑아내는 것.
• 모든 신호는 무한개의 cos또는 sin(주기 함수)의 합으로 풀어헤칠 수 있다.
• 결국 핵심은 모든 신호는 많은 주파수를 가진 주기 신호의 합으로 이루어져있다는 사실이다.
• 이는 디지털 신호 역시 아날로그 신호의 일종이라는 것을 알 수 있다.

🏷️CTFT

• $\hat{f}(\omega)$: 주파수 영역에서의 신호 (푸리에 변환된 신호)
• $f(t)$: 시간 영역에서의 신호
• $\omega$: 각속도($rad/s$), $\omega = 2\pi f$
• $j$: 복소수 단위 ($j^2 = -1$)
• 각 basis들과 inner product를 수행하면서, 영향을 주는 성분이 있는지 뽑아내는 것이다.
• 즉, 두 벡터가 orthogonal하다면 적분결과가 0이 될 것이고, 아니면 contribution이 있을 것이다.
• 적분 변환 중 한 형태로 라플라스 변환을 더 일반화 시킨 것이다.
• 지수 함수 $e^{\sigma t}$ ($\sigma > 0$)으로 눌러주면 라플라스 변환이 된다.
• DE (Differential Eqeuation)를 대수방정식으로 변환시켜 줘서 Laplace와 함께 유용한 수학적 도구가 되기도 한다.
• 정의는 다음과 같다.

📌Inverse CTFT

• 푸리에 변환된 함수 $\hat{g}(\omega)$에서 원래의 함수 $g(x)$로 복구하기 위해 푸리에 역변환을 사용한다.
  $g(x) := \frac{1}{\sqrt{2\pi}} \int_{-\infty}^{\infty} \hat{g}(\omega) e^{i \omega x} \, d\omega$
• 역변환과 변환을 연산을 자유롭게 하기 위해 $\frac{1}{\sqrt{2\pi}}$를 곱해준 것이다.

📌Properties of Fourier Transform

1. 푸리에 변환의 선형성

2. 도함수의 푸리에 변환

• 미분 한 번 할때마다 $iw$가 튕겨 나온다.

3. CTFT of Convolution

• 두 함수 $f(x)$와 $g(x)$에 대해 합성곱을 다음과 같이 정의한다.
  $(f * g)(x) := \int_{-\infty}^{\infty} f(\tau) g(x - \tau) \, d\tau$
• 시간 영역에서의 합성곱은 주파수 영역에서의 곱셈으로 변환되며 $\sqrt{2\pi}$가 곱해진다.
  $\mathcal{F}(f * g)(x) = \sqrt{2\pi} \, \mathcal{F}(f)\mathcal{F}(g)$
• LTI 시스템에서 $x(t) * h(t)$ (입력 신호 $x(t)$와 시스템의 impulse response $h(t)$의 컨벌루션)의 출력을 간략하게 구할 수 있다.
• 출력 신호의 CTFT는 $Y(\omega) = X(\omega) \cdot H(\omega)$
• Inverse CTFT $y(t) = \mathcal{F}^{-1}\{X(\omega) \cdot H(\omega)\}$

📌Idea

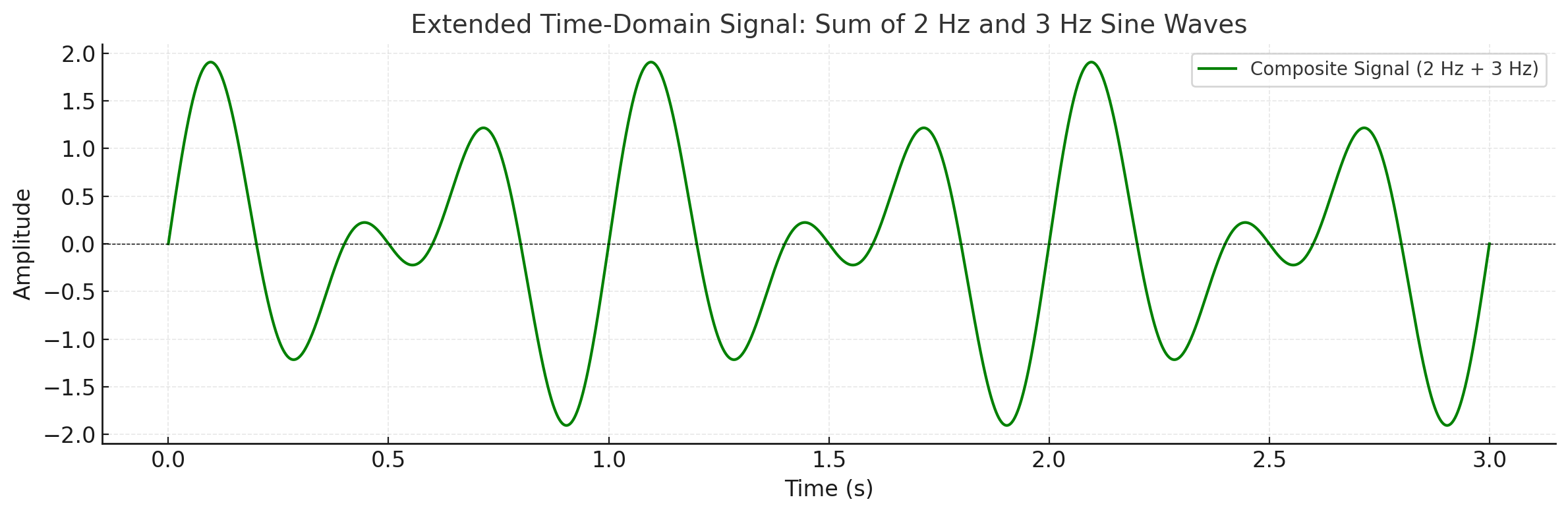
• 위 신호는 $2Hz$와 $3Hz$ 주파수를 가지는 두 사인파의 합성 신호다.
• 이 time domain에서의 신호를 complex plane 상 원에 감다보면 무게 중심이 origin으로부터 크게 벗어나는 순간이 온다.
  
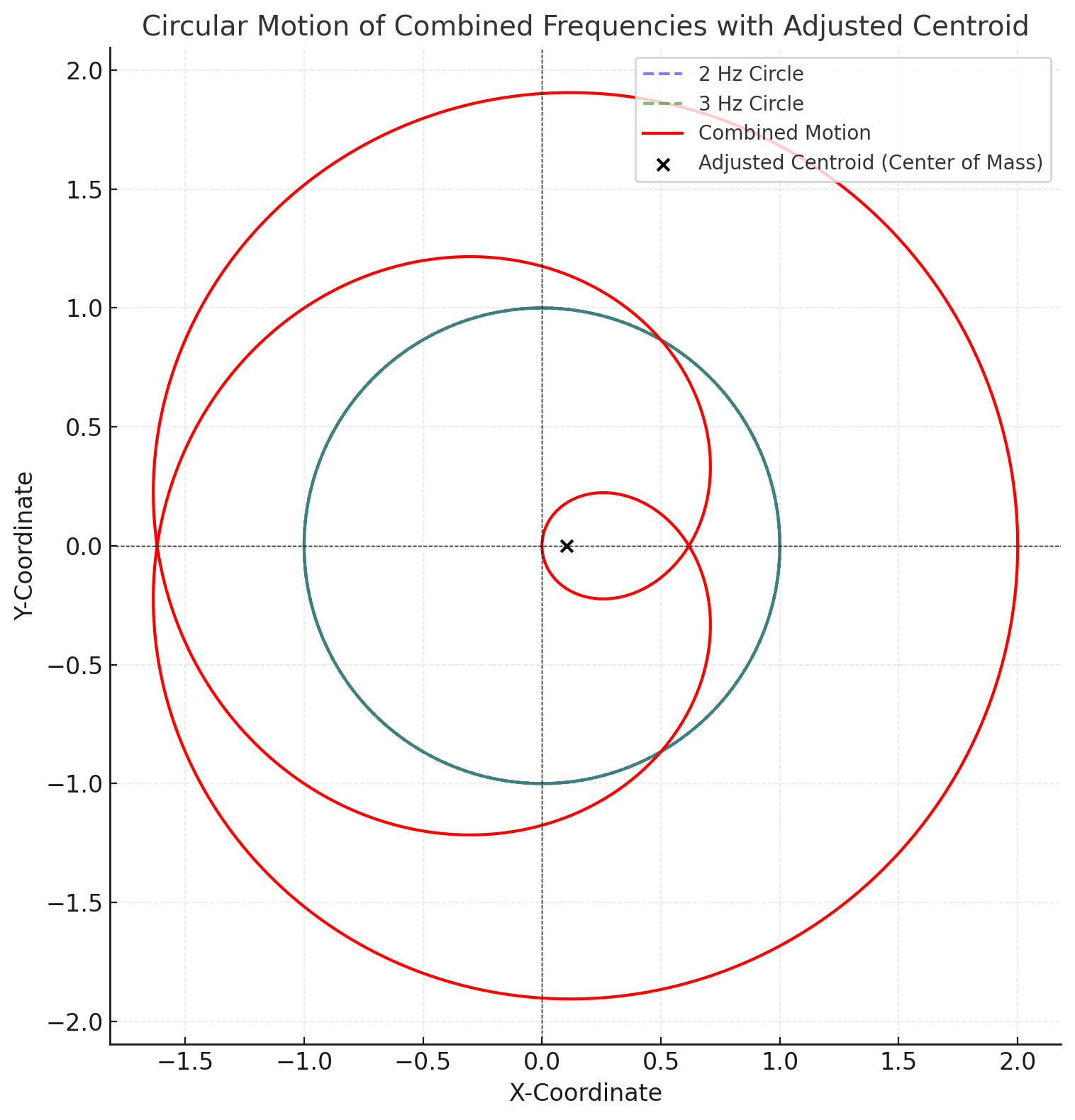
• 이 원리를 통해 어떤 신호들로 합성되어 있는지 분석해낼 수 있다.

📌Expression

• $e^{j2\pi t}$로 복소 평면 상에서 원 위의 점을 나타낼 수 있다.
  • t가 변수
    
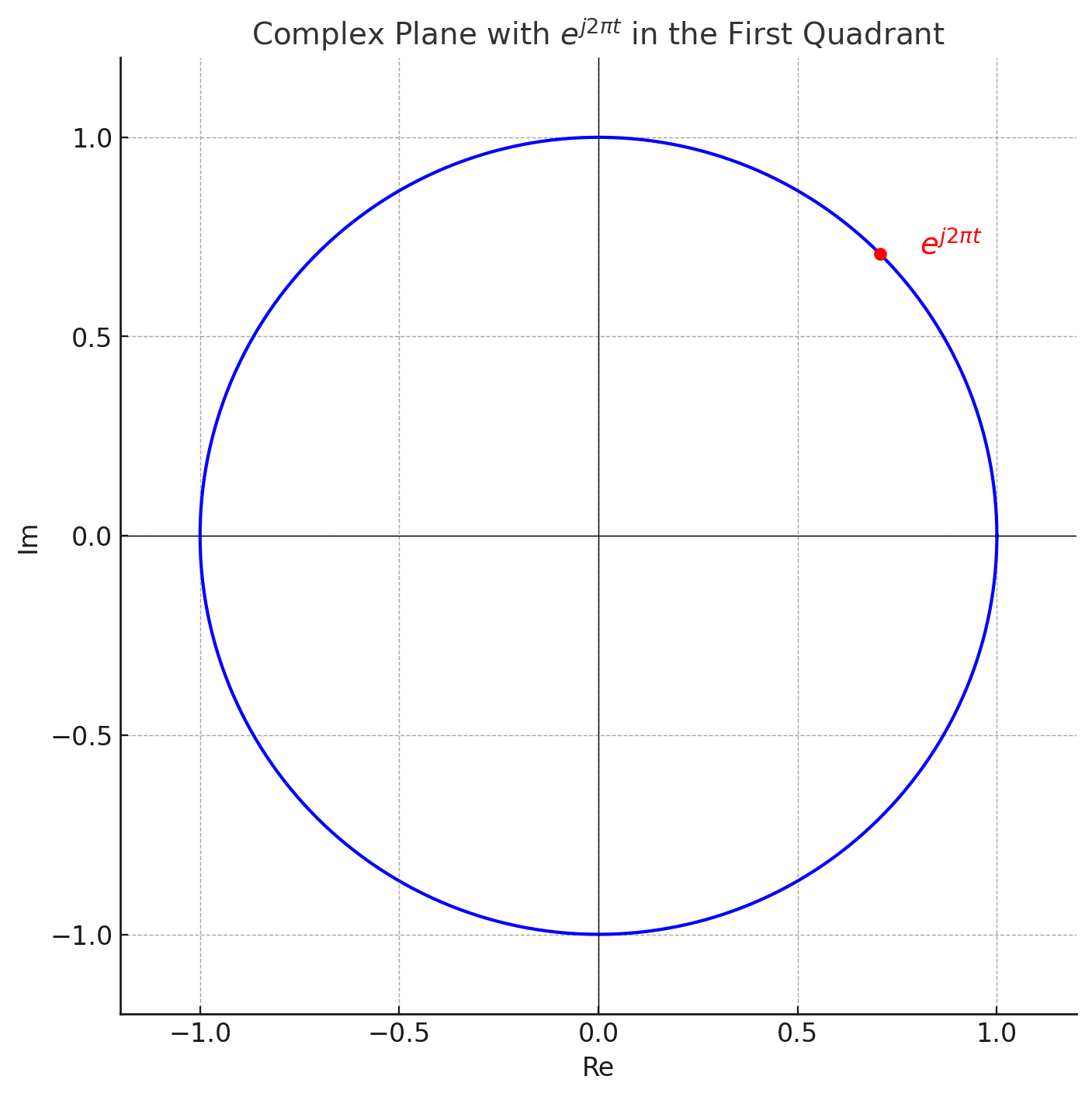
• 이 $e^{j2\pi t}$의 지수를 $-$로 해서 시계방향으로 회전하도록 한다. (일종의 Convention)
• 그리고 $f$를 지수에 있는 시간 $t$에 곱해서 진동수를 표시해준다.
• $e^{j2\pi ft}$에 시간 영역에서의 신호$f(t)$를 곱하면, 원에 감긴 그래프를 얻게 된다. (함수 $f(x)$와 주파수 $f$ 구분)
  $f(t)e^{j2\pi f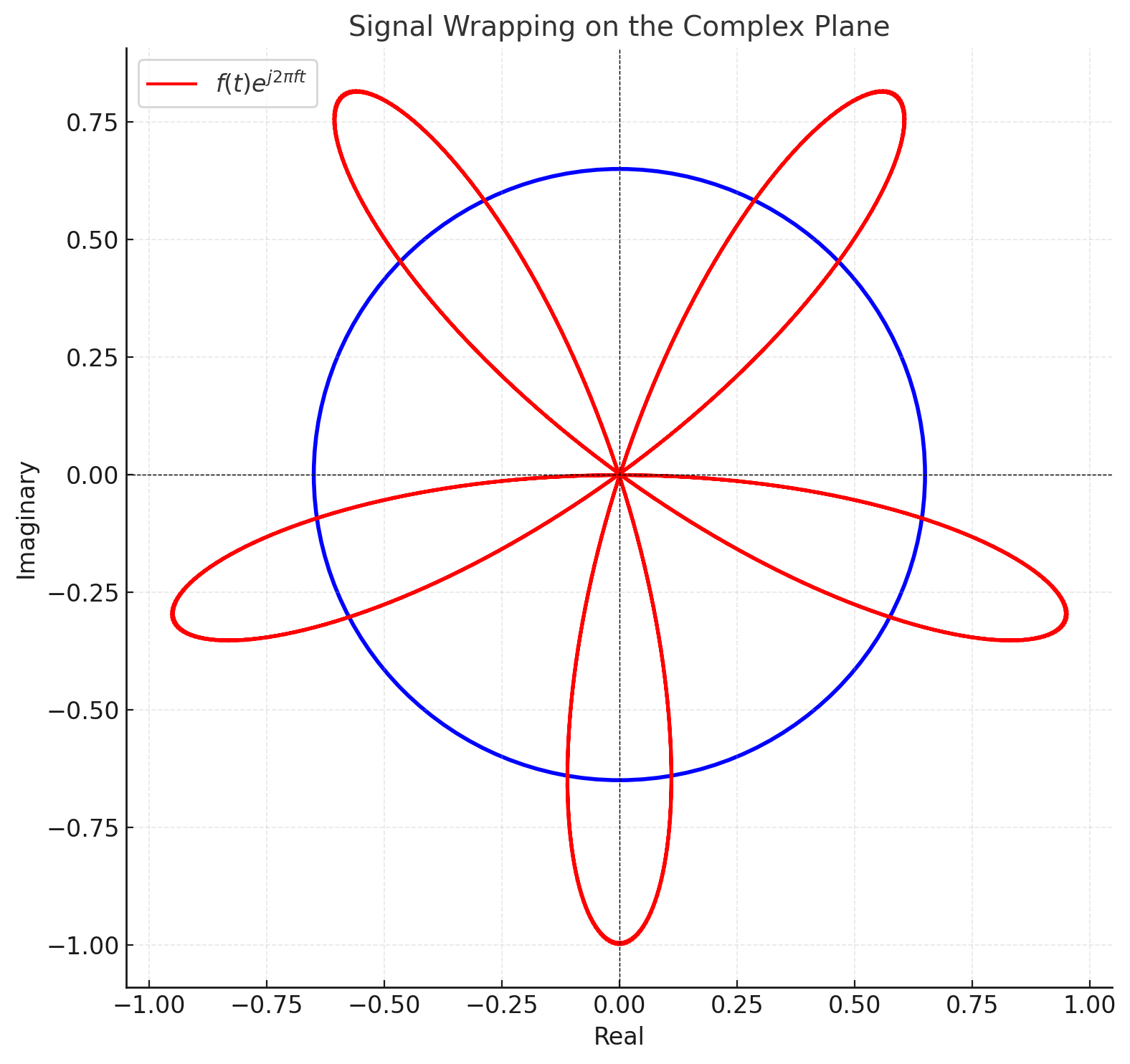t}$
  
• 이때 그래프의 무게 중심 (the center of mass)을 구하기 위해 그래프 위의 discrete 점을 n개 잡고 평균을 내면 다음과 같은 식이 된다.
  $\frac{1}{N} \sum_{k=1}^{N} f(t_k) e^{-2\pi i f t_k}$
• 점을 무수히 많이 잡으면 ($N$ tends to $\infty$)아래와 같은 식이 된다.
  $\frac{1}{t_2 - t_1} \int_{t_1}^{t_2} f(t) e^{-2\pi i f t} \, dt$
• 여기서 $\frac{1}{t_2 - t_1}$만 제거하면 푸리에 변환이 된다.
  • 따라서 엄밀히 말하면 fourier transform은 무게 중심은 아니다.
    
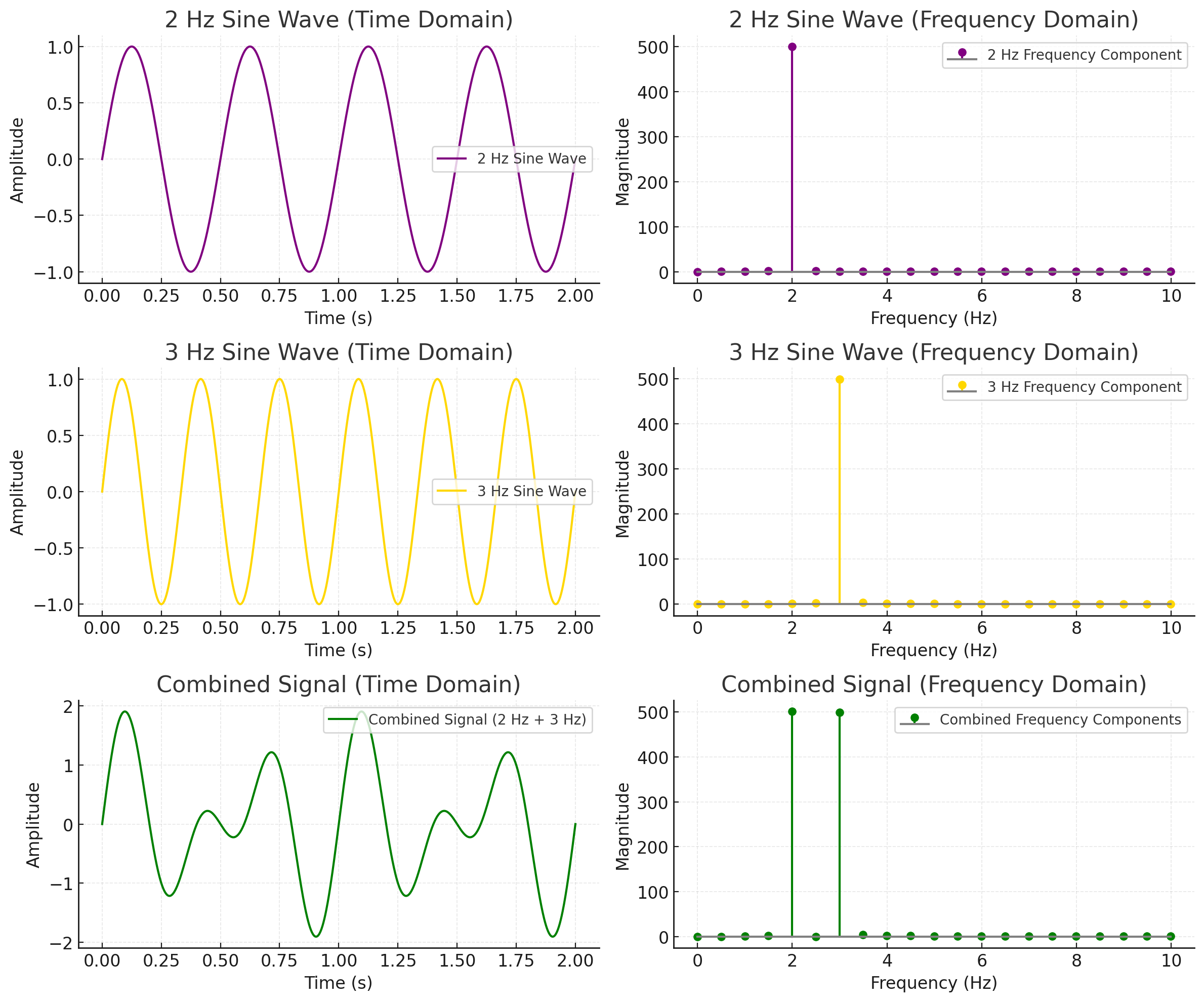
• 주파수 영역에서 $f_{rotation} = f_{signal}$일 때 나타나는 현상을 공진 현상 (Resonance)이라고 한다.
• magnitude(modulus, 절대값)
  • $\displaystyle |z|={\sqrt {x^{2}+y^{2}}}$