멀쩡한 사각형 Lv.2 | 프로그래머스

문제

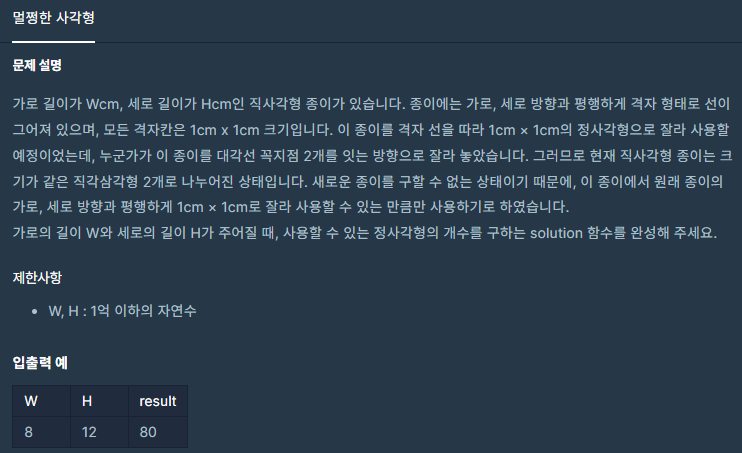
어떻게 해야할까

뭔가 옛날 초등학교 도형 문제같기도 하다.
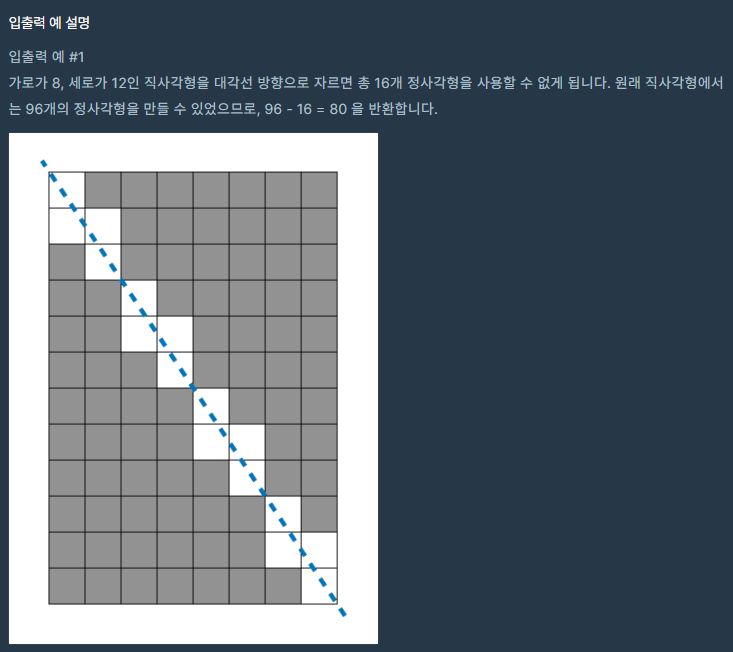
우선 가로와 세로를 곱해서 작은 정사각형의 개수를 구해야한다. 그리고 대각선으로 가로질렀을 때 몇 개의 정사각형을 못쓰는지 알아야한다.
잘 보니까 규칙은 있는 것같은데 이걸 잘 분석해보자.

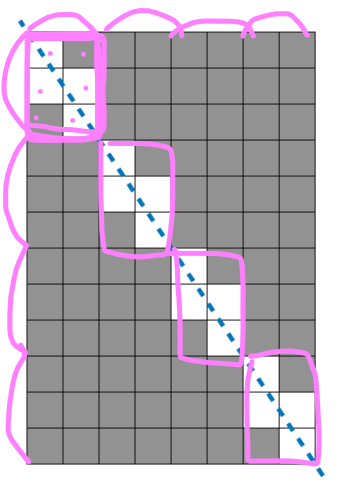
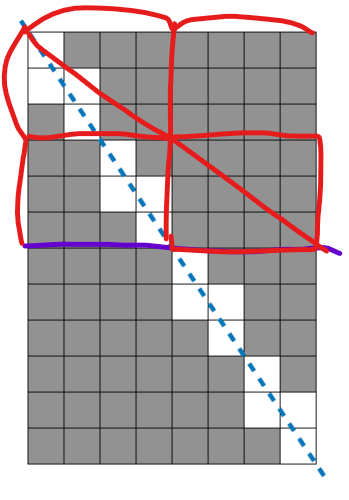
세로와 가로의 최대 공약수를 찾아서 묶....?

코드

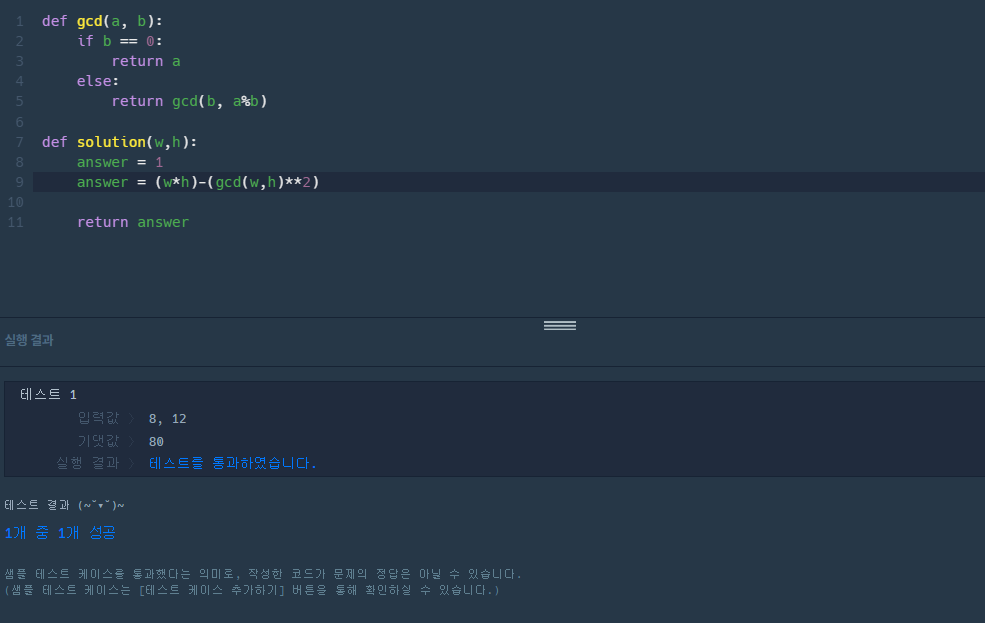
음 역시 틀렸다 ㅎㅎ 역시 알고리즘은 뚝배기 깨지는 맛으로 하지
구글링해서 보니까 최대공약수 접근은 맞는 듯 하다. 왜 항상 나는 접근만 맞고 그 다음 구현까지는 잘 안되는 걸까😂
내가 간과한 부분이 있었다.
최대공약수가 1이라면 ▶ 정확히 작은 정사각형의 대각선에 들어맞지않을 것이다.
설마 저거까지 고려해야겠어 한 내 자신이 어리석은 것이다. 그런 경우는 애매하니 입력자체를 그렇게 넣진않겠지 하고 안일하게 생각한 것이다.

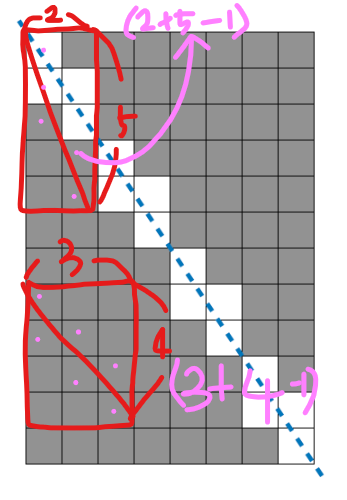
그리고 최대공약수가 1보다 클 경우는 테스트 1을 살펴보면 최대공약수가 4고 쓸수없는 정사각형의 개수가 16개다. 그래서 처음에 4의 제곱으로 생각해봤는데 그렇게 하니까 테스트케이스의 오류가 생겼다. 아까 괜히 최대공약수를 구한게 아니지않을까? 가로 세로까지 같이 생각해보면 가로(8)+세로(12)-최대공약수(4)= 20 하면 딱 떨어지게 된다.

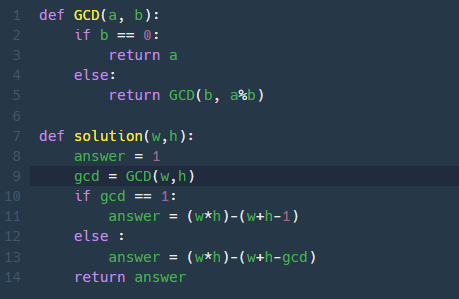
최종코드