topology sort (python)

"""
topology sort O(V+E)

DAG에만 적용이 가능하다.
(directed acyclic graph)

순서가 정해져 있는 작업을 차례로 수행해야 할 때, 
이 순서를 결정해주는 알고리즘.

In-degree = 0인 node에서 시작한다. 시작 node를 queue에 넣자.
시작 node와 연결된 다음 노드의 In-degree -= 1
이하 과정 반복.

만약, 모든 node를 방문하기 전에 queue가 비었다면 사이클이 존재한다는 것을 의미한다.
모든 원소를 반복했다면 queue에서 꺼낸 순서가 곧 sorted이다.

"""

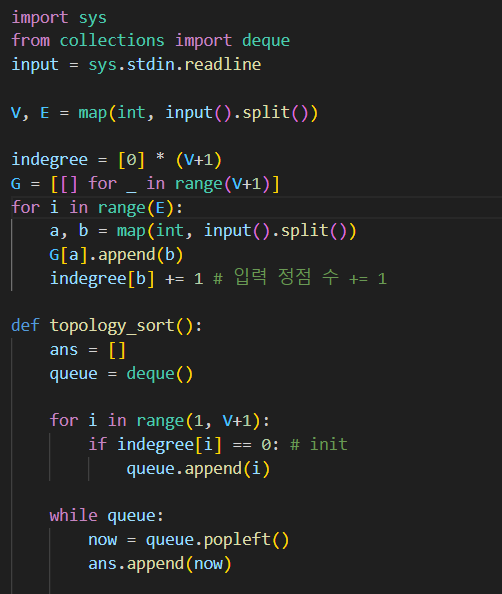
import sys
from collections import deque
input = sys.stdin.readline

V, E = map(int, input().split())

indegree = [0] * (V+1)
G = [[] for _ in range(V+1)]
for i in range(E):
    a, b = map(int, input().split())
    G[a].append(b)
    indegree[b] += 1 # 입력 정점 수 += 1

def topology_sort():
    ans = []
    queue = deque()

    for i in range(1, V+1):
        if indegree[i] == 0: # init
            queue.append(i)

    while queue:
        now = queue.popleft()
        ans.append(now)

        for next in G[now]:
            indegree[next] -= 1 # now로부터 나가는 간선 제거
            if indegree[next] == 0:
                queue.append(next)

    print(*ans)

topology_sort()

"""

example)
5 5
1 2
2 3
3 4
4 5
1 4

ans:
1 2 3 4 5

"""