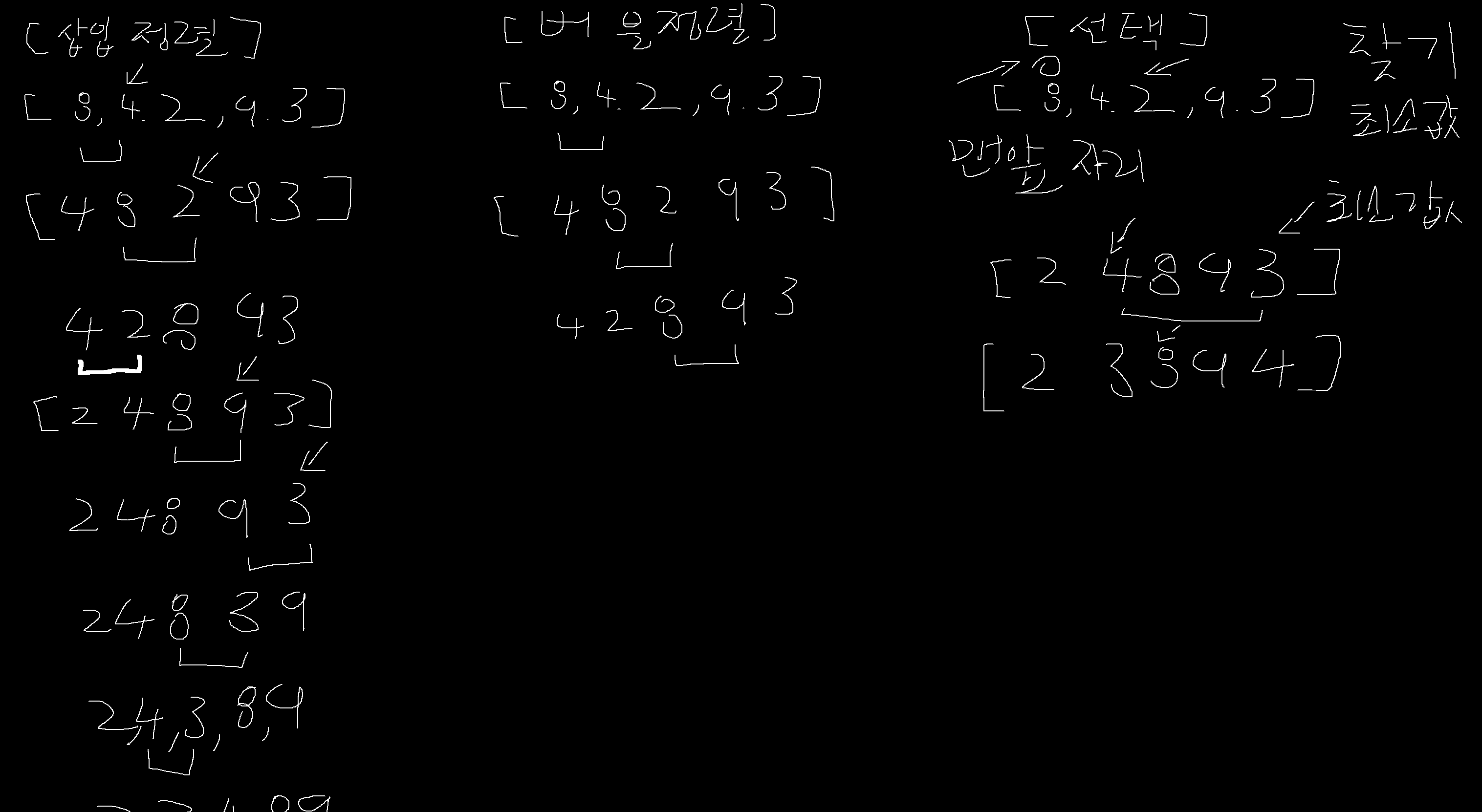-
Selection Sort [선택 정렬]
💡 선택 정렬 과정
-
주어진 리스트에서 최솟값을 찾는다.
-
최솟값을 맨 앞 자리의 값과 교환한다.
-
맨 앞 자리를 제외한 나머지 값들 중 최솟값을 찾아 위와 같은 방법으로 반복한다.
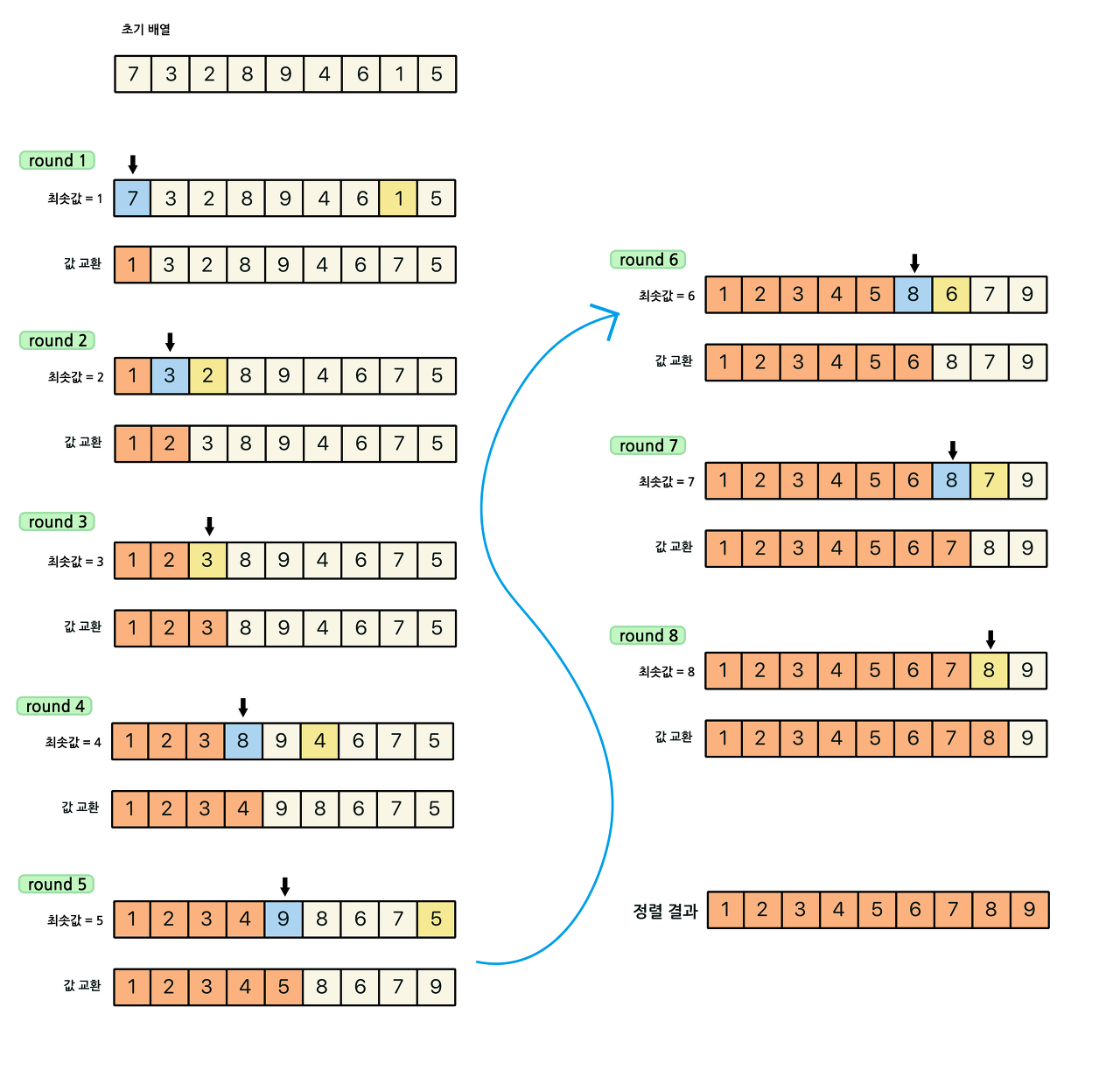
마지막 round9 를 안하는 이유는 앞 인덱스부터 순차적으로 정렬해나가기 때문에 N개의 데이터 중 N-1개가 정렬 되어있다는 것은 결국 마지막 원소가 최댓값이라는 말이고, 이는 정렬이 되어있다는 상태이므로 굳이 참조를 해줄 필요 없다
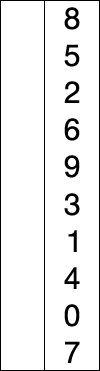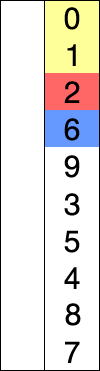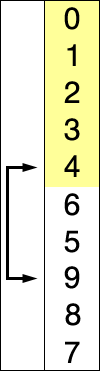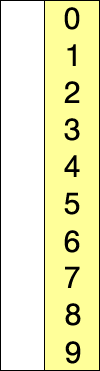

Selection 정렬 보기
-
💡 장점
- 추가적인 메모리 소비가 작다.
- 거의 정렬 된 경우 매우 효율적이다.
즉, 최선의 경우 O(N)의 시간복잡도를 갖는다. - 안장정렬이 가능하다.
💡 단점
- 역순에 가까울 수록 매우 비효율적이다. 즉, 최악의 경우 O(N2)의 시간 복잡도를 갖는다.
- 데이터의 상태에 따라서 성능 편차가 매우 크다.
🚩 단점 정리
-
첫 번째 단점이다.
기본적으로 선택정렬은 O(N2)의 시간복잡도(time complexity)를 보인다.공식을 유도해보자면 이렇다.
N이 정렬해야하는 리스트의 자료 수, i가 교환되는 인덱스라고 할 때 loop(반복문)을 생각해보자.i=1 일 때, 데이터 비교 횟수는 N-1 번 i=2 일 때, 데이터 비교 횟수는 N-2 번 i=3 일 때, 데이터 비교 횟수는 N-3 번 ⋮ i=N-1 일 때, 데이터 비교 횟수는 1 번물론 Bubble Sort 와 이론상 같은 시간복잡도를 갖음에도 비교 수행이 상대적으로 적기 때문에 조금 더 빠르긴 하나 그럼에도
좋은 알고리즘인 것은 아니다.-
두번째 단점
안정 정렬이 아니라는 것이다. 즉, Stable 하지 않다는 것. 간단한 예를 들어보겠다.우리는 다음과 같은 배열을 정렬하고자 한다.
[B1, B2, C, A] (A < B < C)
주의해서 볼 점은 B에 붙어있는 숫자는 임의로 붙인 숫자다. B1이 B2보다 크거나 작은 것이 아니라는 점 유의하길 바란다.
그럼 순서대로 순회하면서 교환한다면 이렇다.
round 1 : [A, B2, C, B1] round 2 : [A, B2, C, B1] round 3 : [A, B2, B1, C]이렇게 초기의 B1 B2의 순서가 뒤 바뀐 것을 볼 수 있다.
이러한 상태를 불안정 정렬이라고 하는데 문제가 되는 이유는
예로들어 학생을 관리하고자 할 때, 성적순으로 나열하되, 성적이 같으면 이름을 기준으로 정렬하고 싶다고 할 때.
즉, 정렬 규칙이 다수이거나 특정 순서를 유지해야 할 때
문제가 될 수 있다.[(가영, 60), (가희, 60), (찬호, 70), (동우, 45)] 이렇게 리스트가 존재한다고 생각해보자. 성적순이되, 성적이 같다면 이름순으로 정렬해야 한다고 했다.
그러면 보통 이름을 일단 정렬을 해놓을 것이다.
<이름 정렬 순>
[(가영, 60), (가희, 60), (동우, 45), (찬호, 70)]그 다음에 '성적 순'으로 정렬 할 것이다.
만약 선택 정렬을 하면 어떻게 되는지 보자.round 1 : [(동우, 45), (가희, 60), (가영, 60), (찬호, 70)] round 2: [(동우, 45), (가희, 60), (가영, 60), (찬호, 70)] round 3: [(동우, 45), (가희, 60), (가영, 60), (찬호, 70)]이렇게 '가희'보다 '가영'이 앞에 있어야 함에도
순서가 바뀌어 버린 것을 볼 수 있다.
참고 자료
-
-
Bubble Sort [거품 정렬]
💡 버블 정렬 방법
-
앞에서부터 현재 원소와 바로 다음의 원소를 비교한다.
-
현재 원소가 다음 원소보다 크면 원소를 교환한다.
-
다음 원소로 이동하여 해당 원소와 그 다음원소를 비교한다.
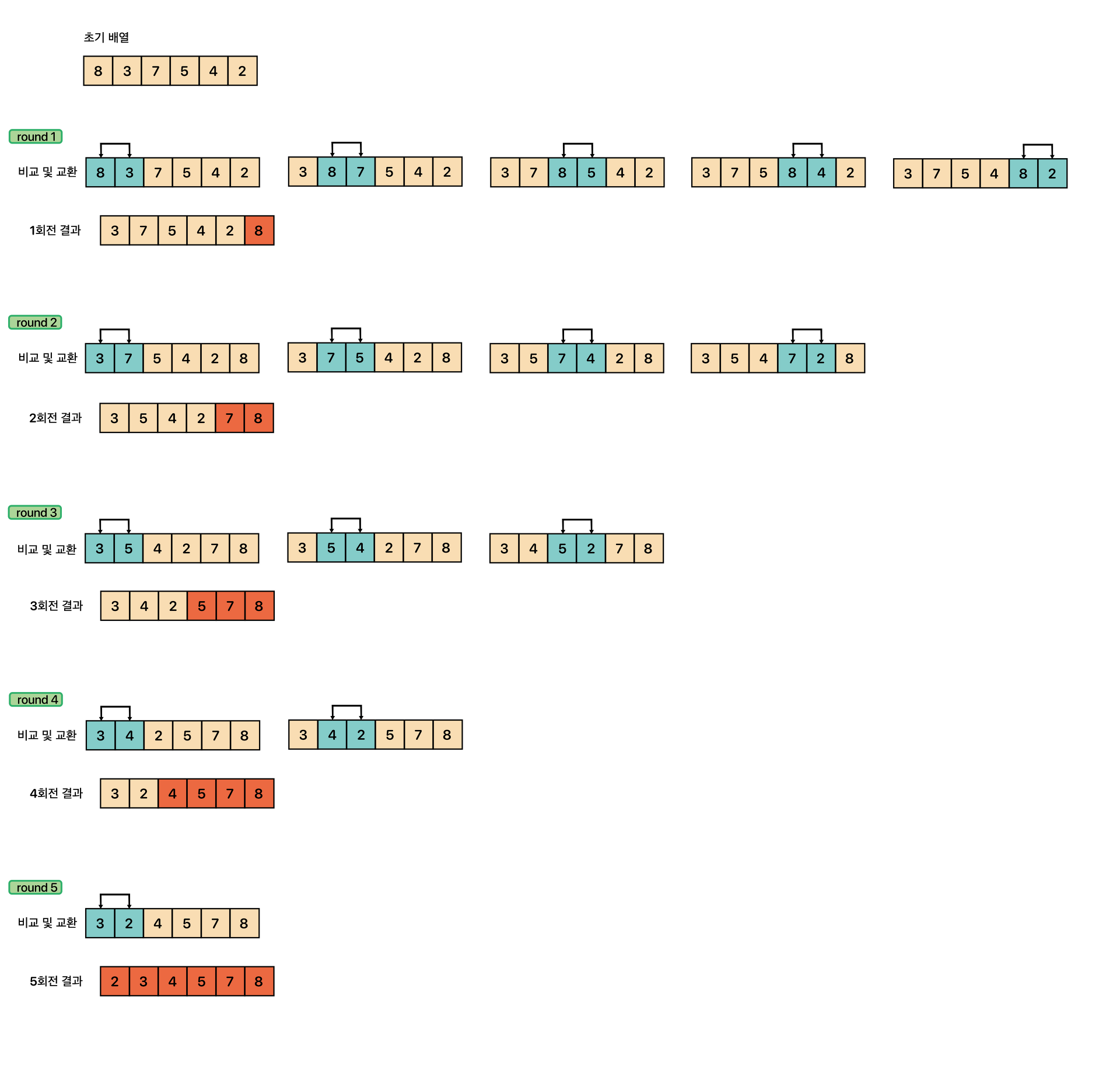
이 때, 각 라운드를 진행 할 때마다 뒤에서부터 한 개씩 정렬되기 때문에, 라운드가 진행 될 때마다 한 번씩 줄면서 비교하게 된다.한마디로 정리하자면 이렇다.
총 라운드는 배열 크기 - 1 번 진행되고,
각 라운드별 비교 횟수는 배열 크기 - 라운드 횟수 만큼 비교한다.
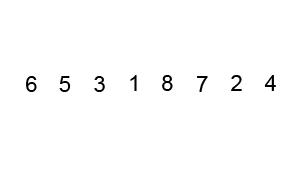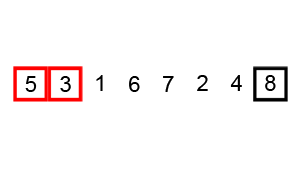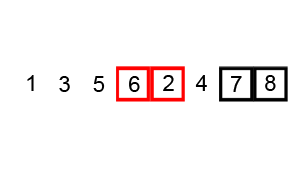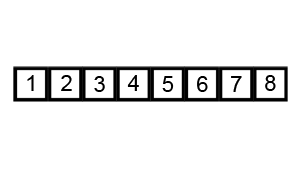

-
💡 장점
- 추가적인 메모리 소비가 작다.
- 구현이 매우 쉽다.
- 안정정렬이 가능하다.
💡 단점
- 다른 정렬 알고리즘에 비해 교환 과정이 많아 많은 시간을 소비한다.
🚩 정리
-
시간복잡도에 대해 잠깐 언급하자면, 위 알고리즘에서도 볼 수 있듯,
초기 배열에서 3과 5의 경우 원래 해당 자리에 맞는 위치지만,
교환과정에서 중간에 한 번씩 맞지 않은 자리임에도 이동하게 된다.또한 다른 정렬 알고리즘보다 값 교환 과정이 많기 때문에 그만큼 효율성도 떨어져 가장 배우기 쉽고, 구현하기 쉬움에도 사실상 쓰이지 않는 정렬 방법이기도 하다.
그럼 시간 복잡도는? 이라는 질문이라면 거품 정렬의 평균 시간 복잡도 또한 O(N2)의 시간 복잡도를 갖는다.
공식을 유도해보자면 이렇다.
N이 정렬해야하는 리스트의 자료 수, i가 라운드라고 할 때 loop(반복문)을 생각해보자.
i=1 일 때, 데이터 비교 횟수는 N-1 번 i=2 일 때, 데이터 비교 횟수는 N-2 번 i=3 일 때, 데이터 비교 횟수는 N-3 번 ⋮ i = N-1 일 때, 데이터 비교 횟수는 1 번즉, 시간복잡도는 O(N2) 이다.
참고 자료
-
Insertion Sort [삽입 정렬]
💡 삽입 정렬 방법
-
현재 타겟이 되는 숫자와 이전 위치에 있는 원소들을 비교한다. (첫 번째 타겟은 두 번째 원소부터 시작한다.)
-
타겟이 되는 숫자가 이전 위치에 있던 원소보다 작다면 위치를 서로 교환한다.
-
그 다음 타겟을 찾아 위와 같은 방법으로 반복한다.
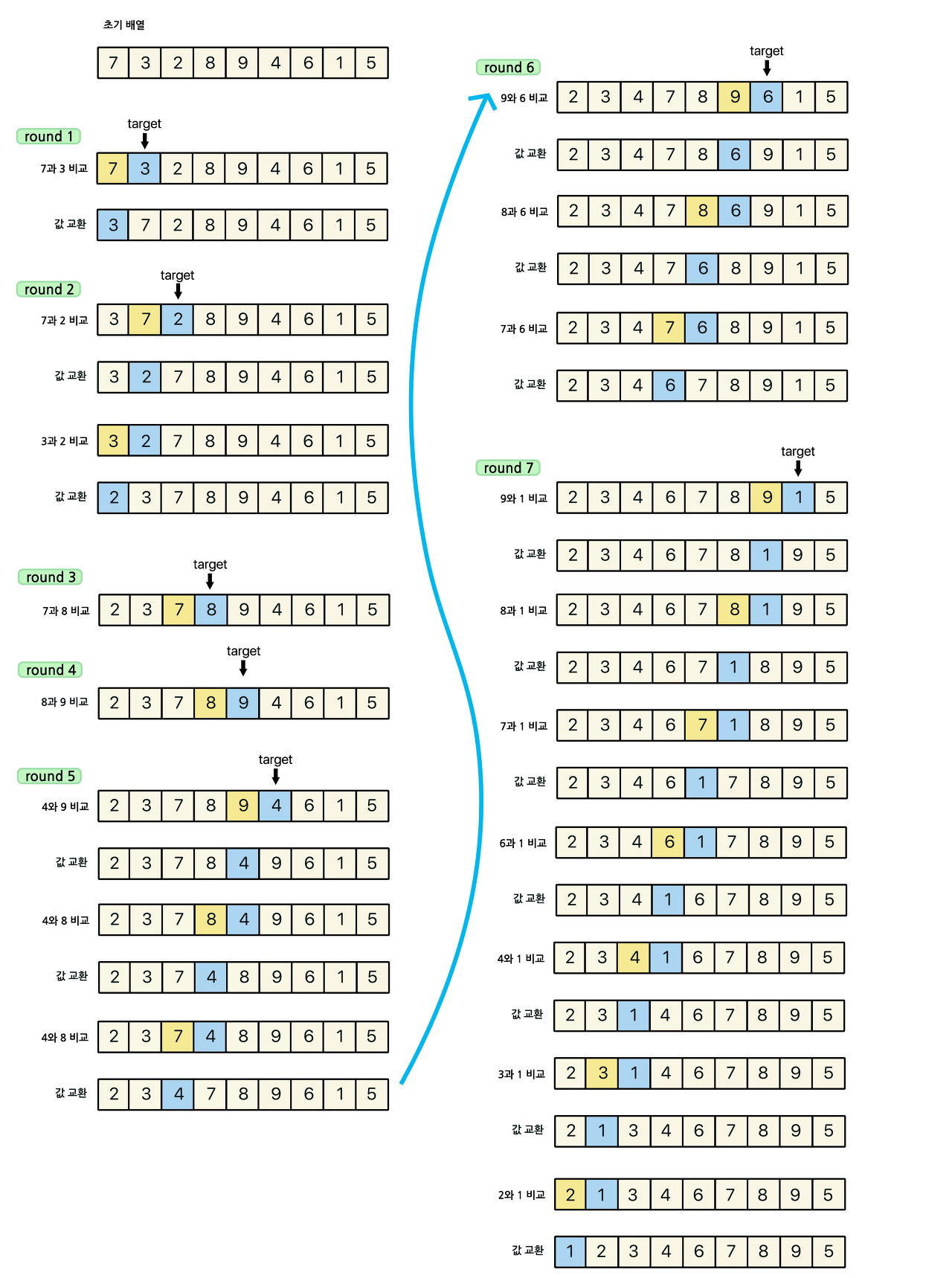
첫 번째 원소는 타겟이 되어도 비교 할 원소가 없기 때문에 처음 원소부터 타겟이 될 필요가 없고 두 번째 원소부터 타겟이 되면 된다.
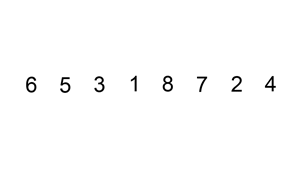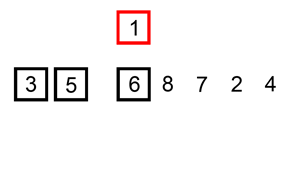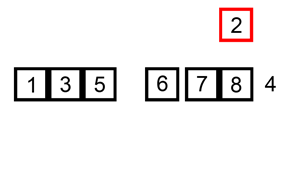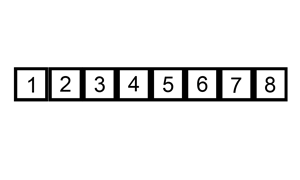

-
💡 장점
- 추가적인 메모리 소비가 작다.
- 거의 정렬 된 경우 매우 효율적이다. 즉, 최선의 경우 O(N)의 시간복잡도를 갖는다.
- 안장정렬이 가능하다.
💡 단점
-
역순에 가까울 수록 매우 비효율적이다. 즉, 최악의 경우 O(N2)의 시간 복잡도를 갖는다.
-
데이터의 상태에 따라서 성능 편차가 매우 크다.
🚩 정리
-
시간복잡도에 대해 잠깐 언급하자면, 위 알고리즘에서도 볼 수 있듯,
타겟 숫자가 이전 숫자보다 크기 전까지 반복하기 때문에 이미 정렬이 되어있는 경우 항상 타겟숫자가 이전 숫자보다 크다.
즉, 값을 N번만 비교하기 때문에 최선의 경우 O(N)의 시간 복잡도를
갖게 되는 것이다.반대로 최악의 경우는 타겟 숫자가 이전 숫자보다 항상 작기 때문에
결국 N 번째 숫자에 대하여 N-1 번을 비교해야 한다.
그렇기 때문에 최악의 경우는 O(N2)의 시간복잡도를 보인다.그럼 평균 시간 복잡도는? 이라는 질문이라면 삽입 정렬의 평균 시간 복잡도 또한 O(N2)의 시간 복잡도를 갖는다.
공식을 유도해보자면 이렇다.
이미 최선의 경우는 O(N)인 것을 알았으니 최악의 경우를 보자.
N이 정렬해야하는 리스트의 자료 수, i가 타겟이 되는 인덱스라고 할 때 loop(반복문)을 생각해보자.
i=2 일 때, 데이터 비교 횟수는 2-1 = 1번 i=3 일 때, 데이터 비교 횟수는 3-1 = 2번 i=4 일 때, 데이터 비교 횟수는 4-1 = 3 번 ⋮ i=N 일 때, 데이터 비교 횟수는 N-1 번