DFS와 BFS (python)

DFS(Depth First Search, 깊이 우선탐색)

DFS의 개념

• 그래프에서 깊은 부분을 우선적으로 탐색하는 알고리즘
• 가장 마지막에 만났던 갈림길의 정점으로 되돌아가서 다시 깊이 우선 탐색을 반복해야 하므로 후입선출 구조의 stack 사용

DFS 동작과정

1. 탐색 시작 노드를 스택에 삽입하고 방문처리
2. 스택의 최상단 노드에 방문하지 않은 인접 노드가 있으면 그 인접 노드를 스택에 넣고 방문처리
   2-1. 방문하지 않은 인접 노드가 없다면 스택에서 최상단 노드를 꺼냄
3. 2번 모든 노드를 방문할 때까지 반복

• 방문 노드를 담는 스택은 결국 비어있어야 한다.

DFS 기본적인 문제와 코드

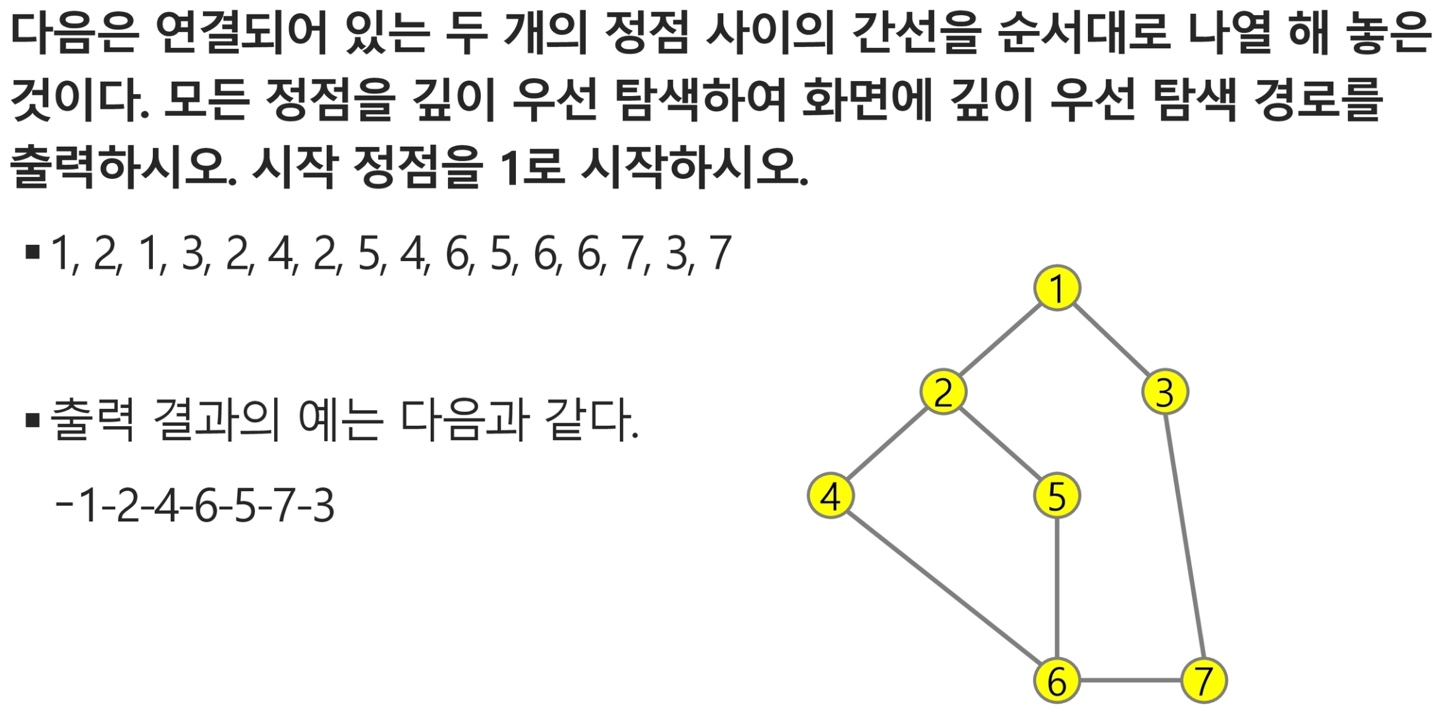
def DFS(node):
    stack=[node]
    visited=[0]*(V+1)

    while stack:
        start=stack.pop()
        if visited[start] ==0:
            visited[start]=1
            print(start, end=' ')
        for next in range(V,0,-1):
            if G[start][next]==1 and visited[next]==0:
                stack.append(next)    


V, E = map(int,input().split())
data = list(map(int, input().split()))

G=[[0] *(V+1) for _ in range(V+1)]

for i in range(0,E*2,2):
    G[data[i]][data[i+1]] =1
    G[data[i+1]][data[i]] =1

DFS(1)    

DFS 재귀

def DFS(node):
   
   
    visited[node]=1
    print(node,end=' ')
    for next in range(V+1):
        if G[node][next]==1 and visited[next]==0:
            DFS(next)


   

V, E = map(int,input().split())
data = list(map(int, input().split()))
visited=[0]*(V+1)
G=[[0] *(V+1) for _ in range(V+1)]

for i in range(0,E*2,2):
    G[data[i]][data[i+1]] =1
    G[data[i+1]][data[i]] =1

DFS(1)    

BFS(Breadth First Search, 너비 우선탐색)

BFS 개념

• 그래프에서 시작 노드에 인접한 노드부터 탐색하는 알고리즘
• 주로 간선의 비용이 동일한 조건에서 최단거리를 구할 때 효과적인 알고리즘
• 선입선출 형태의 자료구조인 큐를 활용함

BFS 동작과정

1. 탐색 시작 노드 정보를 큐에 삽입, 방문처리
2. 큐에서 노드를 꺼내 방문하지 않는 인접 노드 정보를 모두 큐에 삽입하고 방문처리.
3. 2번 과정을 더 이상 수행할 수 없을 때까지 반복.

BFS 기본적인 문제와 코드

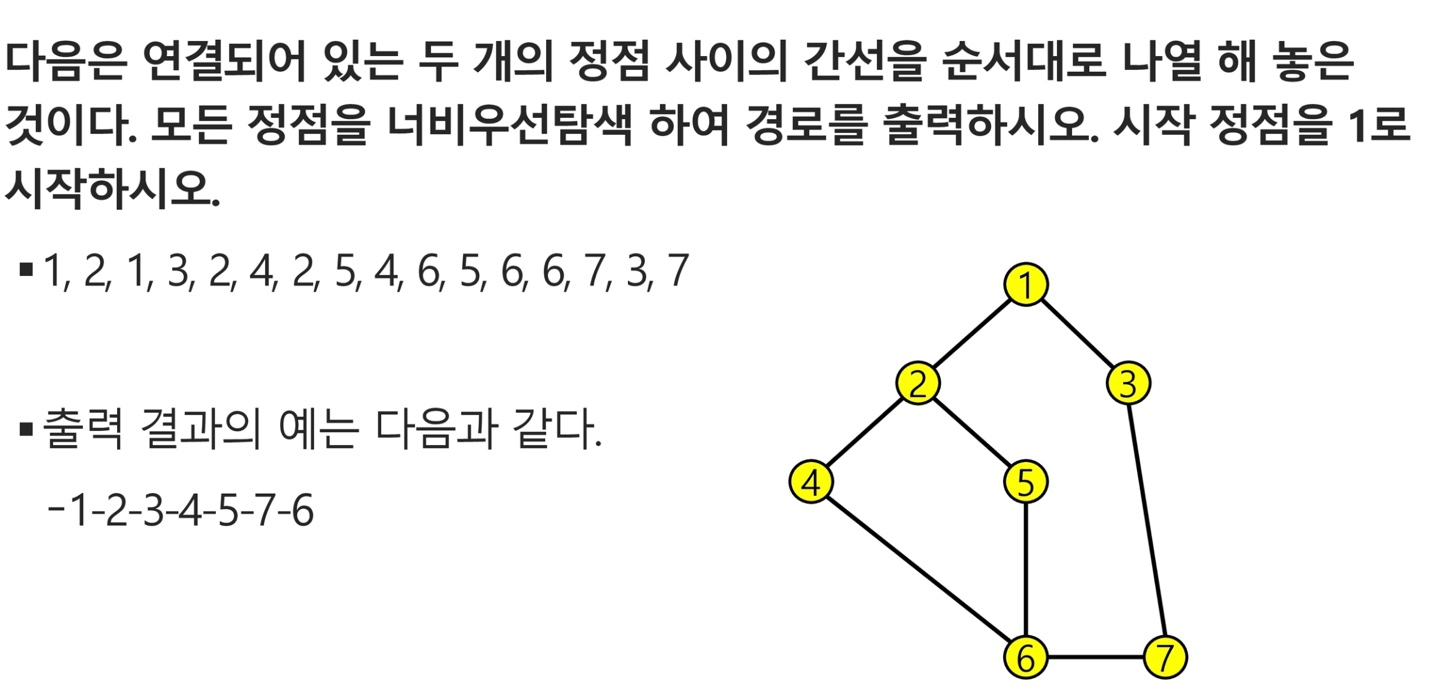
def BFS(node):
    queue = [node]
    visited = [0] * (V + 1) 
    while queue:
        start = queue.pop(0)  
        if visited[start] == 0:
            visited[start] = 1  
            print(start, end=' ')
            for next in range(V+1):
               
                if matrix[start][next] == 1 and visited[next] == 0:
                    queue.append(next)

V, E = map(int, input().split())
data = list(map(int, input().split()))

matrix = [[0] * (V + 1) for _ in range(V + 1)]

for i in range(0, E * 2, 2):
    matrix[data[i]][data[i + 1]] = 1
    matrix[data[i + 1]][data[i]] = 1
BFS(1)