최소 스패닝 트리 [BOJ1197]

문제

가중치 무향 그래프가 있을때, 해당 그래프의 모든 노드를 연결하는 최소한의 가중치 합의 트리를 구하시오.
각 가중치는 음수일 수 있고 1,000,000 이내의 절댓값을 가진다. 노드는 1만개 이하 간선은 10만개 이하다.

이해

1. 시작노드가 중요한가.

   어차피 모든 노드를 방문해야하므로 상관 없을 것 같다.

2. 아무노드를 시작노드로 잡았다.이젠 뭐하지

   연결된 거중에 하나를 골라야하는데, 기준이 없다. 이방법은 아니다.

3. 플로이드 와샬로 모든 노드 사이의 거리를 구해놓는다면?

   완전탐색 마인드로 생각해본다면, … 이건 좀 아닌듯.

완전탐색은 어떻게 하는가

그냥 DFS 때리고 백트래킹 때리면서 최소 가중치 찾아야할듯 하다.

당연히 시간초과일텐데, 그래도 생각해본 이유는 완전탐색에서 경우를 줄이거나 변화를 주는 풀이일지 고민해보기 위해서이다.

가지치기를 굳이굳이 하겠다면, 플로이드 와샬로 구한 최단거리보다 더 긴 간선을 가진 가지는 더 이상 볼 필요가 없다. 이것만으로 시간 단축이 충분할지는 모르겠다.

모르겠다했지만사실맞는듯

플로이드 와샬의 정의를 다시 생각해보니, 두 노드 사이의 최단거리이다. 어차피 최소 스패닝 트리는 어떤 두 노드도 직간접적으로 연결되어 있어야 한다. 직접 연결한 거리 == 플로이드거리 라면 두 노드를 연결하지 않을 이유가 없다. 앗 이런 만약 a-b = 6 a-c=4 c-b =2 이라면 어떡하지. 이때는 ab사이의 플로이드 거리와 직접거리가 같지만 c를 경유해서 가는게 이득이다.

위와 같은 풀이의 문제점.

1. 같은 거리일때, 여러 노드가 연결된게 이득인것을 구분하지 못한다. 이거 때문에 두 노드사이에 연결된 간선의 개수도 고려할 사항으로 넣어야할까 하다가 이건 좀 아니다를 깨달았다.
2. 간선이 음수이면 여러 간선을 연결하는 것이 가중치를 줄이는 방향이다.

나는 바보야

일단 트리형태를 구해야한다. 모든 음수 간선을 선택한다는 건 사이클을 고려하지 않은 바보같은 소리였다.

1. 가중치가 낮은 간선을 골라야한다.
2. 사이클이 생기면 안된다.
3. 간선의 개수는 상관 없다. 어차피 어떻게 골라도 트리의 간선의 개수는 n-1이다.

찾아보니 크루스칼 알고리즘이다. 이 알고리즘의 정당성을 증명해보자.

크루스칼 알고리즘

gpt의 힘을 빌려서 알고리즘의 정당성을 알아보자.

1. 탐욕적 선택 속성: 크루스칼 알고리즘에서는 각 단계마다 가장 가중치가 낮은 간선을 선택합니다. 이러한 탐욕적 선택이 최종적으로 최소 스패닝 트리를 이끌어낸다는 것이 탐욕적 선택 속성입니다. 사이클이 생성되지 않는 한, 가장 가중치가 낮은 간선은 항상 최소 스패닝 트리의 일부가 될 수 있습니다.
2. 최적 부분 구조: 크루스칼 알고리즘에서 만들어진 부분 스패닝 트리는 그 자체로도 최소 스패닝 트리의 일부입니다. 즉, 문제의 최적 해결책이 그 부분 문제의 최적 해결책으로부터 구성될 수 있다는 것을 의미합니다. 이는 각 단계에서의 최적의 선택이 최종적인 결과도 최적임을 보장합니다.

이러한 두 가지 성질을 바탕으로 크루스칼 알고리즘이 작동하는 방식은 다음과 같습니다.

각 단계에서 가장 가중치가 낮은 간선을 선택합니다. 이 간선은 사이클을 형성하지 않으므로, 이 선택은 항상 안전합니다.이 과정을 모든 간선에 대해 반복하면, 얻어진 스패닝 트리는 모든 정점을 포함하고, 가중치의 합이 최소입니다.

항상 의심해!!

1. 2번째로 작은 간선을 선택하는 것보다 3번째 4번째 간선을 선택하는게 이득일 수 도 있지 않아? 3개 다 음수 & 가중치2 > 가중치3 + 가중치4 인 경우 & 2를 선택한다면 3이나 4를 선택하지 못하는 경우 말이야.

크루스칼알고리즘에서 간선을 선택하지 못하는 이유는 사이클이 생겨서이다. 사이클이 생기려면 (두 노드 사이의 간선이 2개 이상이 존재하지 않는 한) 3개의 간선이 존재해야한다. 이 간선의 각각은 가중치2보다 클 것이므로 다른 대안의 일부만 고르면 사이클도 안생기고 이득도 볼 수 있다.

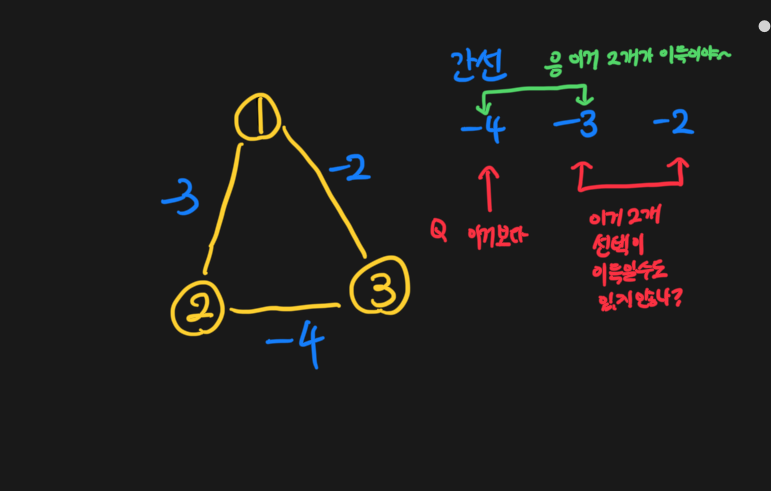
2. 사이클을 피해서 만들다보면 모든 노드가 연결된다는 보장이 있냐?

사실 너무 당연하다. 모든 노드 사이의 임의의 경로가 존재한다고 했기 때문에, 문제에서 제시되는 그래프는 (어떤한 관점에서든) 최소한의 트리에 사이클을 만드는 간선을 추가했다고 볼 수 있다. 그러므로 그 역과정인 사이클을 만드는 간선들을 배제하며 구성한다면 모든 노드는 연결될 것이다. 사이클을 만드는 간선은 어차피 이미 연결된 두 노드를 다시 연결하는 간선이므로 필요가 없다.

3. a b c d 순서일때 a를 고르지 않고도, 모든 노드가 연결되며 더 최소 가중치를 만들 수 있는 방법은 없는가?

임의의 두 노드를 직접 연결하는 간선은 하나밖에 존재하지 않는다. 그러므로 a 이후에는 a의 양쪽 두 노드를 연결하는 노드는 존재하지 않는다. 그렇다면 이제 간접적으로 연결하는 수 밖에 없다. b + c 는 a보다 클 수 밖에 없으므로 반례는 존재하지 않는다.

자 이제 어쩔래

1. 각 간선을 가중치에 따라 오름차순으로 정렬합니다.
   1. vector<가중치, <from,to>>로 자료구조를 잡고, 가중치를 기준으로 정렬하자.
2. 가장 가중치가 낮은 간선부터 순서대로 트리에 추가합니다.
   1. for문으로 vector를 순회하며 from과 to의 isInTree 값을 true로 만들어준다.
3. 간선을 추가할 때, 해당 간선이 사이클을 형성하는지 확인합니다. 사이클을 형성한다면 그 간선은 제외합니다.
   1. 이미 isInTree라면 skip한다.
4. 모든 노드가 연결될 때까지 이 과정을 반복합니다.
   1. 그냥 for문 다하면 된다.

네 틀렸구요.

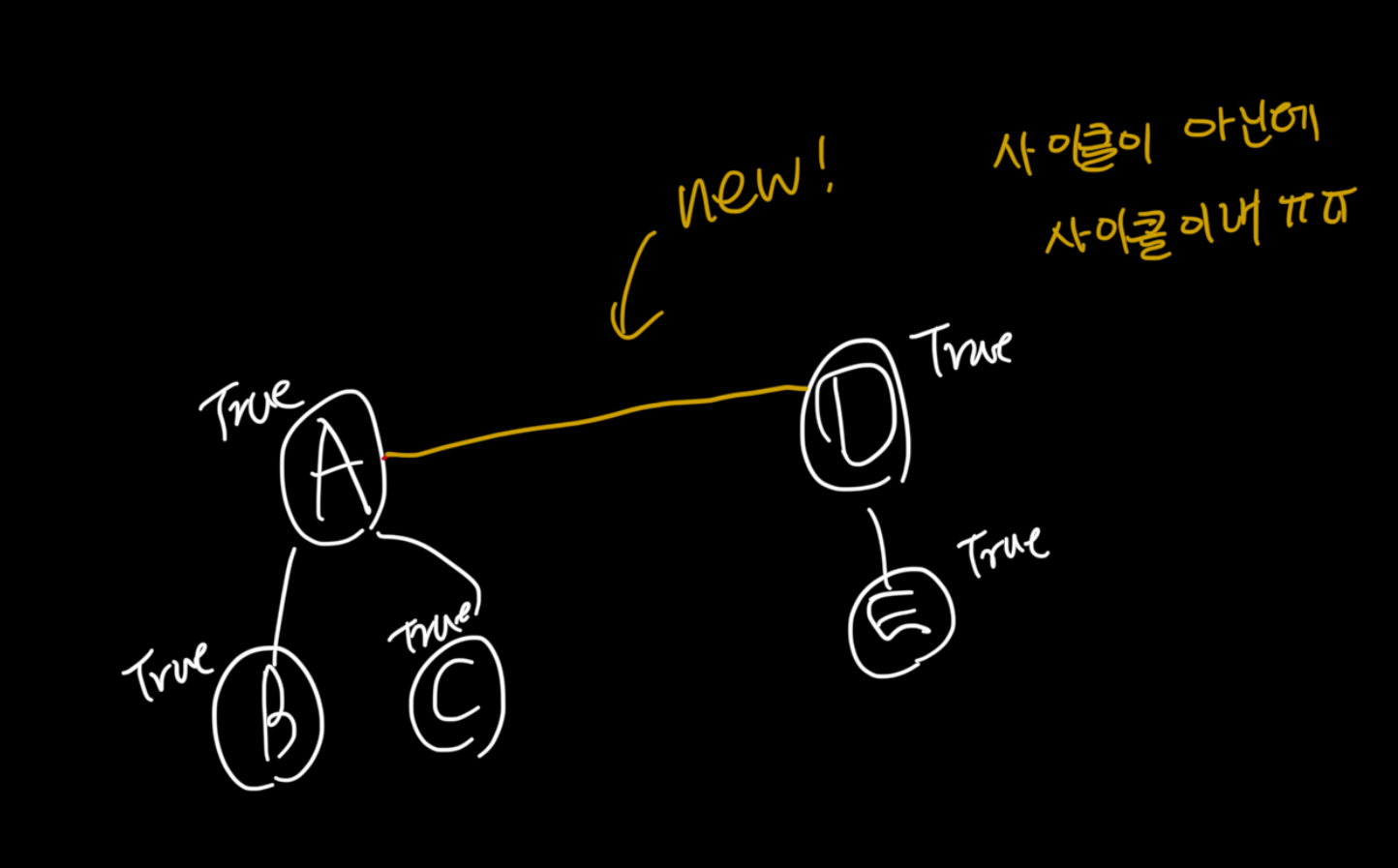
시원한 반례입니다. 너무 뇌를 빼버린것 같군요. 추가하려는 간선이 사이클을 만드는지 판단하기 위해서는 두 노드의 조상 노드가 같은지 확인해야한다. (또는 DFS하거나ㅋㅋ) 매번 조상을 하나하나 타고 올라가며 계산하기는 어려우므로 유니온 파인드를 활용하자.

유니온 파인드

void find(vector<int>& parent, int i ){
	if(parent[i] == i) return i;
	return find(parent, parent[i]);
}
void Union(vector<int>& parent, int x , int y){
	int xDes = find(parent, x);
	int yDes = find(parent, y);
	if( xDes != yDes ) parent[xDes] = yDes;
}

parent[i] = (현재까지 중의 ) i 번 노드의 최대 조상.

find 메서드 → 재귀적으로 자신의 조상을 찾는다.

union 메서드 → 두 노드의 조상노드를 찾아서, 한쪽을 하나의 자식으로 편입시킨다.

시간초과 해결

union을 할때, 두 노드 중 어떤 노드를 자식으로 둘지 정하지 않는다면 시간초과를 피할 수 없었다. 그냥 일단 감으로 두 트리가 합쳐질 때, 루트노드가 큰게 합쳐진 트리의 루트가 된다고 풀었더니 해결되었다. 왜 그럴까.

find에서 시간이 오래걸리는 이유는 parent[i]가 현재 나의 조상과 너무 멀기 때문이다. 타고 올라갈 산이 많은 거다.

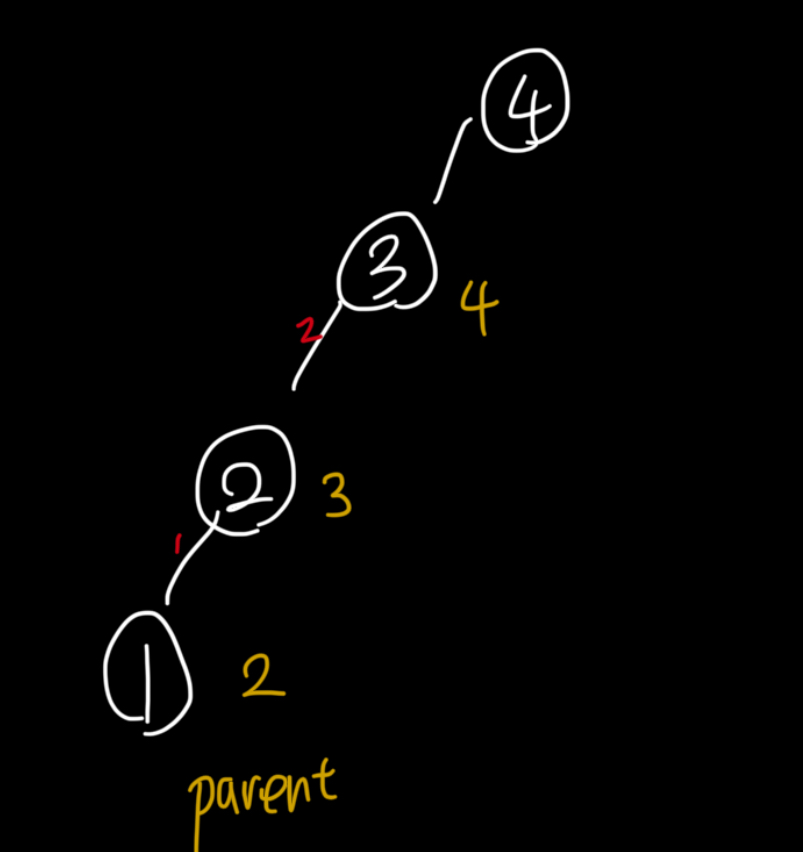
아래 그림에서 1번 노드가 자신의 조상을 찾기 위해서는 총 3번의 재귀호출이 필요하다. 이것이 시간초과를 만든다. 그러므로 우리는 하나의 노드에 최대한 많은 노드가 직접적으로 연결되면 좋겠다. 가능하다면 조상을 빨리찾도록.

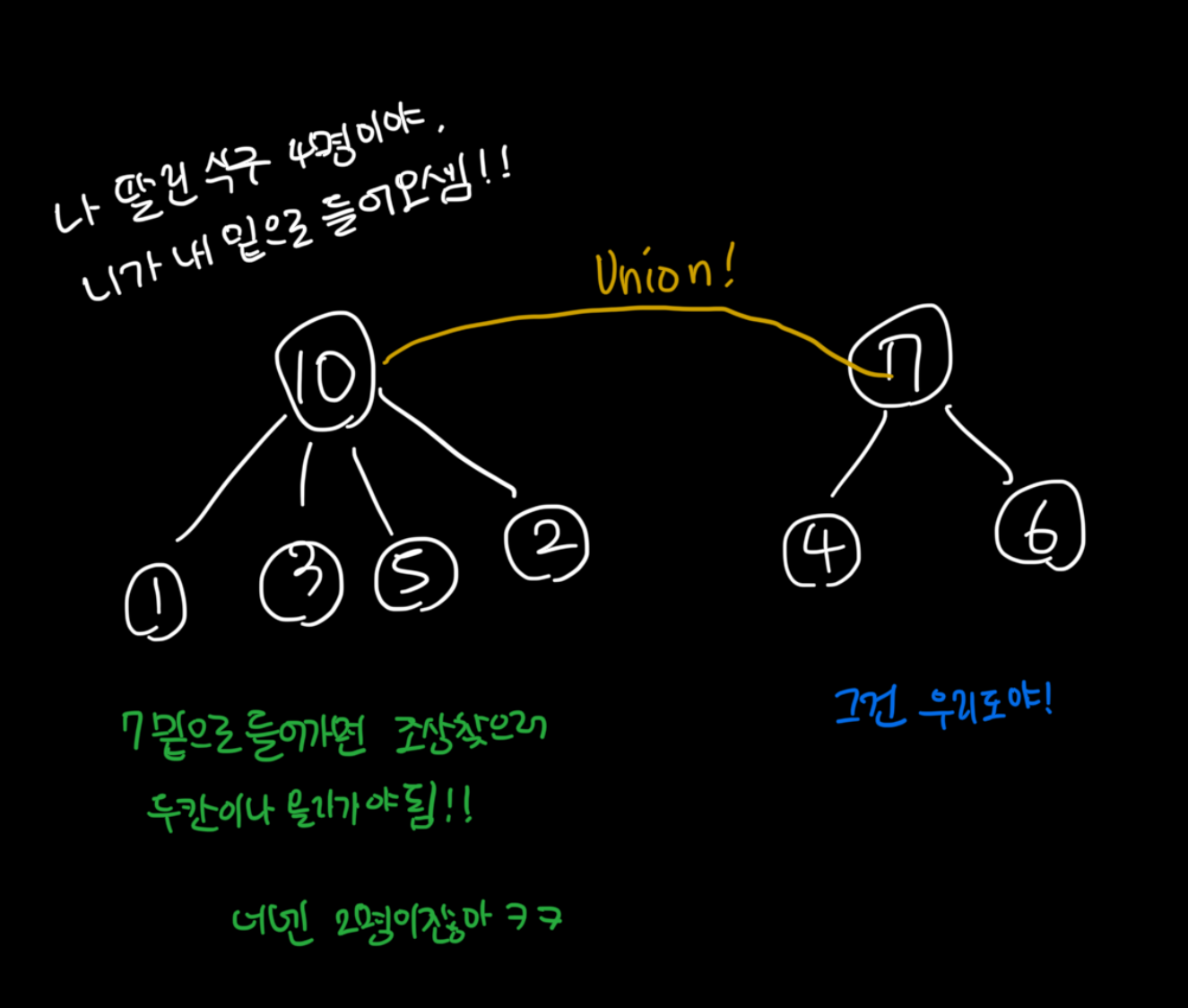
자식이 4명이 노드와 자식이 2명인 노드가 있다. 여기서 합칠때, 7이 10의 자식으로 들어가 4와 6만 2칸 올라가는 수고로움을 감수한다면 1,2,3,5는 union 후에도 한번에 조상노드를 찾을 수 있다.

그러니까 결국 자식노드가 많은 루트노드가 합쳤을때의 루트노드가 되는게 맞다. 하지만 이렇게 하려면 자식노드의 개수를 관리하는 vector가 하나 더 필요하고 귀찮아지므로 대충 생각해보자. 입력으로 들어오는 간선은 대체로 무작위 할 것이다. 그리고 만약 노드값이 큰것이 합쳐질때 루트가 되는 룰을 적용한다면, 7보다는 10이 더 많은 자식을 가지고 있을 확률이 높다. 그러니까 10이 이긴걸로 하자.

물론 이렇게 하면 이전 그림처럼 1-2 2-3 3-4 4-5 와 같은 입력에 대해서는 최악의 시간복잡도를 보여줄 것이다.
하지만 난 무작위를 믿고 그냥 했다.

code

#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;

// 간선을 표현하는 구조체
struct Edge {
    int src, dest, weight;
};

// 유니온-파인드 알고리즘을 위한 함수들
int find(vector<int>& parent, int i) {
    if (parent[i] == i) return i;
    return find(parent, parent[i]);
}

void Union(vector<int>& parent, int x, int y) {
    int xset = find(parent, x);
    int yset = find(parent, y);
    if(xset < yset) parent[xset] = yset;
    if(xset > yset) parent[yset] = xset;
}

// 크루스칼 알고리즘
int kruskalMST(vector<Edge>& edges, int n) {
    int mst_weight = 0;

    // 간선들을 가중치 기준으로 정렬
    sort(edges.begin(), edges.end(), [](const Edge &a, const Edge &b) {
        return a.weight < b.weight;
    });

    vector<int> parent(n + 1);
    for (int i = 1; i <= n; ++i) parent[i] = i;

    for (Edge &edge : edges) {
        int x = find(parent, edge.src);
        int y = find(parent, edge.dest);

        if (x != y) {
            mst_weight += edge.weight;
            Union(parent, x, y);
        }
    }

    return mst_weight;
}

int main() {
		ios_base::sync_with_stdio(false);
    cin.tie(NULL);
    int n, m;
    cin >> n >> m;

    vector<Edge> edges(m);
    for (int i = 0; i < m; ++i) {
        cin >> edges[i].src >> edges[i].dest >> edges[i].weight;
    }

    cout << kruskalMST(edges, n) << endl;

    return 0;
}

구조체랑 sort

vector pair pair int int int 하기 귀찮아서 gpt한테 부탁했더니 오랜만에 구조체를 보게되었다.

자주 애용해야겠따. 그리고 저 sort부분은 익명함수이다. []는 람다 소개자로 매개변수 이외의 외부변수를 사용해야할때 사용한다고 한다. 매개변수로 const로 sort과정에서 값이 변경되지 않음을 보장하고 객체의 참조를 사용한다.