에지 리스트(Edge List)
에지 리스트는 에지를 중심으로 그래프를 표현
배열에 출발 노드, 도착 노드, (+가중치)를 저장하여 표현할 수 있다
아래 그래프들은 유향 그래프(방향이 있는 그래프)
// 가중치가 없는 그래프
int[][] edgeList =
{
{0, 0},
{1, 2},
{1, 3},
{3, 4},
{2, 4},
{2, 5},
{4, 5}
};
// 출발과 도착, 1~5까지
// -----출력
// [1, 2]
// [1, 3]
// [3, 4]
// [2, 4]
// [2, 5]
// [4, 5]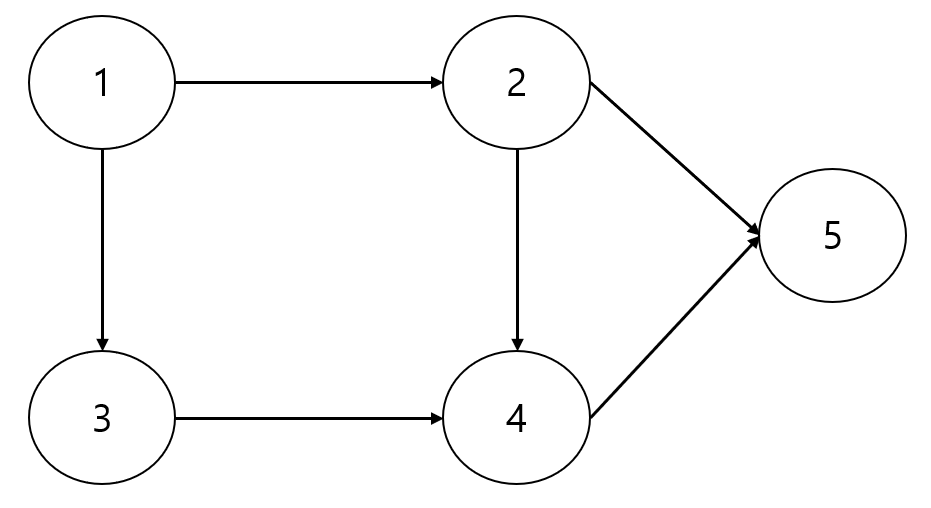
// 가중치가 있는 그래프
int[][] edgeListW =
{
{0, 0, 0},
{1, 2, 8},
{1, 3, 3},
{3, 4, 13},
{2, 4, 4},
{2, 5, 15},
{4, 5, 2}
};
// ----- 출력
// [1, 2, 8]
// [1, 3, 3]
// [3, 4, 13]
// [2, 4, 4]
// [2, 5, 15]
// [4, 5, 2]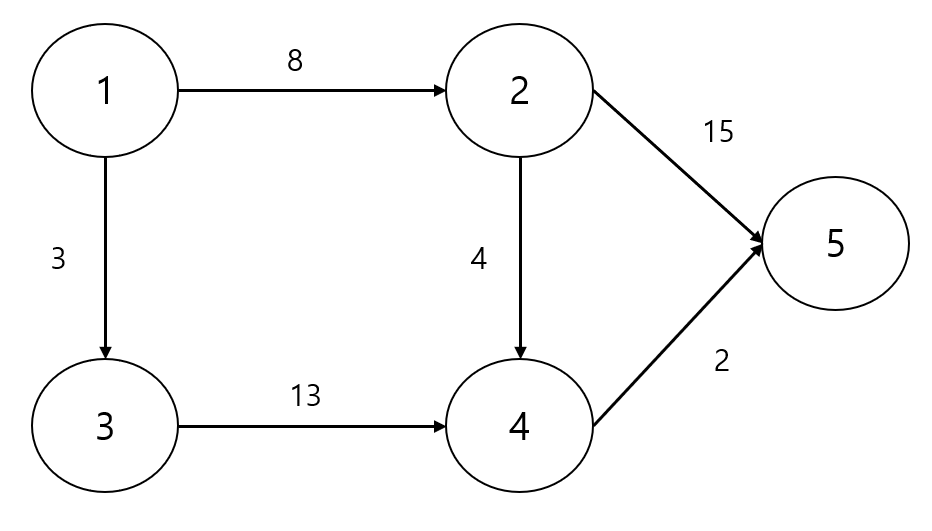
에지 리스트는 구현이 쉽다
벨만 포드, 크루스칼(MST) 알고리즘 등에 사용한다
하지만 노드 탐색이 어렵기 때문에 노드 중심 알고리즘에는 사용하기 어렵다
인접 행렬
2차원 배열을 자료구조로 이용하여 그래프 표현
노드 중심으로 그래프를 표현한다
// 가중치가 없는 인접행렬
int[][] adjMatrix = new int[6][6];
adjMatrix[1][2] = 1;
adjMatrix[1][3] = 1;
adjMatrix[2][4] = 1;
adjMatrix[2][5] = 1;
adjMatrix[3][4] = 1;
adjMatrix[4][5] = 1;
// ----- 출력
// 0 1 1 0 0
// 0 0 0 1 1
// 0 0 0 1 0
// 0 0 0 0 1
// 0 0 0 0 0 1로 표시된 부분은 연결이 된 부분이며(r -> c)로 가는 길이 있다는 의미
// 가중치가 있는 인접행렬
int[][] adjMatrix = new int[6][6];
adjMatrix[1][2] = 8;
adjMatrix[1][3] = 3;
adjMatrix[2][4] = 4;
adjMatrix[2][5] = 15;
adjMatrix[3][4] = 13;
adjMatrix[4][5] = 2;
// ----- 출력
/*
0 8 3 0 0
0 0 0 4 15
0 0 0 13 0
0 0 0 0 2
0 0 0 0 0
*/0이 아닌 곳은 연결되어 있으며, 해당 배열의 값이 곧 가중치
인접행렬의 장점
구현이 쉽다
연결 여부와 가중치를 배열에 직접 접근하면 바로 확인이 가능
인접행렬의 단점
노드와 관련되어 있는 에지를 탐색하기 위해서는 N번 접근해야 한다 -> 노드 개수에 비해 에지가 적을 때는 공간 효율성이 떨어짐
노드가 많으면 배열 선언이 힘들다
노드가 3만개 이상일 경우 자바 힙스페이스 에러(Java Heap Space Error) 발생
인접 리스트
// 가중치 없는 인접 리스트
ArrayList<Integer>[] adjList = new ArrayList[6];
for(int i = 1; i < 6; i++) {
adjList[i] = new ArrayList<Integer>();
}
adjList[1].add(2);
adjList[1].add(3);
adjList[2].add(4);
adjList[2].add(5);
adjList[3].add(4);
adjList[4].add(5);
// ----- 출력
/*
1 [2, 3]
2 [4, 5]
3 [4]
4 [5]
5 []
*/// 가중치 있는 인접 리스트
static public class Node {
int x, w;
public Node(int x, int w) {
this.x = x;
this.w = w;
}
@Override
public String toString() {
return "Node{" +
"x=" + x +
", w=" + w +
'}';
}
ArrayList<Node>[] adjList = new ArrayList[6];
for(int i = 1; i < 6; i++) {
adjList[i] = new ArrayList<Node>();
}
adjList[1].add(new Node(2, 8));
adjList[1].add(new Node(3, 3));
adjList[2].add(new Node(4, 4));
adjList[2].add(new Node(5, 15));
adjList[3].add(new Node(4, 13));
adjList[4].add(new Node(5, 2));
// ----- 출력
/*
1 [Node{x=2, w=8}, Node{x=3, w=3}]
2 [Node{x=4, w=4}, Node{x=5, w=15}]
3 [Node{x=4, w=13}]
4 [Node{x=5, w=2}]
5 []
*/ 인접 리스트의 장점
노드와 연결되어 있는 에지 탐색 시간이 좋다
공간 효율이좋아 메모리 관리도 용이
코딩 테스트에서 자주 사용된다
인접 리스트의 단점
구현이 복잡하다
인접 행렬과 인접 리스트
만일 노드의 개수가 10개라면,
인접 행렬로 작성해도 메모리 상 문제가 없을 것
하지만, 노드가 1억개, 간선 정보가 그보다 적다면?
인접 행렬로 작성한 경우 연결 정보를 찾기 위해 1억 by 1억의 배열을 전부 탐색해야 하는 경우가 생긴다
따라서 인접 리스트를 주로 활용해야 할 것
| 인접 행렬 | 인접 리스트 | |
|---|---|---|
| 검색 | O(1) | O(degree(v)) |
| 차수 계산 | O(n) | O(degree(v)) |
| 전체 탐색 | O(n^2) | O(e) |
| 메모리 | n * n | n + e |
| 구현 | 쉽다 | 어렵다 |
참고
Do it 알고리즘 코딩테스트 자바편
https://velog.io/@falling_star3
