다익스트라 알고리즘 (Dijkstra Algorithm)

ideal dev·2023년 1월 17일
다익스트라알고리즘
0

알고리즘

목록 보기
3/3
post-thumbnail

다익스트라 알고리즘이란?

그래프를 탐색하는데 최단 경로를 구해야 한다? 그럴 때 사용하는 알고리즘으로,
그래프 탐색 방법 중 하나로 최단 경로 탐색 알고리즘입니다.

  1. 어떤 그래프에 적용하냐?
  2. 최단 경로를 구하는 방법?
  3. 시간복잡도?

순으로 하나씩 살펴보도록 합시다.

1. 어떤 그래프에 적용하냐?

  • 음의 가중치가 없는 그래프에서 적용되는 방법입니다.
  • 방향은 무향,우향 둘 다 가능하며
  • 간선마다 이동거리가 존재하는 그래프에서 사용합니다.

2. 최단 경로를 구하는 방법?

  1. 초기값은 출발 정점은 0, 나머지 정점은 최단 경로를 구하지 않은 상태이므로 무한대(아주 큰 값)로 표시합니다.
  2. 아직 방문하지 않은 정점 중 거리가 가장 짧은 정점을 하나 선택해 방문합니다.
  3. 해당 정점에서 인접하고 아직 방문하지 않은 정점들의 거리를 갱신합니다.
    2,3 을 모든 정점을 반복하면 끝입니다, 간단하지요~?

💡 앞에서 생략한 설명이 하나 있는데요,
다익스트라는 다이나믹 프로그래밍을 활용한 최단 경로 탐색 알고리즘입니다.
하나의 최단 거리를 구할 때 그 이전까지 구했던 최단 거리 정보를 그대로 사용한다는 특징 때문인데요.
위의 설명 3.아직 방문하지 않은 정점들의 거리를 갱신 할 때 사용합니다.
말로만 보면 당연히 어려우니, 그래프와 함께 보며 이해해보도록 하겠습니다.

출발 정점은 1번으로 하겠습니다..
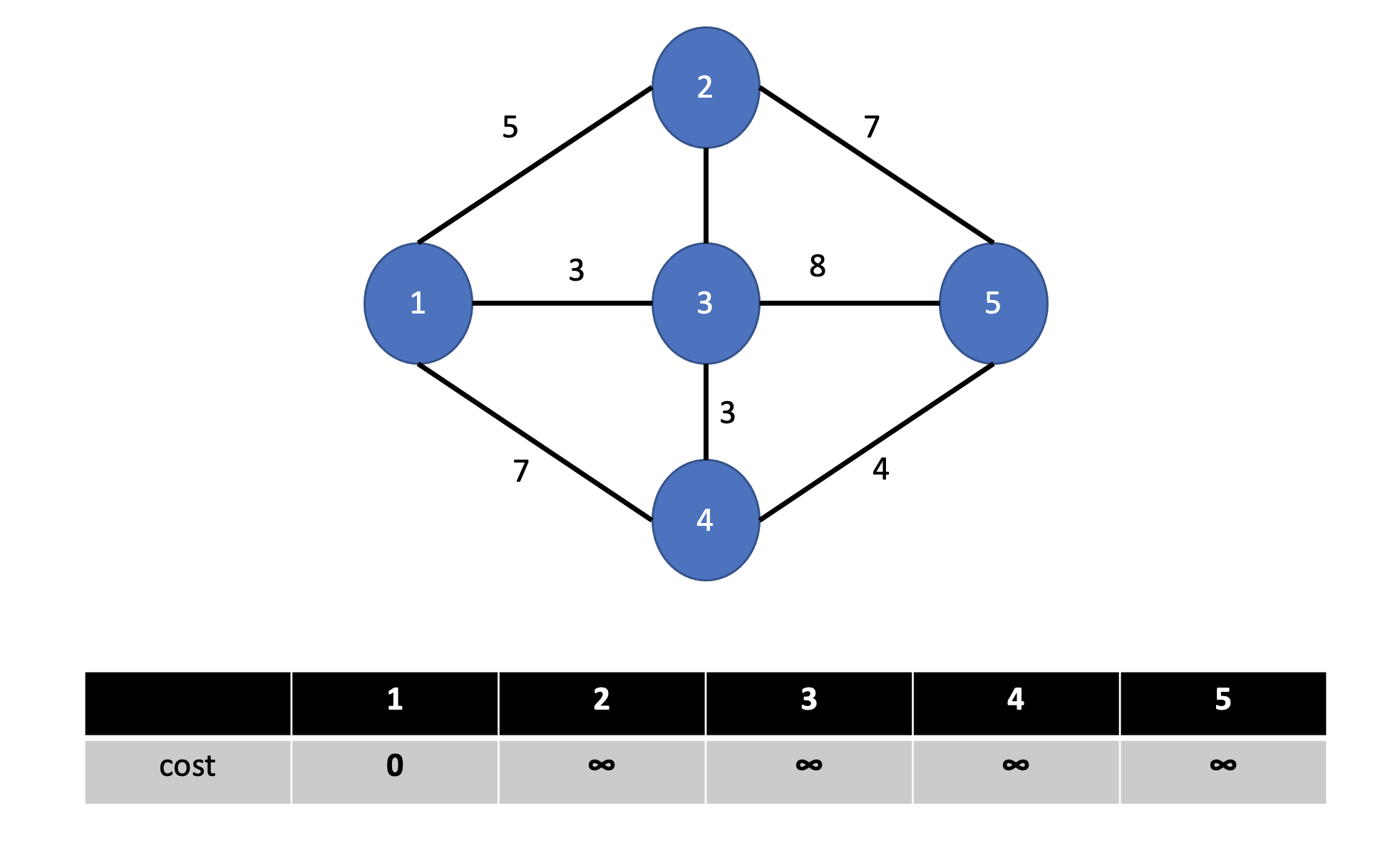
1. 초기값은 출발 정점은 0, 나머지 정점은 무한대

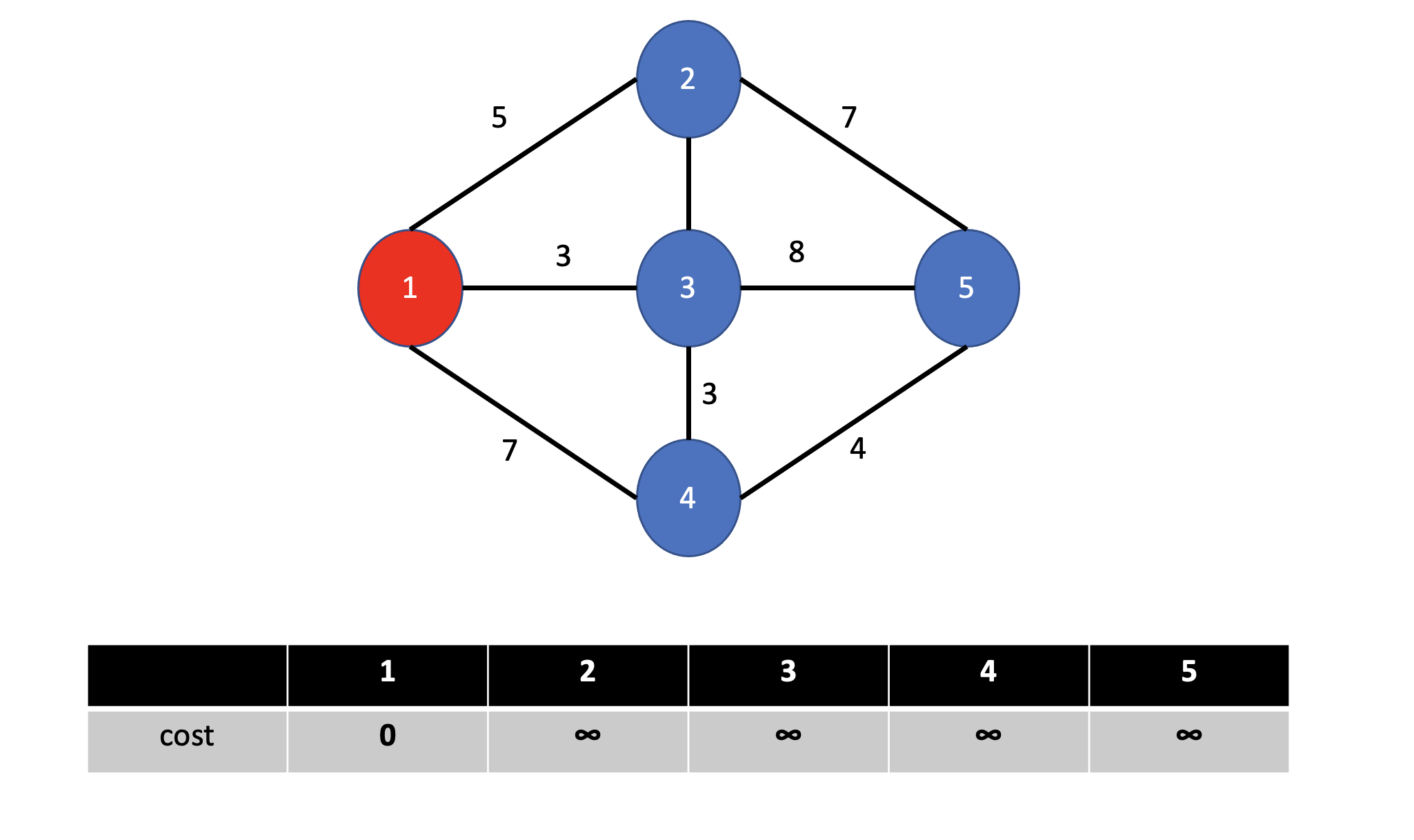
2. 아직 방문하지 않은 정점 중 거리가 가장 짧은 정점을 방문합니다.

  • 1 이겠지요?

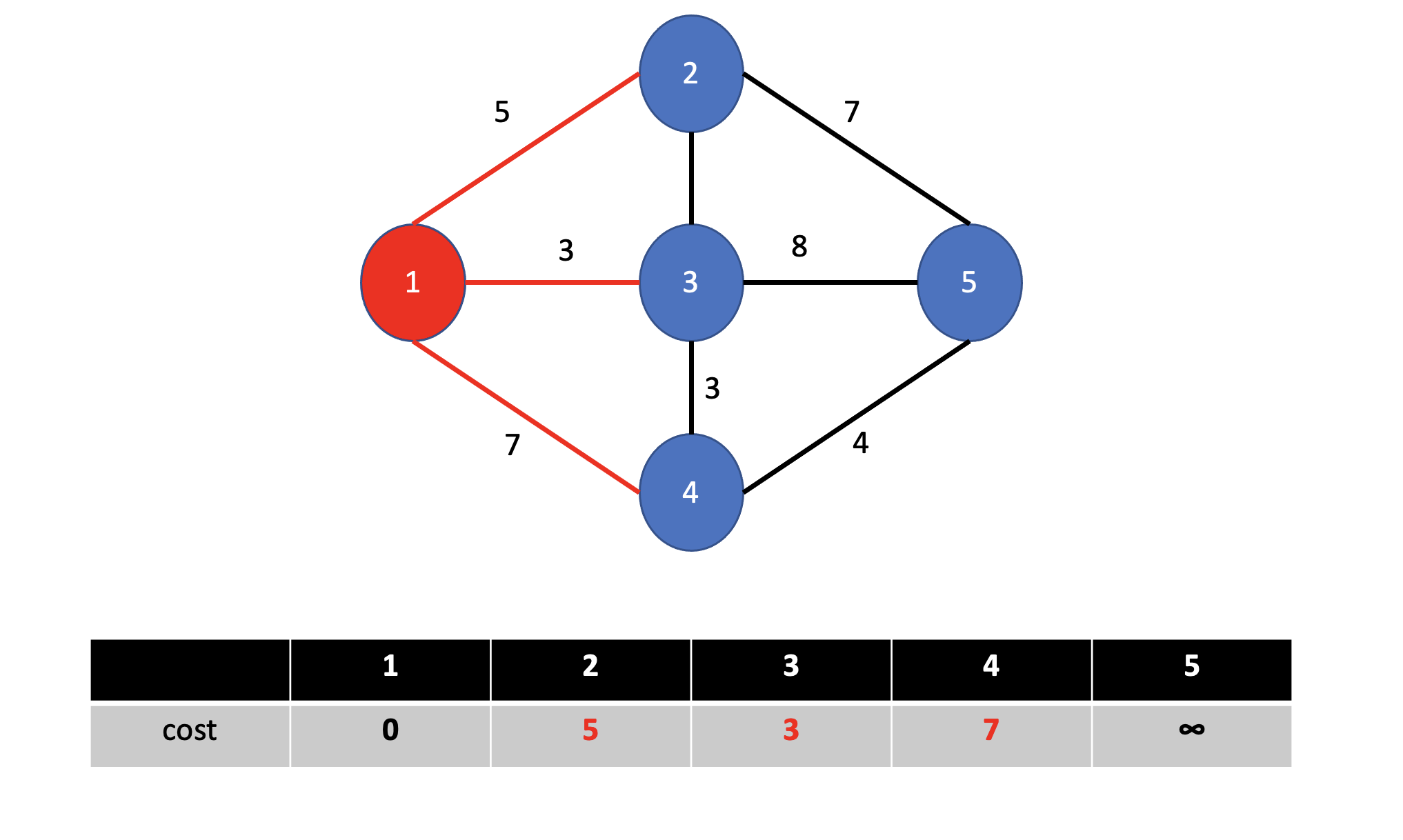
3. 해당 정점에서 인점하고, 아직 방문하지 않은 정점들의 거리를 갱신합니다.

  • 1번 정점에서 인접하고, 아직 방문하지 않은 정점들은 2,3,4 겠지요?

거리 갱신 방법은
1번 점정을 통해 K번 정점으로 가는 거리는 dist[1] + dist[1][k] (1~K 거리)이고,
만약 이 값이 dist[K] 보다 작다면, dist[K] 는 갱신됩니다.
현재 0번을 제외한 모든 정점의 값이 무한대이므로, 모두 갱신됩니다.

1번 방문 끝

그럼 이제 다시 2. 아직 방문하지 않은 정점 중 거리가 가장 짧은 정점을 하나 선택해 방문합니다.

  • 3번이 거리가 3으로 가장 짧으니, 3번을 방문해줍니다.

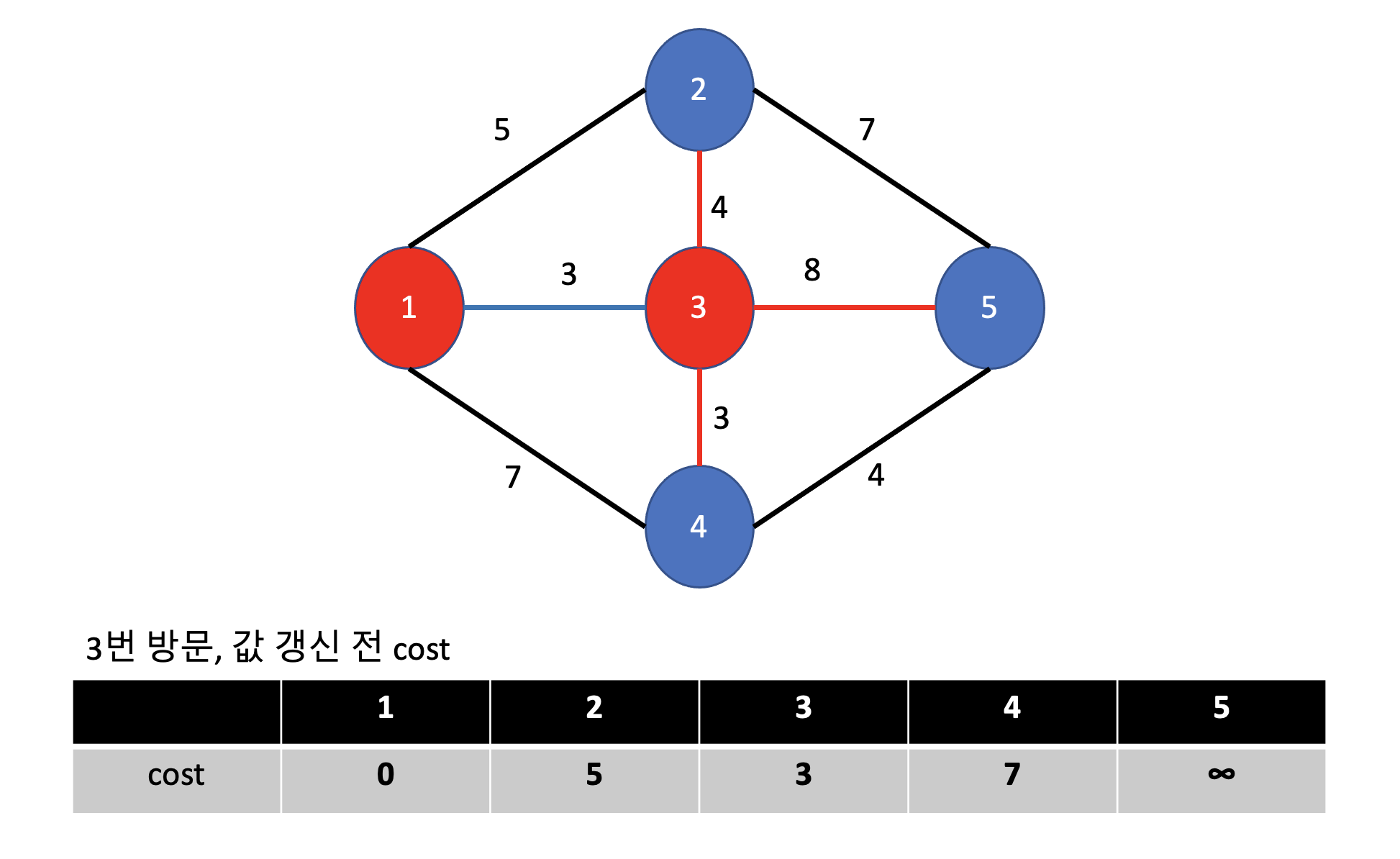
3. 해당 정점에서 인점하고, 아직 방문하지 않은 정점들의 거리를 갱신합니다.

  • 3번 정점에서 인접하고, 아직 방문하지 않은 2, 4, 5 정점을 살펴봅시다.

2번 정점의 거리

    1. dist[3] + dist[3][2] = 3번 정점값(3) + 3번에서 2번의 거리 (4)이므로 = 7
      ( 즉, 1->3->2 의 경로로 가는 거리입니다 )
    1. 현재 dist[2] 는 5 (1->2 의 거리입니다)

그렇다면 2번 정점은 갱신하면 거리가 더 길어지므로 갱신하지 않습니다.

4번 정점의 거리

    1. dist[3] + dist[3][4] = 3번 정점값(3) + 3번에서 4번의 거리 (3) 이므로 = 6
      (1->3->4 의 경로로 가는 거리 )
    1. 현재 dist[4] 는 7 (1-> 4의 경로)

그렇다면, 4번 정점은 갱신하면 거리가 더 짧아지므로, 6 으로 갱신합니다.

저희는 4번 정점이 1 -> 3 -> 4 의 경로로 갈 때,
3번 정점의 값을 가져왔고, 3번에서 4번으로 가는 경로만 더해주었지요?

💡 여기서 3번 정점 값을 가져와 계산한 부분
1 -> 3 의 과정을 생락하고, 3번 정점의 값으로 계산한 이 부분이 다이나믹 프로그래밍 기법, 메모이제이션을 활용한 부분이 됩니다.
하나의 최단 거리를 구할 때 그 이전까지 구했던 최단 거리 정보를 그대로 사용한다는 특징이 있습니다.

5번 정점의 거리

  • 현재 무한대이므로, dist[3] + dist[3][5] = 11 이 됩니다.

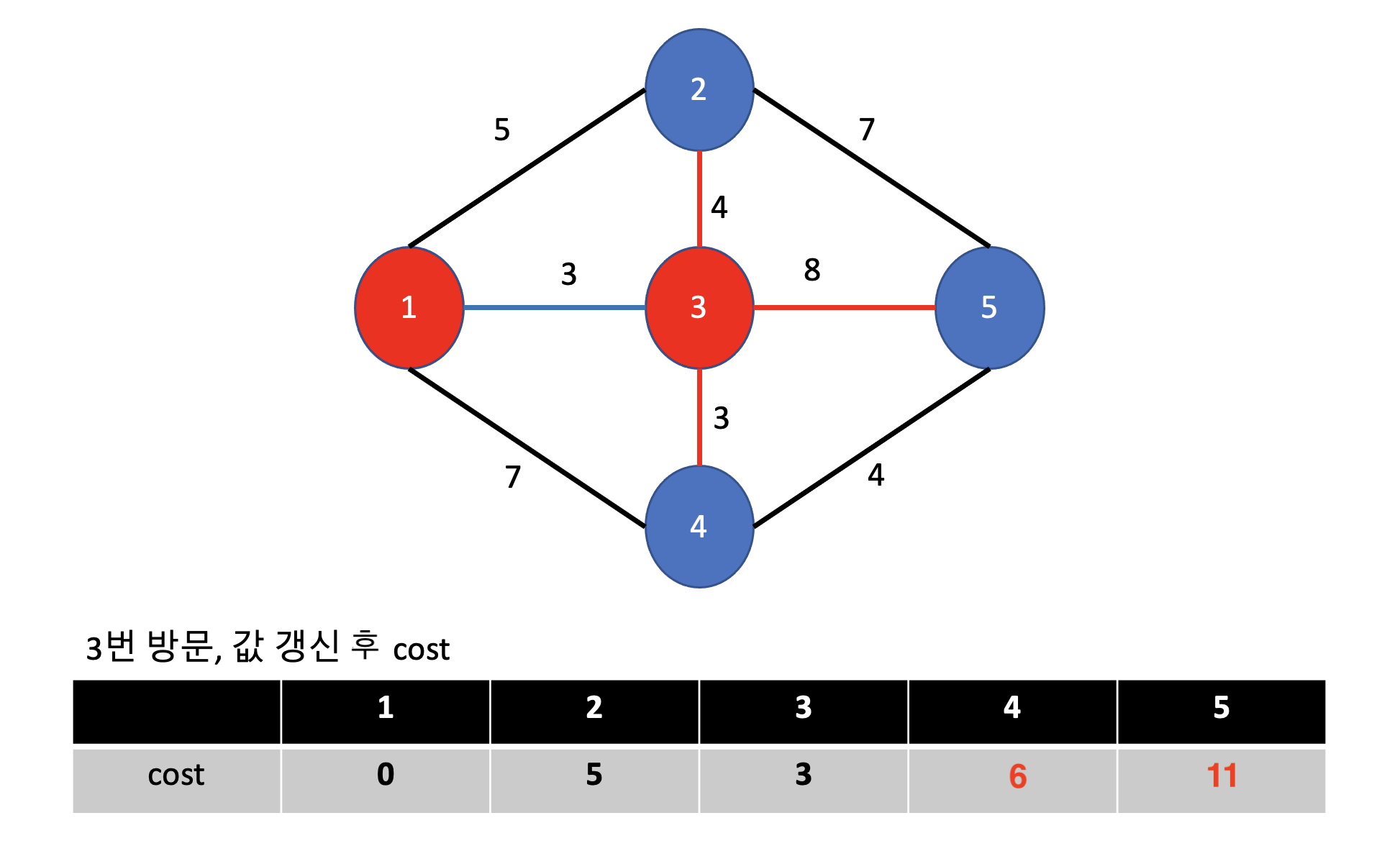
3번 방문 끝

그럼 다시, 2. 아직 방문하지 않은 정점 중 거리가 가장 짧은 정점을 하나 선택해 방문합니다.

  • 1,3 은 방문했고 2,4,5 중 2번이 거리가 가장 짧으므로 2번을 방문합니다.

3. 해당 정점에서 인점하고, 아직 방문하지 않은 정점들의 거리를 갱신합니다.

  • 2번 정점에서 인접하고, 아직 방문하지 않은 정점은 5 가 있네요.

5번 정점의 거리
이제 어떤 값을 구해야 하는 지 알겠죠?
1->2->5 의 경로를 계산하고, 현재 5번 값과 비교하면 됩니다.

  • dist[2] + dist[2][5] = 2번 정점값(5) + 2번에서 5번의 거리 (7) 이므로 = 12
    (1 -> 2-> 5 경로의 거리 )
  • 현재 dist[5] = 11

그렇다면 5 는 갱신하지 않고, 그대로 두겠네요.

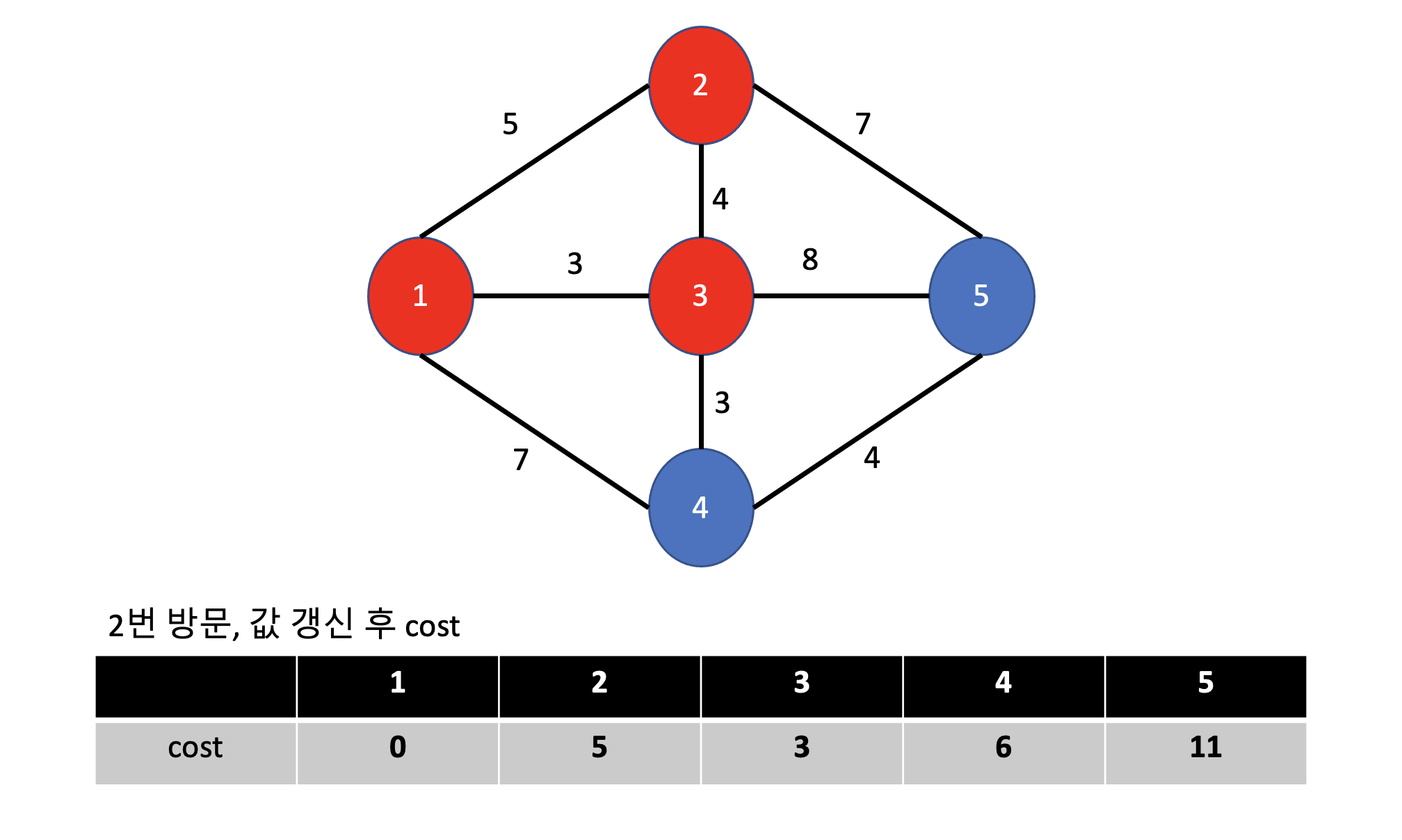
2번 방문 끝

다시, 2. 아직 방문하지 않은 정점 중 거리가 가장 짧은 정점을 하나 선택해 방문합니다.

  • 4번 정점이 가장 짧네요, 4번 정점을 선택하여 방문하겠습니다.

3. 해당 정점에서 인점하고, 아직 방문하지 않은 정점들의 거리를 갱신합니다.

  • 4번 정점에서 인접하고, 아직 방문하지 않은 정점은 또 5만 있네요.

이번에도 어떤 값을 구해야하는 지 알겠죠?
1 -> 4 -> 5 의 거리와, 현재 5번 값을 비교하면 됩니다.

5번 정점의 거리

  • dist[4] + dist[4][5] = 4번정점값(6) + 4번에서 5번의 거리 (4) = 10
    여기서 dist[4] = 1 -> 3 -> 4 의 거리였습니다,
    그럼 현재 10 은 1 -> 3 -> 4 -> 5 의 거리가 되겠죠?
  • dist[5] = 11
    이므로, 5번 정점은 10 으로 갱신되겠네요.

4번 방문 끝

마지막으로 5번 정점만 남았을 때는 나머지 정점을 다 방문한 상태이므로 아무것도 하지 않습니다.
끝 ! 이렇게 각 cost값이 1번 정점으로부터의 최단 거리가 되었습니다.

저희는 위와 같은 과정을 거치면서
1 -> 3 -> 5 의 과정도 계산하고
1 -> 2 -> 5 의 과정도 계산하고
1 -> 4 -> 5 의 과정을 계산하면서
1 -> 3 -> 4 -> 5의 과정도 하였습니다.
이렇게 최단 거리를 탐색하는 알고리즘 입니다.

코드 구현 (java)

그럼 이제 동작 방식을 알았으니, 구현을 해보도록 합시다.
아직 방문하지 않은 정점들 중에서 dist 값이 제일 작은 정점을 찾아 방문하는 부분이 문제인데요,
dist 값들을 다 비교해서 찾는 경우는 매번 O(V)고,
루프는 V-1번 실행되니까 O(V^2)의 시간복잡도가 발생하여 너무 큽니다.
그래서 저희는 여기에 우선순위 큐 를 적용합니다!

	public static void dijkstra(int startNode){
		// 최단 거리 정점을 가져와야하므로, 우선순위큐 사용
		PriorityQueue<Node> pq = new PriorityQueue<>(((o1, o2) -> Integer.compare(o1.cost, o2.cost)));
		pq.offer(new Node(startNode,0)); // 시작 노드 삽입

		while(!pq.isEmpty()){
			Node now = pq.poll(); // 현재 정점
			for(Node nxt : graph[now.idx]){ // 인접한 정점들
				int nextNode = nxt.idx;
				if(dist[nextNode] < now.cost ) continue ; // 현재 정점의 거리보다 다음 정점의 거리가 짧은 경우 확인할 필요X, 리턴
				if(dist[nextNode] > now.cost + nxt.cost){ // 인접한 정점의 거리가, 현재 정점 거리 + 다음 정점 거리보다 클 때
					dist[nextNode] = now.cost + nxt.cost; // 값을 갱신해주고
					pq.offer(new Node(nextNode, dist[nextNode])); // Q 에 삽입
				}
			}
		}	
	}

끝! 쉽죠?

다익스트라를 적용한 가장 기초적인 백준 문제로 코드를 적용해보겠습니다.
백준 - 최단 경로

import java.util.*;
import java.io.*;

class Node{
	int idx;
	int cost;
	Node(int idx, int cost){
		this.idx = idx;
		this.cost = cost;
	}
}

public class Main{

	static int V, E ; // V : 정점의 개수, E : 간선의 개수
	static int startNode ; // 시작 노드
	static ArrayList<Node>[] graph ; // 그래프 정보
	static int[] dist ;

	public static void main(String args[]) throws Exception{
        // 값 입력받기 --> 
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		StringTokenizer st = new StringTokenizer(br.readLine());
		V = Integer.parseInt(st.nextToken());
		E = Integer.parseInt(st.nextToken());

		startNode = Integer.parseInt(br.readLine());

		graph = new ArrayList[V+1];
		dist = new int[V+1];
		for(int i=0;i<V+1;i++){
			graph[i] = new ArrayList<>(); // 그래프 초기화
			dist[i] = Integer.MAX_VALUE; // 초기값 무한대
		}

		for(int i=0;i<E;i++){
			st = new StringTokenizer(br.readLine());
			int u = Integer.parseInt(st.nextToken());
			int v = Integer.parseInt(st.nextToken());
			int w = Integer.parseInt(st.nextToken());
			
			graph[u].add(new Node(v,w));
		}
		// <--

		dist[startNode] = 0 ; // 시작노드 = 0
		dijkstra(startNode);
		
		for(int i=1;i<V+1;i++){
			if(dist[i] == Integer.MAX_VALUE) System.out.println("INF");
			else System.out.println(dist[i]);
		}
	}
	
	public static void dijkstra(int startNode){
		// 최단 거리 정점을 가져와야하므로, 우선순위큐 사용
		PriorityQueue<Node> pq = new PriorityQueue<>(((o1, o2) -> Integer.compare(o1.cost, o2.cost)));
		pq.offer(new Node(startNode,0));
		while(!pq.isEmpty()){
			Node now = pq.poll(); // 현재 정점
			for(Node nxt : graph[now.idx]){ // 인접한 정점
				int nextNode = nxt.idx;
                if(dist[nextNode] < now.cost ) continue ; // 현재 정점의 거리보다, 다음 정점의 거리가 짧은 경우 확인할 필요X, 리턴
				if(dist[nextNode] > now.cost + nxt.cost){ // 인접한 정점의 거리가, 현재 정점 거리 + 다음 정점 거리보다 클 때
					dist[nextNode] = now.cost + nxt.cost; // 값을 갱신해주고
					pq.offer(new Node(nextNode, dist[nextNode])); // Q 에 삽입
				}
			}
		}	
	}

}

3. 시간 복잡도

인접 리스트를 사용하고, 우선순위큐를 사용하였을 경우
정점 개수가 V, 간선 개수가 E일 때 O(ElogV)의 시간복잡도를 갖습니다.

인접행렬로 구현했다면 매번 인접한 정점을 찾아야 하니
루프마다 O(V)의 시간이 소요되어서 총합 O(V^2)가 될 것입니다.

관련 문제

(문제들은 밑에 참고 게시글 블로그에서 가져온 리스트입니다! 제가 편하게 보려고 문제만 리스트업해둔 것이니,
문제마다 설명은 아래 rise 슈퍼마리오님의 블로그를 참고하시면 아주 도움이 될 것 같습니다 :-) )

참고
안경잡이 개발자 blog - 다익스트라 알고리즘
Rise 마법의 슈퍼마리오 blog - 다익스트라 알고리즘

profile
ideal dev
이전 포스트

[알고리즘] 백트래킹 기법

0개의 댓글