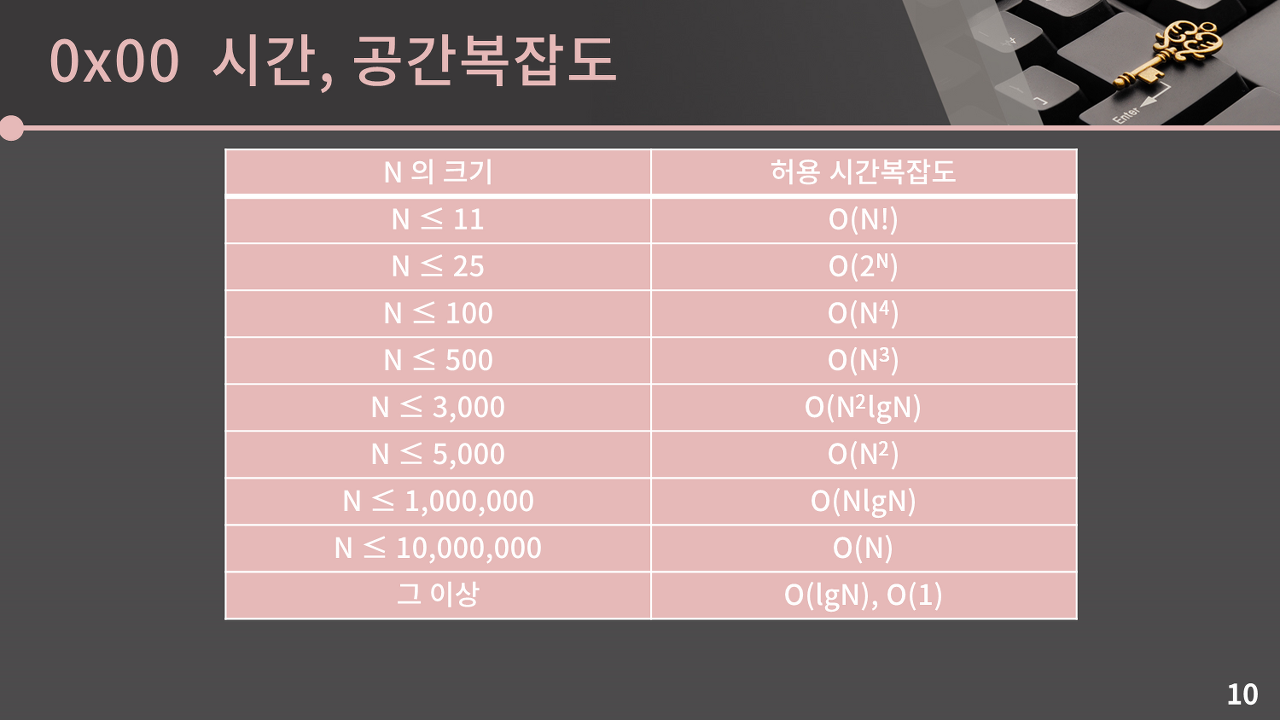
시간복잡도

예시
N명의 사람들이 일렬로 서 있을 때, 이름이 가나다인 사람을 찾는 데 걸리는 시간은?
N번 확인해야하므로, 시간복잡도는 O(N)
N명의 사람들이 이름순으로 서 있을 때, 이름이 가나다인 사람을 찾는 데 걸리는 시간은?
중간 값을 확인하며 범위를 줄여나갈 수 있으므로(이분탐색), 시간복잡도는 O(logN)
문제에서 주어지는 시간복잡도는 1~5초 사이이므로 확인하고 시간초과가 나지 않도록 코드 생각하기!
코드 예제
N이하의 자연수 중 3의 배수 또는 5의 배수를 모두 합한 값을 반환하는 함수 func(arr[],int N)를 작성하여라. N은 5만 이하의 자연수이다.
int func(arr[],int N){
int sum = 0;
for(int i=1; i<=N; i++){
if(i%3 == 0 || i%5 == 0) sum+=i;
}
return sum;
}=> 단순히 1부터 N까지 확인하며 3또는 5의 배수인지 확인하는 방법. 시간복잡도는 O(N)
길이 N의 정수형 배열 arr에서 합이 100인 서로 다른 위치의 두 원소가 존재하면 1을 반환, 존재하지 않으면 0을 반환하는 함수 func2 (arr[],int N)를 작성하여라. arr의 각 수는 0이상 100이하, N은 1000이하이다.
int func2(arr[],int N){
for(int i=0; i<N; i++){
for(int j=i+1; j<N; j++){
if(arr[i]+arr[j] == 100) return 1;
}
}
return 0;
}=> 역시 하나하나 단순 비교, 시간복잡도 O(N^2)의 방법. O(N)의 효율적인 방법이 있지만 여기서는 일단 패스
N이 제곱수이면 1을, 제곱수가 아니라면 0을 반환하는 함수 func3(int N)를 작성하여라. N은 10억이하의 자연수이다.
int func3(int N){
for(int i=1; i*i<=N; i++){
if(i*i == N) return 1;
}
return 0;
}=> i값이 1부터 i의 제곱수가 N이하일 때까지 반복하며 찾기. 시간복잡도는 O(√N). 시간복잡도 내부에는 루트도 가능!
이 부분 코드 짤 때 반복문 경계값을 그냥 N/2로 하면 되나.. 하고 생각했었다 처음에ㅠ 바보
N이하의 자연수 중에서 가장 큰 2의 거듭제곱수를 반환하는 함수 func4(int N)을 작성하여라. N은 10억이하의 자연수이다.
int func4(int N){
int result = 1;
while(val <= N){
result *= 2;
}
return result;
}=> while문을 이용한 방법. N이 16일때 4번, N이 1024일때 10번 실행된다. N이 2^k일 때는 k번 실행되므로 로그의 정의에 입각하여 시간복잡도는 O(logN).
공간복잡도
공간복잡도는 코딩테스트에서 크게 중요하지 않긴 함,,, 대신 메모리 제한 체크
메모리 제한 512MB = 1.2억개의 int까지 가능
=> 크기 5억의 배열이 사용되는 코드는 불가능!
정수 자료형
char / short / int / long long

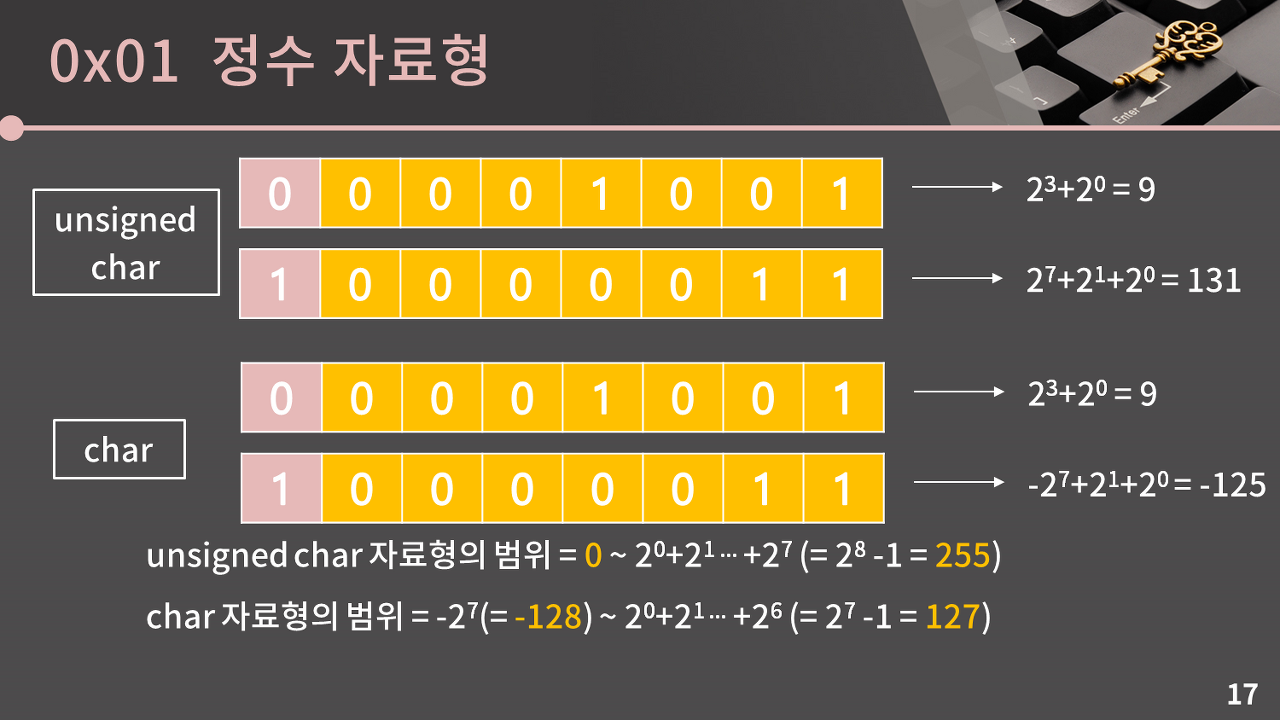
1바이트는 8비트이므로, char형은 0또는 1이 8개의 칸에 들어가서 표현된다

int형의 최대값은 대략 21억!
Integer Overflow?
간단히 말하여 char형 자료형의 최대값이 127에 1을 더한다면?
128이 아닌 -128이 되는 경우.

세 함수 중 오버플로우가 나는 경우는 왼쪽 상단과 오른쪽 함수이다.
왼쪽 상단 함수 func1의 경우, s = 127에서 s++가 될때 -128이 되며 무한루프에 진입한다.
오른쪽 함수 func3의 경우, a = 10^9일때 10이 곱해지면서 int형 범위를 벗어나 오버플로우 발생. 이 경우 a의 자료형을 long long으로 바꾸거나, 7번째 줄의 10 -> 10ll 또는 (long long)10으로 바꾸어 해결할 수 있음.
실수자료형
float/double


컴퓨터가 실수를 저장하는 방법을 알기 위해서는 우선 이진수로 실수를 나타내는 법에 대해 알아보자.
실수를 이진수로 나타내는 방법은 위와 같다. 이때 이진수에서도 무한소수가 존재하는데, 1/3과 같은 수는 이진수로는 무한소수로 나타난다.

IEEE-754 format - 실수 저장 방식
이진수에서도 편의상 유효숫자 표기법처럼 표기할 수 있다.
실수를 나타낼 때 칸은 sign/exponent/fraction의 세 가지 필드로 나누어진다.
sign칸은 부호를, exponent는 과학적 표기법의 지수를, fraction은 유효숫자를 저장하는 필드이다.
각 필드의 크기는 float형에서는 1 / 8 / 23 bit , double형에서는 1 / 11 / 52 bit 이다.
예를 들어, -6.75는 이진수로 표기했을 때 -1.1011x2^2이다.
sign 필드를 보면, 음수이므로 1이 입력된다.
exponent 필드를 보면, 2의 지수가 2이고 여기에 127을 더한 값은 129이므로 129의 이진수인 10000001이 입력된다. (127을 더하는 이유는 음수인 지수도 입력하기 위해서)
fraction 필드를 보면, 가장 앞의 1을 제외하고 1011이 해당한다. 맨 왼쪽부터 2^-1, 2^-2자리인 셈이라 1011000....00 이 입력된다.
참고하기 https://blog.naver.com/xtelite/50016744276
알아야 하는 이유 -> 실수의 성질

놀랍게도 0.1+0.1+0.1이 0.3이 아니랍니다!
원인은 유효숫자가 들어가는 fraction 필드가 유한하기 때문. float은 앞의 23비트, double은 52비트까지만 잘라서 저장할 수 있다.
0.1은 이진수로 표현하면 무한소수가 되어 오차가 발생한 채로 저장되는데, 그 상태로 세 번이 저장되어 더 커진 오차로 인해 0.3과 다른 값으로 인식이 된 경우이다.
float형의 경우 유효숫자가 6자리이므로 상대오차 10^-6까지 안전하고, double형의 경우 유효숫자가 15자리이므로 상대오차 10^-15까지 안전하다.
-> 그냥 앵간하면 float대신 double형 쓰자

double의 유효숫자는 15자리, long long의 유효숫자는 19자리이다.
사진과 같이 double형에서는 10^18과 10^18+1을 구분하지 못함...! 하지만 int형은 최대 21억이기때문에 double형에 담아도 ㄱㅊ

위에서 보았듯 오차때문에 등호를 사용하여 비교하면 안된다. 대신 두 값의 차이가 10^-12(대략적인 아주 작은 값)이하이면 같다고 보면 된다.
출처 - 바킹독의 실전 알고리즘
