
알고리즘 설명

재귀는 하나의 함수에서 자기 자신을 다시 호출해 작업을 수행하는 알고리즘.
위 이미지에서는 재귀를 이용하여 N부터 1까지 출력하는 함수와 1부터 N까지의 합을 구하는 함수를 보여준다.
이 코드가 올바르게 작동하는 원리를 알아보자.
재귀로 푼다는 것 → 귀납적 방식을 이용한다.
귀납적 방식이란?

위 사진에서, 제일 앞의 도미노를 쓰러트리게 되면 모든 도미노가 쓰러질 것이다. 상식적으로 생각해보면 1번 도미노가 쓰러지면 2번 도미노가 쓰러지고, 2번 도미노가 쓰러지면 3번 도미노가 쓰러지고, 3번 도미노가 쓰러지면 4번 도미노가 쓰러지고…. 이런 식으로 계속 진행되기 때문에 모든 도미노가 쓰러진다는 것을 알 수 있다.
반면 수학적 귀납법을 이용하여 설명해보자면,
1번 도미노가 쓰러진다.
k번 도미노가 쓰러지면 k+1번 도미노도 쓰러진다.
이 두가지 명제가 참이기 때문에 모든 도미노가 쓰러진다는 결론이 나온다. 결국 수학적 귀납법도 풀어서 보면 1번 도미노가 쓰러지고, 이후에 2번 도미노가 쓰러지고… 이렇게 연쇄적으로 진행이 되어 모든 도미노가 쓰러지기 때문에 참이 된다. 하지만 앞으로는 두 명제가 참인 것까지만 생각한 후 바로 결론에 도달할 수 있어야 한다.
우리는 지금까지 순차적으로 명령을 내리고, 조건을 확인하고 실행하는 절차 지향적인 방식으로 코드를 진행해왔다. 이런 사고방식을 탈피해보자!
절차지향적 사고 vs 귀납적 사고
n부터 1까지 출력하는 함수 func1을 두 가지 방식으로 생각해보자.
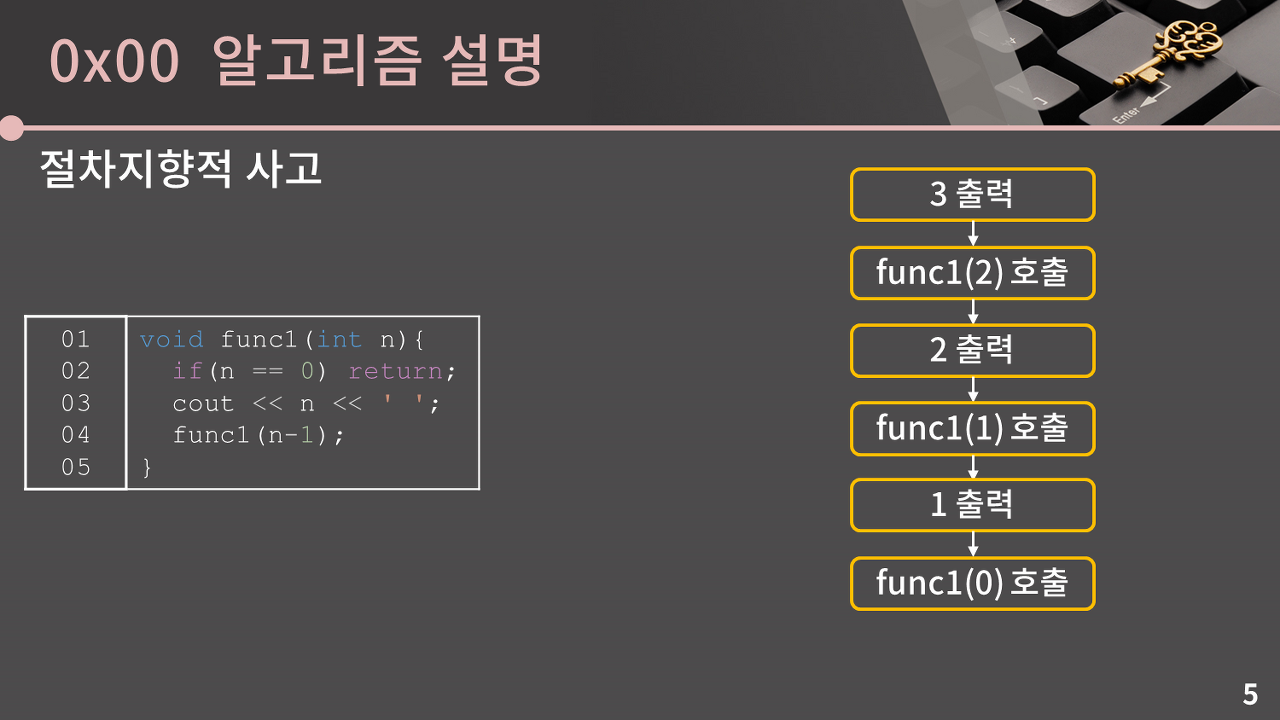
절차 지향적 사고는 일반적으로 우리가 생각하는 방식이다. func1(3)의 결과를 예상해보면, 오른쪽의 순서로 순차적으로 진행하며 3 2 1 이 출력될 것임을 알 수 있다.

이번에는 귀납적 사고를 이용하여 func1 함수가 n부터 1까지 차례로 출력하는 함수임을 이해하는 방식이다.
첫 번째로 func1(1)이 1을 출력한다는 자명한 명제가 있다.
그 다음 우리는 func1(k)가 k k-1 k-2 … 1을 출력하면, 즉 k부터 1까지 차례대로 출력하면 func1(k+1)은 k+1부터 1까지 차례로 출력한다는걸 증명해야 한다.
이를 증명하기 위해서는 "func1(k)는 k부터 1까지 차례로 출력한다" 는 가정을 설정한 후, func1(k+1)이 호출될 때의 상황을 살펴보면 된다.
func1(k+1)이 호출되면, k+1이 출력된 이후 func1(k)가 호출된다. func1(k)는 k부터 1까지 차례로 출력하기 때문에 func1(k+1)은 k+1부터 1까지 차례대로 출력함을 증명할 수 있다.
func1(1)이 1을 출력한다. (자명한 명제)
func1(k)가 k부터 1까지 차례로 출력한다. (가정)
→ func1(k+1)은 k+1부터 1까지 차례로 출력한다. (결론)
재귀함수의 조건

1. 재귀 함수는 반드시 특정 입력(base condition)에 대해서는 자기 자신을 호출하지 않고 종료되어야 한다.
2. 모든 입력은 base condition으로 수렴해야 한다.
위 코드에서 n = 0일 때 return이 되므로, base condition은 n=0이다.또한 이 함수는 자연수만 입력되기 때문에 모든 입력은 결국엔 n = 0으로 수렴하게 된다.
두 조건을 모두 만족시키므로 func1은 올바르게 동작하게 된다.
이 두 조건 중 어느 하나라도 지켜지지 않는다면 재귀 함수는 결과를 내지 못하고 무한히 들어가다가 런타임 에러가 발생하게 된다.
재귀함수 사용 팁

먼저 재귀에서는 함수를 명확하게 정의해야 한다. 정의라는건 함수의 인자로 어떤 것을 받을지, 그리고 어디까지 계산한 후 자기 자신에게 넘겨줄지를 의미한다. 함수의 형태를 잡는 부분을 많이 연습해보자.
그리고 모든 재귀 함수는 재귀 구조 없이 반복문만으로 동일한 동작을 하는 함수를 만들 수 있다. 재귀는 적재적소에 사용하면 코드가 간결해지지만 함수 호출이 꽤 비용이 큰 연산이기 때문에 메모리와 시간에서는 손해를 볼 수 있다. 그렇기 때문에 굳이 재귀를 쓰지 않아도 구현에 큰 어려움이 없으면 재귀 대신 반복문으로 코드를 짜는게 좋지만, 재귀 없이 구현을 하면 코드가 너무 복잡해지는 일부 문제들은 재귀로 구현을 하는게 좋다.

재귀 함수가 자기 자신을 여러 번 호출하게 되면 비효율적일 수 있다.
위의 fibo 함수는 n번째 피보나치 수열을 반환하는 함수이다. 조건을 살펴보면 base condition은 n <= 1 이고, 모든 입력에 대해 base condition으로 수렴할 것이므로 재귀함수의 두 조건을 만족한다.
n번째 피보나치 항을 구하기 위해 필요한 연산의 횟수를 생각해보면 상식적으로 생각했을 때 앞에서부터 차례로 1 1 2 3 5 8… 이렇게 가면 n번의 덧셈이 필요하다. 즉 O(n)이라고 생각할 수 있다.
하지만 fibo함수의 시간복잡도는 놀랍게도 O(1.618n)이다.
이런 일이 발생한 이유는 무엇일까? 함수의 호출을 되짚어보자.
fibo(5)가 호출된 상황을 예로 들어보자.
fibo(5)는 fibo(4)와 fibo(3)을 호출한다.
fibo(4)는 fibo(3)과 fibo(2)을 호출한다.
fibo(3)은 fibo(2)와 fibo(1)을 호출한다.
전체적인 재귀 호출 상황을 나타내보면 오른쪽 그림과 같다. 그림을 보면 이미 계산한 값을 또 계산한다는 일이 계속 발생하고, 시간복잡도도 이에 따라 더 커진 것을 알 수 있다. 이처럼 한 함수가 자기 자신을 여러 번 호출할 경우에는 시간복잡도가 불필요하게 커질 수 있다. 위의 피보나치 문제는 재귀 대신 나중에 배울 다이나믹 프로그래밍을 이용해 O(n)에 해결할 수 있다.

재귀 함수가 자기 자신을 부를 때 스택메모리에 함수에 대한 정보가 누적된다.
재귀가 깊게 들어가는 풀이라면, 이 영역에 제한된 메모리 이상을 사용하게 되고, 런타임 에러가 발생하게 된다. 이 경우, 재귀 대신 다른 방법을 이용해야한다.
참고로 스택 메모리에는 지역 변수도 들어가기 때문에, 이러한 메모리 제한을 초과한 에러가 발생한 경우 재귀의 문제가 아니라면 지역 변수로 int arr[2000][2000]과 같은 큰 배열을 잡았을 경우가 있다. (int 400만개면 16MB에 해당한다)
연습문제 - 거듭제곱

a^b 를 m으로 나눈 나머지, 즉 a^b mod m을 구하려면? 쉽게 떠오르는 방법은 a를 b번 곱한 뒤 m으로 나누는 방법이다. 코드는 위와 같고, 만약 func1(6, 100, 5)를 넣으면 6^100 mod 5의 결과인 1 출력된다고 추측할 수 있다. 하지만 결과는 놀랍게도 1이 아니라 0이 출력된다.
코드가 제대로 작동하지 않는 이유는?

그 이유는 바로 6^100은 int의 범위를 벗어나 발생한 int overflow 때문! 이를 해결하기 위해 곱하는 과정 중 값을 m으로 나눠서 나머지만 생각하면 된다. 그리고 type도 long long으로 바꿔주는 편이 더 좋다. 아래 코드를 보면 m 미만의 수 2개를 곱하는 상황이 계속 발생하니 m이 2^32 보다 크다면 long long의 범위조차 넘어설 수 있지만, 코딩 테스트에서는 그럴 일은 거의 없음. 결론적으로 a^b mod m을 O(b)에 구할 수 있다.
b가 최대 20억이라서 O(b)로는 해결할 수 없을 때는? a를 b번 곱하는 방식은 분명 시간 초과가 발생할 것이다. 아래 문제를 풀어보자.
BOJ 1629 곱셈

힌트는 위와 같다.
13을 5으로 나눈 나머지는 3이고, 169를 3으로 나눈 나머지는 9이다.
12^58을 67로 나눈 나머지가 4라는 것을 알고 있으면, 12^116을 67로 나눈 나머지는 4^2=16임을 알 수 있다.
이를 귀납적으로 해결하려면?
1승을 계산할 수 있다.
k승을 계산할 수 있다면, 2k승과 2k+1승을 계산할 수 있다.
#include <iostream>
using namespace std;
long long a,b,m;
long long POW(long long a,long long b,long long m){
if(b == 1) return a % m;
//
long long val = POW(a,b/2,m);
val = val * val % m;
if(b % 2 == 0) return val;
else return val * a % m;
}
int main()
{
cin >> a >> b >> m;
cout << POW(a,b,m);
return 0;
}연습문제 - 하노이 탑
BOJ 11729 하노이 탑 이동 순서


