62. Unique Paths

문제 설명

MxN 격자에 로봇이 있다. 이 로봇은 가장 왼쪽 위(grid[0][0])에 위치해 있다. 로봇은 가장 오른쪽 아래(grid[m-1][n-1])로 가려고 한다. 한번에 아래 또는 오른쪽으로만 움직일 수 있다.
m,n이 주어질 때, 로봇이 도달할 수 있는 가능한 경로의 가짓수를 출력하시오. 정답은 2*10^9 이하이다.

출력 예시

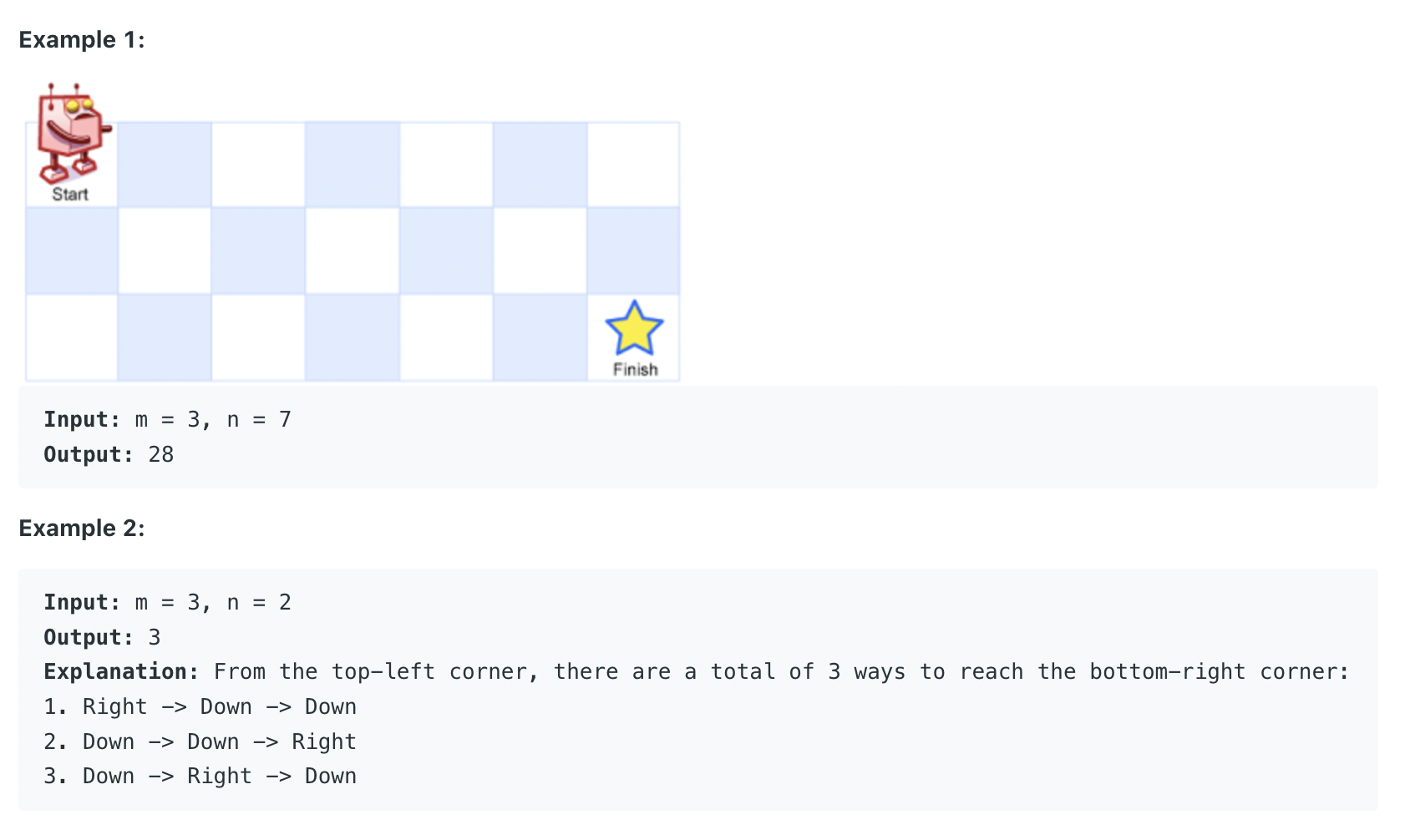
접근 방법

첫번째 시도

최단 경로가 아니라~ 경로에 관계없이 아래로 x번, 오른쪽으로 y번 이동함은 항상 동일함. 즉 전체 가짓수는 (x+y)!/x!y! (문제의 경우 x = n-1, y = m-1)
= > Combination 코드로 구현하기
이차원 배열과 큐를 이용해 이전 값들을 담으려다가 계속 시간초과,,

두번째 시도

맞는 방법인지는 모르겠으나 조합을 풀어쓴 식
{a/(bc)}{(a-1)/(b-1)(c-1)}* ....
의 형태로 반복문을 돌림.
한번에 분자 분모를 계산해서 나눠버리면 값이 너무 커지기 때문에 중괄호 하나를 한번에 반복했다.

소스코드

class Solution {
public:
    int uniquePaths(int m, int n) {
        long long result[101][101]={0};
        if(m==1 || n==1) return 1;
        else{
            double answer=1.0;
            double small_num=min(m,n)-1;
            double large_num=max(m,n)-1;
            double sum_num=small_num+large_num;
            while(sum_num > 1){
               answer *= (sum_num)/((small_num)*(large_num)); 
                if(small_num > 1) small_num--;
                if(large_num > 1) large_num--;
                sum_num--;
            }
            
            return round(answer);
        }
    }
};

돌아보기

반복문 아래처럼 줄일 수 있다... 똑똑한 사람들..

        for(int i=1 ;i<=small_num;i++){
            answer *= (sum_num-small_num+i)/i;
        }