• 문제 링크 : 14501번: 퇴사

문제 파악

• 퇴사하기 전, N일 동안 최대한 많은 상담을 하려고 한다.
• 입력
  • N : 상담일 수 (1 ≤ N ≤ 15)
  • Ti, Pi : 상담을 완료하는데 걸리는 기간, 상담을 했을 때 받을 수 있는 금액 (1 ≤ Ti ≤ 5, 1 ≤ Pi ≤ 1,000)
• 출력
  • 얻을 수 있는 최대 수익

코드 설계 및 구현

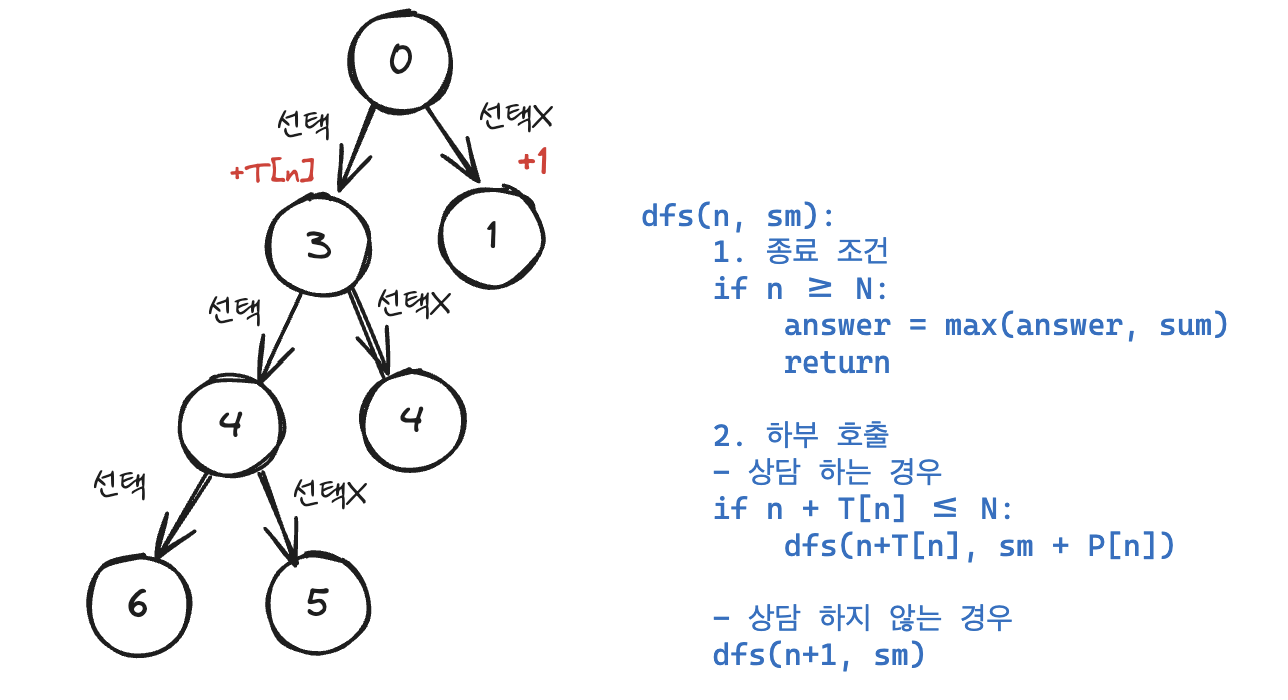
풀이 1 - 완전탐색

• 상담일 수가 최대 15일이므로 완전 탐색으로도 구현 가능
• 가능한 모든 경우를 트리로 표현 가능
• 상담 하는 경우에는 날짜에 T[n] 을 더하고, 상담하지 않는 경우는 날짜에 1을 더한다.
• 종료 조건 : 날짜 == N
  • 종료조건에 도달하면 정답을 최댓값으로 갱신한다.

N = int(input())

T = [0]*N
P = [0]*N

for i in range(N):
    T[i], P[i] = map(int, input().split())
    
def dfs(n, sm):
    global answer
    # 종료 조건
    if n >= N:
        answer = max(answer, sm)
        return
    # 하부 호출
    # 상담하는 경우(퇴사일 전 완료할 경우만 가능)
    if n + T[n] <= N:
        dfs(n+T[n], sm+P[n])
    # 상담하는 경우 (항상 가능)
    dfs(n+1, sm)

answer = 0
dfs(0, 0)
print(answer)

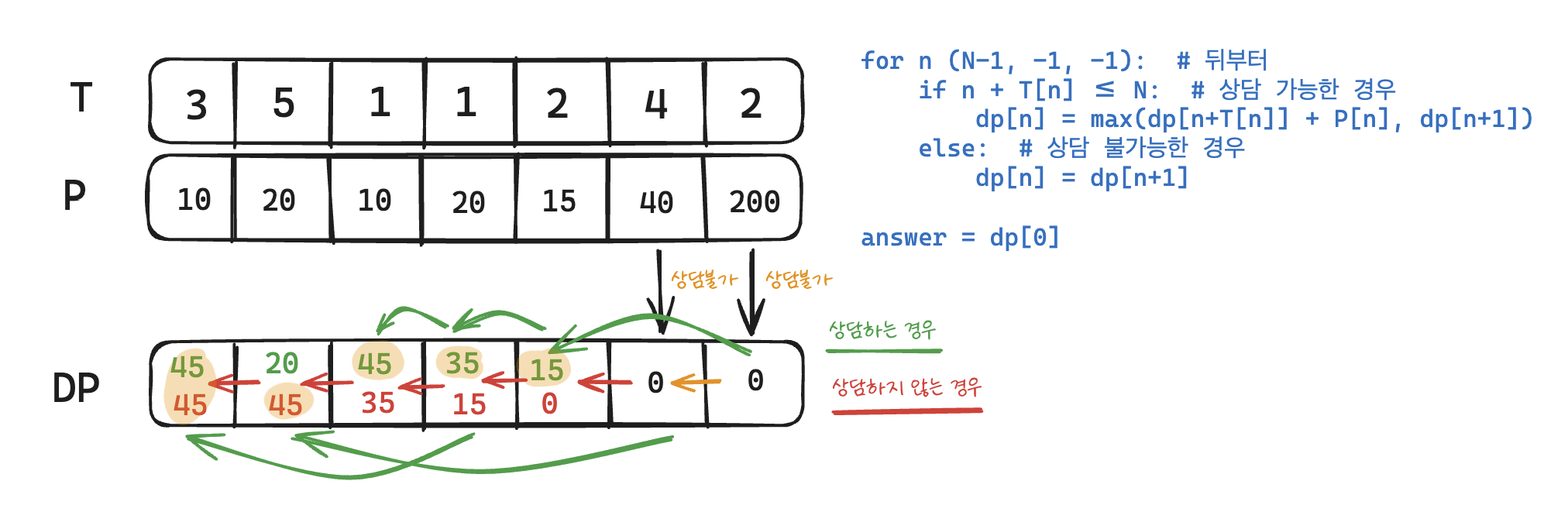
풀이 2 - DP

• 마지막 인덱스부터 확인하며 최대 수익 갱신
• dp[i] : i 번째 상담 결정 시 최대 수익
  • dp[n+1] : 상담 하지 않았을 때
  • dp[n+T[n]] + P[n] : 상담 했을 때

N = int(input())

T = [0]*N
P = [0]*N
for i in range(N):
    T[i], P[i] = map(int, input().split())

DP = [0]*(N+1)

for i in range(N-1, -1, -1):  # 뒤에서 앞으로
    if i + T[i] <= N:  # 기간 내 상담 완료 가능한 경우
        DP[i] = max(DP[i+T[i]]+P[i], DP[i+1])  # 상담 선택한 경우와 상담 선택하지 않은 경우의 최대 수익
    else:
        DP[i] = DP[i+1]

print(DP[0])

제출 결과

References

• [삼성 기출 #01] 14501. 퇴사 (백준, 파이썬)