Pre-course 7

7일차

딥러닝 학습방법 이해하기

• 신경망을 수식으로 분해
  • 신경망: 비선형모델. 선형모델과 활성함수(activation function)를 합성한 함수
  • X(nxd): 입력 데이터 행렬, W(dxp): 가중치 행렬(데이터를 다른 공간으로 보냄), b(nxp): y절편(각 행들이 모두 같은 값)
  • O(nxp) = XW+b
  • 출력 벡터 차원은 d에서 p로 변화
• 소프트맥스 연산
  • 모델의 출력을 확률로 해석할 수 있게 변환해주는 연산. 분류
  • softmax(o) = softmax(Wx+b)
    
  • 추론시: 원-핫 벡터(최대값 가진 주소만 1로 출력하는 연산) 하므로 소프트맥스 사용 x
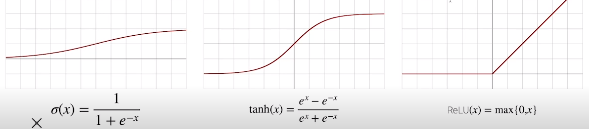
• 활성함수: 비선형 함수. ReLU 함수 주로 사용 (과거에는 sigmoid, tanh 함수)
  
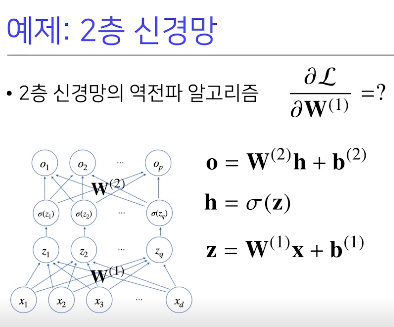
  • 다층퍼셉트론(Multi-Layer Perceptron): 신경망이 여러층 합성된 함수
  • H = 시그마(Z)
  • 순차적인 신경망 계산: 순전파(forward propagation)
  • 층이 갚을 수록 목적함수 근사하는데 필요한 뉴런(노드) 숫자가 빨리 줄어들어 효율적으로 학습 가능
• 역전파 알고리즘 backpropagation: 각 층에 사용된 파라미터 학습. 위층에서 아래층으로. 역순으로 계산
  • 합성함수 미분법인 연쇄법칙 기반 자동 미분
  • 미분값 저장해야하므로 메모리 많이 필요
    
    

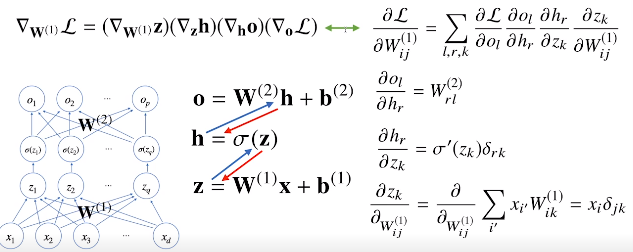
뉴럴 네트워크 - MLP

• 선형회귀: 입력 - 출력 파라미터 찾기
  • y = wx + b 에서 w, b 찾기
  • 로스가 줄어드는 방향으로 파라미터 변경: 로스/w 미분해서 역수 방향으로. loss 를 w, b에 대해 편미분, 작아지는 방향으로 반복 계산, 업데이트
  • y = W^T x + b
  • 내부에 여러 층을 쌓음: 행렬의 곱으로 표현 ( 한 층이랑 비슷함 - 선형이므로 )
    -> nonlinear transform 필요
  • Rectified Linear(ReLU), Sigmoid, Hyperbolic Tangent
  • loss function: Regression Task, Classification Task, Probabilistic Task

선형변환

• Transformation
  • Domain: 정의역 x
  • Co-domain: 공역 y
  • Image: 내부 계산
  • Range: 치역 y
• Linear Transformation 선형대수, 선형변환
  • input, output 벡터
  • 두 벡터를 계산한 결과를 변환한 것 == 두 벡터 변환한 결과를 계산한 것

선형변환 with Neural Networks

https://colah.github.io/posts/2014-03-NN-Manifolds-Topology/