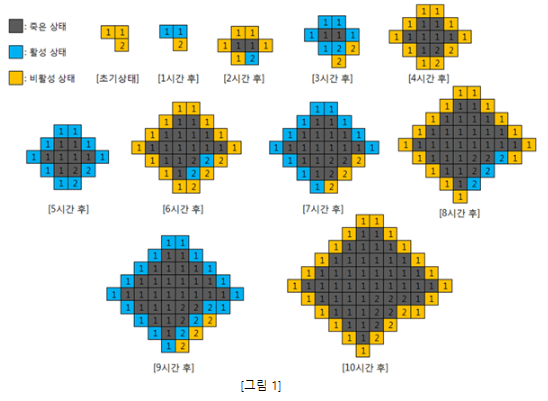
📌 문제
📌 문제 해석
해당 문제를 열어두고 같이 해석을 보는 것을 추천한다.
해당 문제는 모의 SW 역량테스트 문제로 아직까지 경험상 시간복잡도나 공간복잡도에 대한 최적화 문제보다는 구현에 가까운 문제들이 출제된다.
그래서 시간과 메모리에 대한 접근하기 전에 문제 주어진 조건을 파악하는 것을 우선시 했다.
1. 문제가 출력하기 원하는 것을 파악
해당 문제는 줄기세포 배양 시물레이션 프로그램을 만들고 싶어한다.
그리고 그 프로그램은 K시간을 주어졌을 때,
K 시간 후 "살아있는 줄기 세포" 의 총 갯수를 구하는 프로그램이다.
여기서 "살아있는 줄기 세포"는
비활성 상태인 줄기 세포와 활성 상태의 줄기 세포를 뜻한다.
2. 시물레이션 과정 파악
-
생명력 x
각 줄기세포는 생명력(x)를 가지고 있음
초기상태에서 줄기 세포들을 비활성 상태이다.만약 줄기세포가 x만큼의 생명력을 가지고 있다면 x시간 동안 비활성 상태였다가, x시간이 지나는 순간 활성 상태가 된다.
( x시간 비활성화 -> 활성화 )활성화 되고 나면 또 x시간 만큼 살아있다가
x시간이 지나면 세포는 죽게 된다.
( x시간 활성화 -> 죽음 )세포가 죽어도 소멸되는건 아니고, 죽은 상태로 셀을 차지하게 된다.
-
번식
활성화 된 줄기세포는 첫 1시간 동안 상하좌우 네방향으로 동시에 번식.번식된 줄기세포는 비활성 상태이다.
만약에 번식될 자리에 이미 다른 줄기세포가 존재하는 경우 번식하지 않는다.
하지만, 같은 시간에 두개 이상의 줄기세포가 동시에 번식하려는 경우에는
생명력 x 수치가 높은 줄기세포로 번식한다.
-
제약사항과 입력값을 확인
📖 제약사항
-
초기 상태에서 줄기 세포가 분포된 영역의 넓이는 세로 크기 N, 가로 크기 M이며 N, M은 각각 1 이상 50 이하의 정수
-
배양 시간은 K시간으로 주어지며 K는 1 이상 300 이하의 정수
-
배양 용기의 크기는 무한하다. 따라서 줄기 세포가 배양 용기 가장자리에 닿아서 번식할 수 없는 경우는 없다.
-
줄기 세포의 생명력 X는 1 이상 10 이하의 정수이다. (1≤X≤10)
✍ 입력
5 // TC 테스트 케이스 겟수 2 2 10 // 첫 번째 테스트 케이스: N=2, M=2, K=10 1 1 0 2 5 5 19 // 두 번째 테스트 케이스: N=5, M=5, K=19 3 2 0 3 0 0 3 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 2 -
- 과정을 파악한 것을 기반으로 설계
📌 설계
우선 필요한 데이터들이 많을 경우 class 화 하여 객체를 만들어 볼 것을 고민해본다.
특히 이렇게 구현이 복잡?하고 긴 문제들은 class 화 하여 들고 다니는 것이 정신건강에.. 좋은 것 같다..
그렇다면 해당 문제에서 필요한 class 는 줄기세포가 될 것이다.
이유는 문제를 보고 플랫하게 생각해보면, 결국 줄기세포가 들고 있어야 하는 정보가 많고, 해당 줄기세포에 따라서 계속 상태가 변하기 때문이다.
줄기세포 class 를 만든다면,
필요한 값은 줄기세포의 위치, 생명력x, 줄기세포의 상태(비활성화/ 활성화/죽음) 이다.
그리고 x 시간 동안 기다렸다가 활성화거나 죽기 때문에 int time 변수도 선언하여 상태를 변경해줄 수 있을 것이다!
더불어 제약사항을 보면, 배양 용기의 크기는 무한하다. 라는 문구가 있다.
나는 이 제약사항을 보고나서, 미리 배양 용기의 크기를 최대로 만들어두어야겠다고 생각했다.
공간적으로? 최악의 상황을 생각해보면,
x = 1일때, 아무래도 가장 많이 번식이 될 것이다.
그러면 x = 1일 때,
비활성화 -> 활성화 -> 죽음 단계에 이를 때를 보면,
비활성화 상태부터 죽을 때까지 2시간의 시간이 걸린다.
주어진 K 는 1 <= K <= 300 이기 때문에, 300이 최악의 경우라고 생각하면,
x = 1 이고 K가 300 일때, 4방으로 퍼진다고 생각하면,
300 / 2 만큼씩 사방으로 퍼지겠다!
그렇다면 결국 행은 N + K 이 될 것이고, 열은 M + K 이 될 것이다! 하지만 홀수일 경우를 생각해서 +1 씩 더 해준다.
행 = N + K + 1
열 = M + K + 1
그렇다면 매번 배열을 이렇게 넓게 설정해두면, 무한배양의 느낌을 가져갈 수 있다!
하지만 이렇게 될 경우 시간의 복잡도도 생각해봐야하는데,
N과 M이 제일 큰 경우는 50 이고, K는 300 이기 때문에
제일 최악의 경우 301 칸이 된다.
그렇게 크지 않기 때문에 사용 가능!!!
이렇게 기본 자료구조를 설정해 놓고나면, 이제 구현 방법을 생각해봐야 한다.
우리가 원하는건 결국
K시간을 주어졌을 때,
K 시간 후 "살아있는 줄기 세포" 의 총 갯수를 구하는 프로그램 이다.
그렇다고 하면,
큐를 사용하여, 모든 세포들을 담고,
큐에서 세포들을 꺼내면서, 상태를 확인 한후
비활성화 상태일 때, 상태일 때, 그리고 번식을 해야할 때 등 주어진 조건에 맞게 처리하고,
다시 큐에 넣어주면된다.
이때, 죽은 상태들은 다시 큐에 안넣어주면!!! 끝!!
하지면 여기서 어려운 부분은, 동시에 번식할 때
어떻게 생명력이 큰 애들만 넣어주지? 하는 점이다.
그래서 미리 전처리를 해준다! 미리 큐에 있는 애들을 돌면서, 미리 번식할 애들 중 큰 애를 미리 담아두는 것이다.
📌 코드
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.ArrayDeque;
import java.util.Queue;
import java.util.StringTokenizer;
import com.sun.jmx.remote.internal.ArrayQueue;
public class Solution {
static class Cell{
int r;
int c;
int x; // 생명력
int time;
int status; // 0. 비활성 / 1. 활성 / 2. 죽음
public Cell(int r, int c, int x) {
super();
this.r = r;
this.c = c;
this.x = x;
this.time = x;
}
void step() {
switch (status) {
case 0: // 비활성화 상태
if (--time == 0) // 생명력이 0이 되면? 활성화 상태로 바꿔주기
this.status = 1;
break;
case 1: // 활성화 상태
if (++time == x) // 생명력과 같아지면? 죽은 세포로 바꿔주기
this.status = 2;
break;
}
}
}
static BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
static StringTokenizer tokens;
static StringBuilder sb = new StringBuilder();
static int TC;
static int R,C,K;
static int[][] board;
static boolean[][] visited;
static int[] dr = {0,0,1,-1};
static int[] dc = {1,-1,0,0};
static Queue<Cell> q;
public static void main(String[] args) throws NumberFormatException, IOException {
TC = Integer.parseInt(br.readLine());
for(int t = 1; t <= TC; t++) {
tokens = new StringTokenizer(br.readLine());
R = Integer.parseInt(tokens.nextToken());
C = Integer.parseInt(tokens.nextToken());
K = Integer.parseInt(tokens.nextToken());
board = new int[R+K+1][C+K+1];
visited = new boolean[R+K+1][C+K+1];
q = new ArrayDeque();
// ---- 입력값 받을때, 큐에 넣어주고, visited 배열로 방문 표시도 해주기
for(int i = K/2+1 ; i < R+K/2+1; i++) {
tokens = new StringTokenizer(br.readLine());
for(int j = K/2+1; j < C+K/2+1; j++) {
int tmp = Integer.parseInt(tokens.nextToken());
if(tmp != 0) {
board[i][j] = tmp;
visited[i][j] = true;
q.offer(new Cell(i,j, tmp));
}
}
}
solve();
sb.append("#").append(t + " ").append(q.size()).append("\n");
}
System.out.println(sb);
}
private static void solve() {
while(K-- > 0) { // 주어진 K 시간 만큼 순회
// 이곳이 전처리 과정. 미리 생명력 수치가 높은 애들로 갱신
for(Cell test : q) { // 현재 큐의 모든 세포를 뽑아서 번식
if(test.status ==1) {
for (int d = 0; d < 4; d++) {
int nr = test.r + dr[d];
int nc = test.c + dc[d];
//방문 처리 => 이전 시간에 번식 된곳
if(visited[nr][nc])
continue;
//배양 용기의 세포 생명력만 갱신 : 수치가 가장 높은 값으로
if(board[nr][nc]<test.x)
board[nr][nc] = test.x;
}
}
}
int size = q.size();
for(int s = 0; s < size; s++) {
Cell current = q.poll();
if(current.status == 1) {
// 활성화 상태면 사방 번식
for(int i = 0; i < 4; i++) {
int rx = current.r + dr[i];
int ry = current.c + dc[i];
if(visited[rx][ry]) continue;
// 큐에 넣을때, 미리 갱신해둔 생명력으로 넣어주기.
q.offer(new Cell(rx,ry, board[rx][ry]));
visited[rx][ry] = true;
}
}
//status 처리 함수 호출
current.step();
// 죽었으면 continue
if(current.status == 2) {
continue;
}
// 비활성화거나 활성화니까 다시 큐에 넣어주기!
q.offer(current);
}
}
}
}
📌 메모리 / 시간
49,100 kb
228 ms
