주어진 nxn 크기의 흑백 이미지에서 검은 점을 포함하지 않는 가장 큰 빈 정사각형을 구하는 문제이다.
재귀적 서술
m x m 크기의 픽셀로 이루어진 정사각형 S가 비어있다면 다음이 성립
- S의 가장 우측 하단의 픽셀이 비어있다.
- 좌측상단, 좌측하단, 우측상단의 크기 (m-1)x(m-1) 정사각형이 비어있다.

동적계획법
- LES(x,y): (x,y)를 우측하단 꼭지점으로 하는 최대 정사각형의 크기
다음이 성립
- 픽셀 (x,y)가 비어있지 않다면 LES(x,y) = 0
- 첫번째 행 또는 열의 픽셀 (x,y)가 비어있다면 LES(x,y) = 1
- 나머지 픽셀 (x,y)가 비어있다면
LES(x,y) = min(LES(x-1,y-1), LES(x,y-1), LES(x-1, y)) +1
void LES(int n)
{
for(int x=1; x<n; x++)
{
for(int y=1; y<n; y++)
{
if((x,y) is not empty) // 비어있지 않다면
LES[x,y] = 0;
else if(x=1 or y=1) // 첫 번째 행 또는 열이 비어있다면
LES[x,y] = 1;
else // 그 외 픽셀 (x,y)가 비어있다면
LES[x,y] = min(LES[x-1,y-1], LES[x,y-1], LES[x-1,y]) + 1;
}
}
}다음과 같은 정사각형이 있다. 검정색 칸은 비어있지 않은 칸이다.
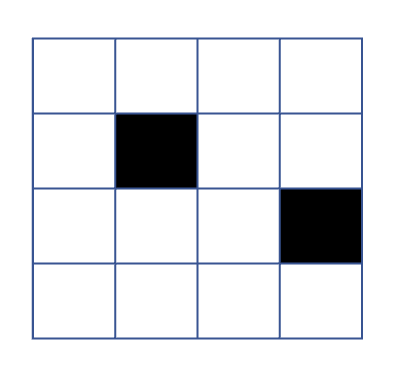
먼저 비어있는 첫번째 행과 열을 모두 1로 채웠고, 비어있지 않은 칸을 0으로 채웠다.
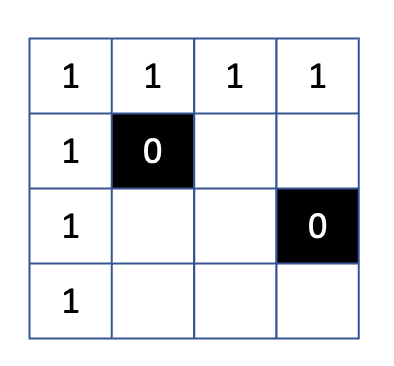
그리고 나머지 비어있는 칸에 대해
대각선(x-1, y-1), 왼쪽(x-1, y), 위쪽(x, y-1) 중 가장 작은 값에다가 1을 더한 값을 채워주었다.
편집거리를 구할 때와 같은 방식이었다.
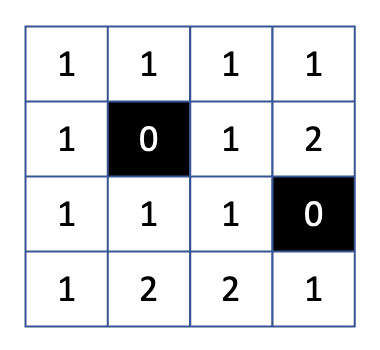
2가 있는 칸을 보면, 해당 칸을 우측하단 꼭지점으로 하는 2x2 크기의 공백인 정사각형이 존재함을 확인할 수 있다.
대각선, 왼쪽, 위쪽의 값들은 이미 자신까지의 최대공백 정사각형의 크기를 가지고 있기 때문에,
또 다른 빈 칸의 값을 채울 때 해당 값들 중 가장 작은 값에 +1 해주면 되었다.
만약 DP의 점화식이 없었다면,, 어떻게 풀어야할지 감도 안온다.
한 칸씩 더 늘려보았다.
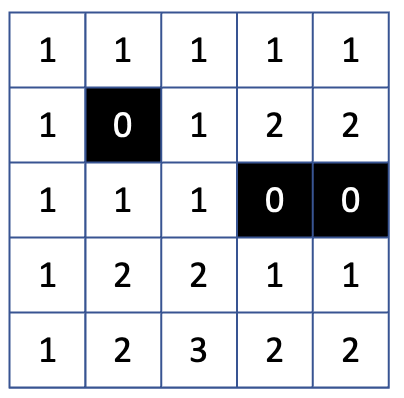
첫번째 행과 첫번째 열에 1을 채우는 이유는
'내 옆이나 위에 더 이상 칸 없어서 나 한 칸이 최대야~'라고 말해주는 것 같고,
비어있지 않은 칸에 0을 채우는 이유는
주변 칸에다가 '나 때문에 최대 공백이 이어질 수 없고 다시 시작해야 해~'하고 말해주는 것 같고,
나머지 칸이 비어있을 경우에는
'왼쪽, 대각선, 오른쪽 애들 중에서 내가 이어 만들 수 있는 공백 정사각형을 찾아야지~' 하는 것 같다.
이 때 혼자 생각하면 어려웠을 것 같은 부분이 최소값을 가져오는 것이라서 이유를 생각해보았다.
이들 중 최소값을 가져와야하는 이유는 세 개의 숫자가 모두 같은 경우가 아니라면
어느 한 쪽 방향에서 막힌 칸이 있다는 의미이기 때문이다.
