Select Working Days
- 입력 배열 D는 N Days에 대하여 해당 날에 일했을 때 벌 수 있는 돈이 적혀있다.
- One Rule: 연속으로 일할 수 없다.
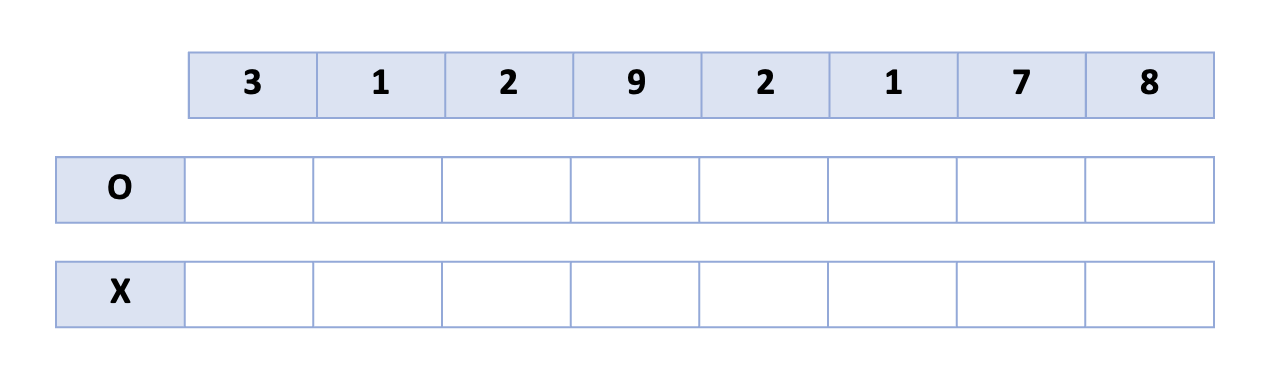
위와 같은 표를 채워나가면서 문제를 풀 것이다.
O 배열에는 오늘(i) 일했을 때 오늘까지 벌 수 있는 가장 많은 돈을 적고,
X 배열에는 오늘(i) 일하지 않았을 때 오늘까지 벌 수 있는 가장 많은 돈을 적을 것이다.
포인트는
O 배열에는 연속으로 일할 수 없기 때문에 i-1 Day에서 반드시 X배열의 값을 가져와서 i의 값을 더해주어야 할 것이다.
X 배열에는 i-1 Day에 일을 해도 되고, 안해도 되기 때문에 i-1의 O배열의 값과 X배열의 값 중 더 큰 값을 가져오면 된다.
점화식으로 나타내면 다음과 같다.
O[i] = X[i-1] + D[i]
X[i] = max(O[i-1], X[i-1])
위 점화식에 따라 배열을 채우면 다음과 같다.
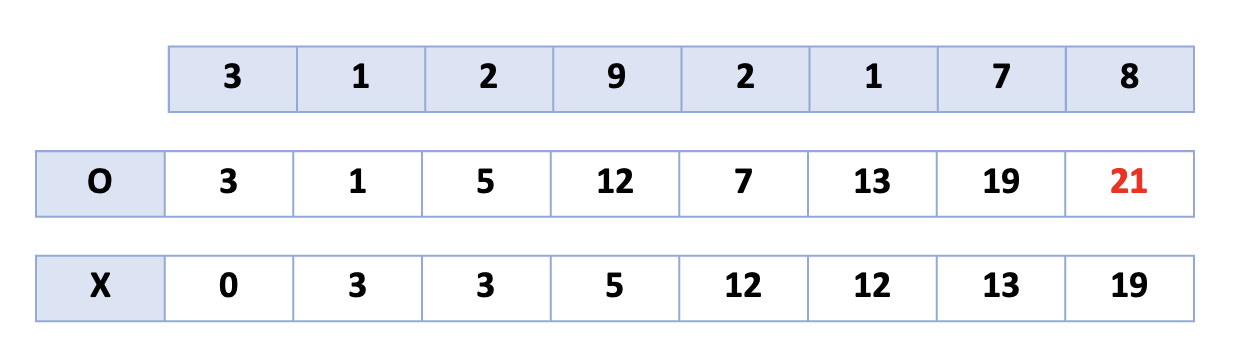
일할 날을 잘 골랐을 때 벌 수 있는 가장 많은 돈은
마지막날의 O와 X중 더 큰 값일 것이고 위 예시에서는 21이 된다.
코드
int W(int a[], int n)
{
int D[n+1][2];
D[1][0] = 0; // X
D[1][1] = a[1]; // O
for(int i=1; i<=n; i++)
{
D[i][0] = max(D[i-1][0], D[i-1][1]);
D[i][1] = D[i-1][0] + a[i];
}
return max(D[n][0], D[n][1]);
}해당 문제에서 DP를 쓸 수 있는 이유는 무엇일까?
만약 n에 대해 일을 하고 안하는 경우의 수를 다 따져서 했다면 시간이 2^n 정도 되었을 것이다.
그런데 O, X 배열을 만들어서 앞 쪽부터 값을 채웠을 때
이후의 값들은 점화식을 따라 앞의 값을 가져와서 채워줄 수 있어서 시간을 단축할 수 있었다.
정리하자면 점화식을 통해
배열을 채우는 순서를 정하고, 이후 채워진 배열의 값을 가져다 쓸 수 있었기 때문에 DP로 풀 수 있었다고 생각된다.
여기까지 쓰고 백준에서 DP 문제 중 '퇴사'를 풀다가 2시간을 날렸다,,
근데 아직 이해 못했는데 배열을 뒤에서부터 채울 수도 있는 케이스를 봤다.
https://www.acmicpc.net/problem/14501
점화식을 세우면서 dp 배열에 무슨 값을 적을 것인지, 어떤 순서로 적을 것인지 중요하다는 것도 배웠다.
