신경망의 깊이가 깊어질수록 학습이 어렵다는 문제를 해결해주는 highway network를 소개하는 논문입니다. highway network는 ELMo 논문에서 활용된다고 언급되어 있습니다.
[Abstract]
다양한 이론과 실증적 연구를 통해 신경망의 깊이가 중요한 성공의 요인이란 것이 알려졌습니다. 하지만 신경망 학습은 신경망의 깊이가 깊어질수록 어려워지고 매우 깊은 신경망을 잘 학습하는 것은 여전히 많은 관심을 받는 분야입니다. 해당 논문에서는 매우 깊은 신경망에서 gradient-based 학습을 쉽게 해주는 구조를 소개합니다. 해당 논문에서 소개하는 구조는 몇몇 layer에서 information이 따로 간섭을 받지 않은 채 전달되기 때문에 highway network라고 합니다. Highway network는 network를 통해 information의 흐름을 regulate하는 것을 학습하는 gating unit을 사용하는 특징을 지니고 있습니다. 수백 개의 layer를 지닌 highway network는 stochastic gradient descent와 다양한 activation function을 사용하여 학습될 수 있습니다.
1. Introduction
Supervised machine learning에서 최근 실증적인 발전이 깊은 신경망을 통해 이루어졌습니다. 이러한 성공에 있어 network의 깊이(computation layer들의 연속)가 주요한 역할을 하였습니다.
이론 측면에서, 깊은 신경망이 얕은 신경망보다 특정 함수들의 종류들을 더 효율적으로 표현할 수 있다는 것이 알려졌습니다. 깊은 신경망을 활용하여 복잡한 task에서 computational, statistical 효율성을 얻을 수 있었습니다.
하지만 깊은 신경망을 학습하는 것은 단순히 layer를 추가하는 것과 같이 단순하지 않습니다. 깊은 신경망을 최적화하는 것은 여전히 매우 어려운 문제라고 알려져있습니다.
해당 논문에서는 어떠한 깊이의 신경망이더라도 최적화활 수 있는 구조를 소개합니다. 이는 LSTM에서 영감을 받은 information flow를 regulating할 수 있는 학습된 gating mechanism을 활용하여 달성할 수 있었습니다. Gating mechanism 덕분에 신경망은 information이 몇몇 layer에서는 정보의 손실없이 그대로 흐를 수 있는 path를 가질 수 있게 되었습니다. 해당 논문에서는 이러한 path를 information highway라 이름 붙이고 이 path를 갖는 network를 highway network라고 부릅니다.
실험을 통해 해당 논문에서는 highway network는 SGD(Stochastic Gradient Descent) with momentum을 통해 900개의 layer를 지닌 매우 깊은 신경망까지 최적화될 수 있다는 것을 보였습니다. 해당 논문에서는 highway network의 최적화는 깊이와 관련이 없다는 것을 보였습니다. 기존의 network에서는 layer의 수가 증가할 수록 문제가 있었습니다.
1.1 Notation

2. Highway Networks
plain feedforward neural network는 일반적으로 L개의 layer로 이루어져 있으며 각 layer들은 W_H,l 을 parameter로 사용하는 nonlinear transform H에 input x_l를 받아 output y_l를 만듭니다. 즉, 신경망 전체로 보았을 때, x_1은 신경망의 input이 되고 y_L은 신경망의 output이 됩니다.

H는 일반적으로 affine transform이고 그 후 non-linear activation function이 적용됩니다.
Highway network에서는 2개의 nonlinear transform T(x, W_T)와 C(x, W_C)를 추가로 정의합니다.

T는 transform gate, C는 carry gate라고 부릅니다. 왜냐하면 ouput을 만들 때 T는 얼만큼 input을 변화시킬 것인가, C는 얼만큼 input을 그대로 전달할 것인가를 결정하기 때문입니다. 해당 논문에서는 단순화를 위해 C = 1-T로 두어 설명을 진행합니다.
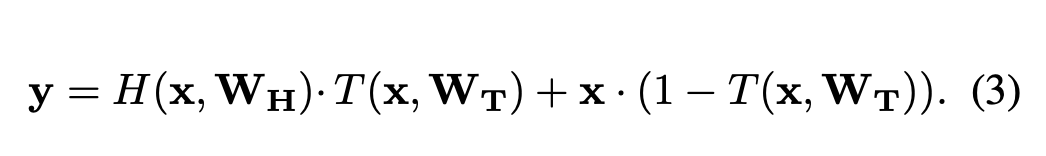
식(3)을 만족시키기 위해 x, y, H(x, W_H), T(x, W_T)의 차원은 모두 동일해야합니다. 이러한 layer transformation의 re-parameterization은 식(1)과 비교하였을 때 더욱 유연합니다.
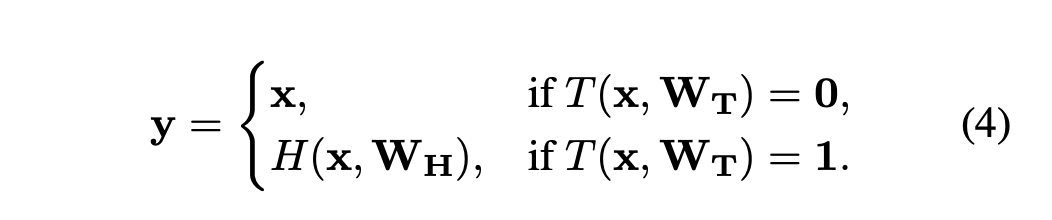
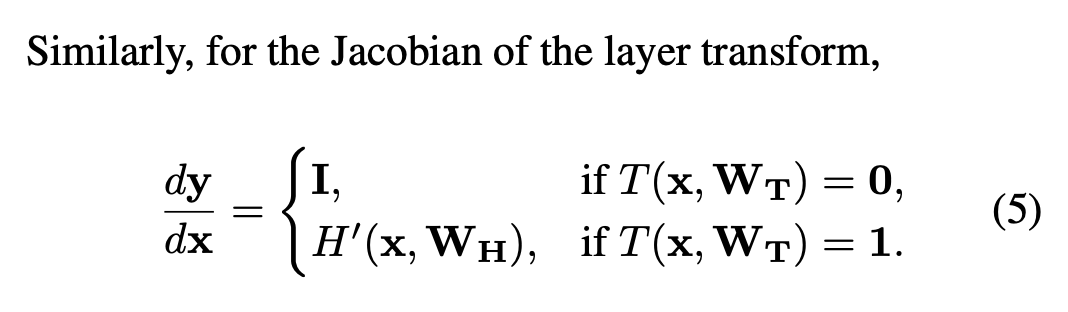
위 2개의 식을 보면 transform gate의 결과에 의하여 highway layer는 plain layer와 input을 단순히 그대로 흘리는 2가지 역할 사이를 자연스럽게 선택하여 사용할 수 있습니다. Highway network는 i번째 block이 block state H_i(x)와 transform gate output T_i(x)를 계산하는 multiple block으로 이루어져 있습니다. 결과적으로 highway network는 block output y_i를 얻어 다음 layer로 보냅니다.

2.1 Constructing Highway Networks
식(3)은 x, y, H(x, W_H), T(x, W_T)의 차원이 모두 동일해야만 합니다. Representation의 size를 바꿔야될 필요성이 있을 때, x에 sub-sampling이나 padding을 활용하여 x'을 만들 수 있습니다. 또 다른 대안으로는 highway가 없는 plain layer를 활용하여 차원을 바궈준 후 highway layer를 다시 쌓아줍니다.
2.2 Training Deep Highway Networks
plain deep network에서 SGD를 활용한 학습은 forward, backward propagation의 분산이 일정하게 유지하는 등의 적절한 가중치 초기화 전략을 사용하지 않는다면 제대로 수행되지 않게됩니다. 이러한 초기화는 H의 정확한 형태에 영향을 받습니다.
Highway layer에서는 T(x) = sigma((W_T)^T * x + b_T)로 정의된 transform gate를 사용합니다. 이 때 W_T는 weight matrix이고, b_T는 bias vector입니다. 이는 초기화전략이 H의 특성과 관련이 없다는 것을 제안합니다. b_T는 negative value로 초기화될 수 있습니다.
해당 논문 실험에서 negative bias 초기화는 평균이 0인 초기 분포를 따르는 W_H와 다양한 activation function을 활용하는 H를 사용하는 매우 깊은 network 학습에서 충분히 활용될 수 있다는 것을 보였습니다.
3. Experiments
3.1 Optimization
매우 깊은 신경망은 variance-preserving 초기화 전략을 사용하더라도 최적화가 쉽지 않습니다.
해당 논문에서는 plain network와 highway network를 다양한 깊이에서 학습을 시켰습니다.
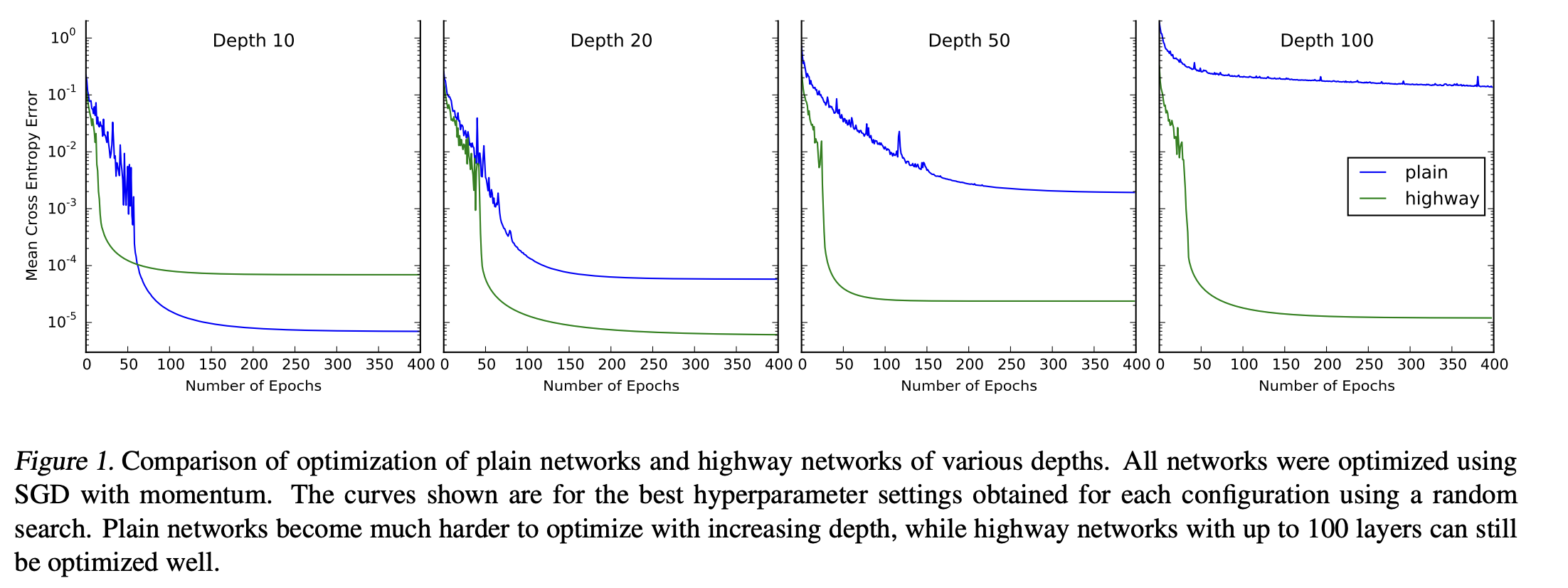
10개의 layer의 plain network는 좋은 성능을 보였지만 깊이가 깊어질수록 성능이 눈에띄게 감소하였습니다. Highway network는 하지만 깊이가 깊어져도 큰 영향을 받지 않았습니다.
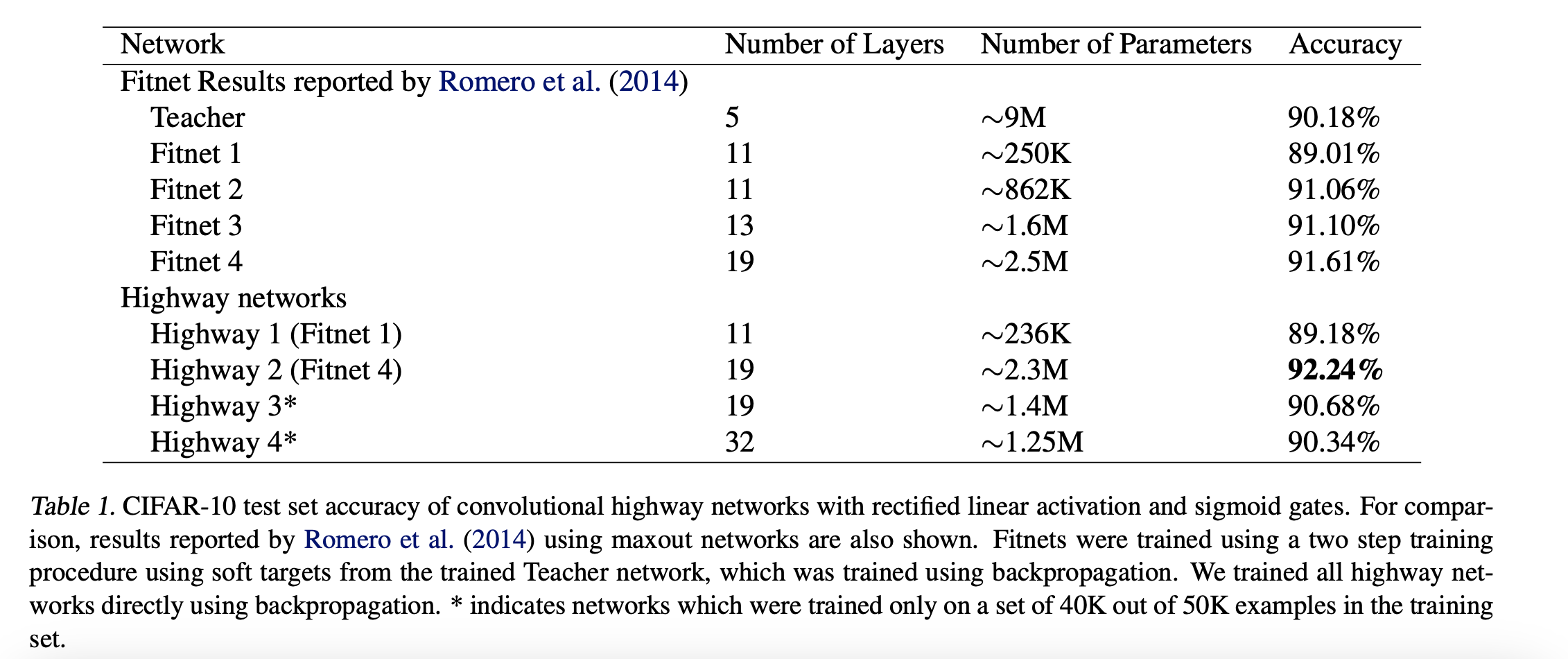
3.2 Comparison to Fitnets
Deep highway network는 쉽게 최적화되지만 test set에서도 좋은 성능을 유지한 채로 쉽게 최적화가 될 수 있을까?
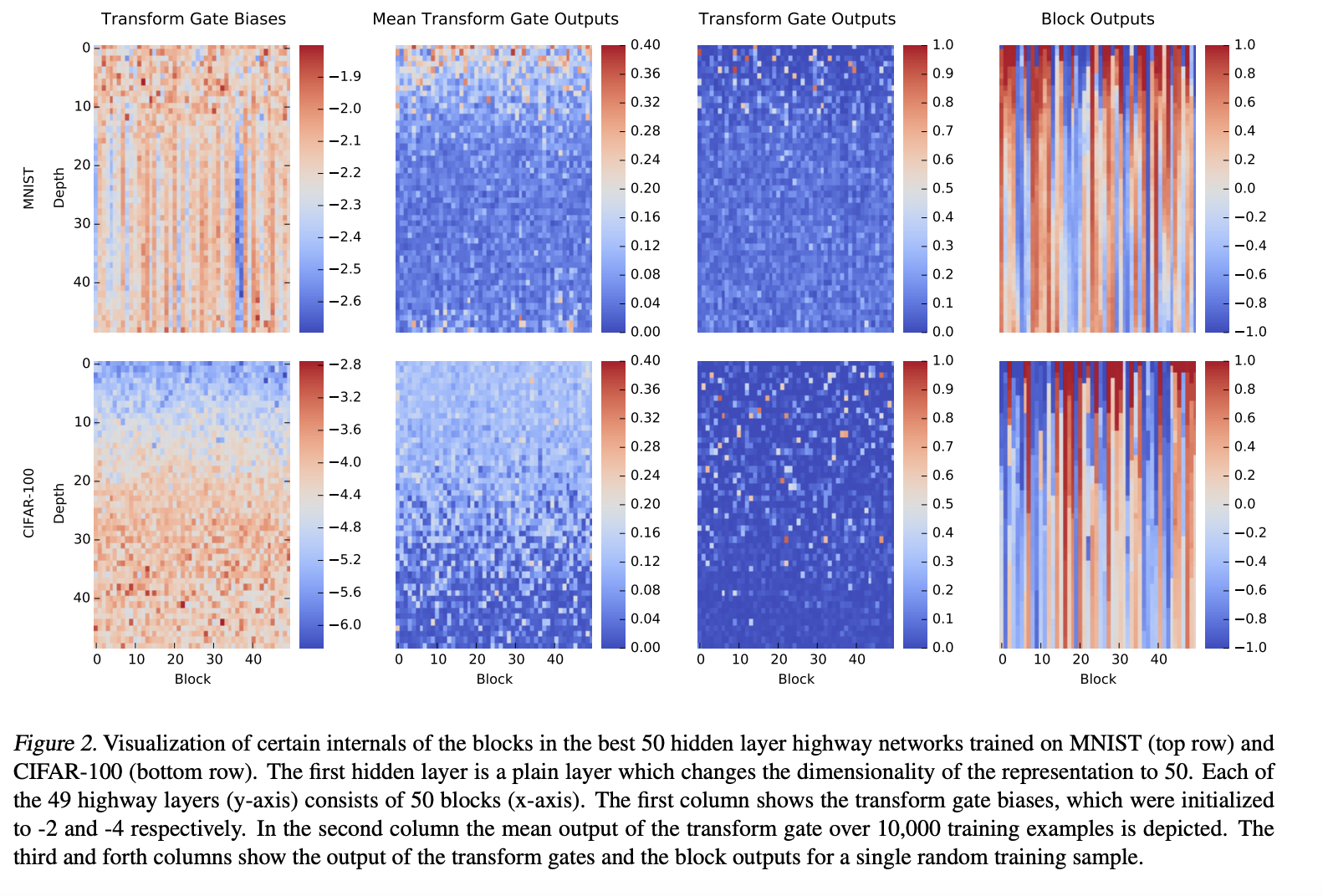
4. Analysis
5. Conclusion
신경망을 통해 information의 route를 학습하는 것은 학습을 손쉽게 하여 신경망이 가질 수 있는 문제에 도전하여 신경망이 적용될 수 있는 분야의 scale up에 도움을 줍니다. 매우 깊은 신경망을 학습하는 것은 여전히 어렵습니다.
Highway network는 매우 깊은 신경망을 simple SGD를 통해서도 학습할 수 있도록 해주는 새로운 구조입니다. 기존의 plain neural 구조가 신경망의 깊이가 깊어질수록 학습에 어려움을 겪지만 해당 논문의 실험에서는 highway network는 network의 layer가 수백개가 되더라도 어떠한 영향도 받지 않는 다는 것을 보였습니다.