문제
N×N개의 수가 N×N 크기의 표에 채워져 있다. (x1, y1)부터 (x2, y2)까지 합을 구하는 프로그램을 작성하시오. (x, y)는 x행 y열을 의미한다.
예를 들어, N = 4이고, 표가 아래와 같이 채워져 있는 경우를 살펴보자.
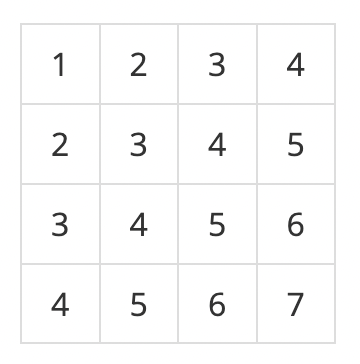
여기서 (2, 2)부터 (3, 4)까지 합을 구하면 3+4+5+4+5+6 = 27이고, (4, 4)부터 (4, 4)까지 합을 구하면 7이다.
표에 채워져 있는 수와 합을 구하는 연산이 주어졌을 때, 이를 처리하는 프로그램을 작성하시오.
입력
첫째 줄에 표의 크기 N과 합을 구해야 하는 횟수 M이 주어진다. (1 ≤ N ≤ 1024, 1 ≤ M ≤ 100,000) 둘째 줄부터 N개의 줄에는 표에 채워져 있는 수가 1행부터 차례대로 주어진다. 다음 M개의 줄에는 네 개의 정수 x1, y1, x2, y2 가 주어지며, (x1, y1)부터 (x2, y2)의 합을 구해 출력해야 한다. 표에 채워져 있는 수는 1,000보다 작거나 같은 자연수이다. (x1 ≤ x2, y1 ≤ y2)
출력
총 M줄에 걸쳐 (x1, y1)부터 (x2, y2)까지 합을 구해 출력한다.
예제 입/출력
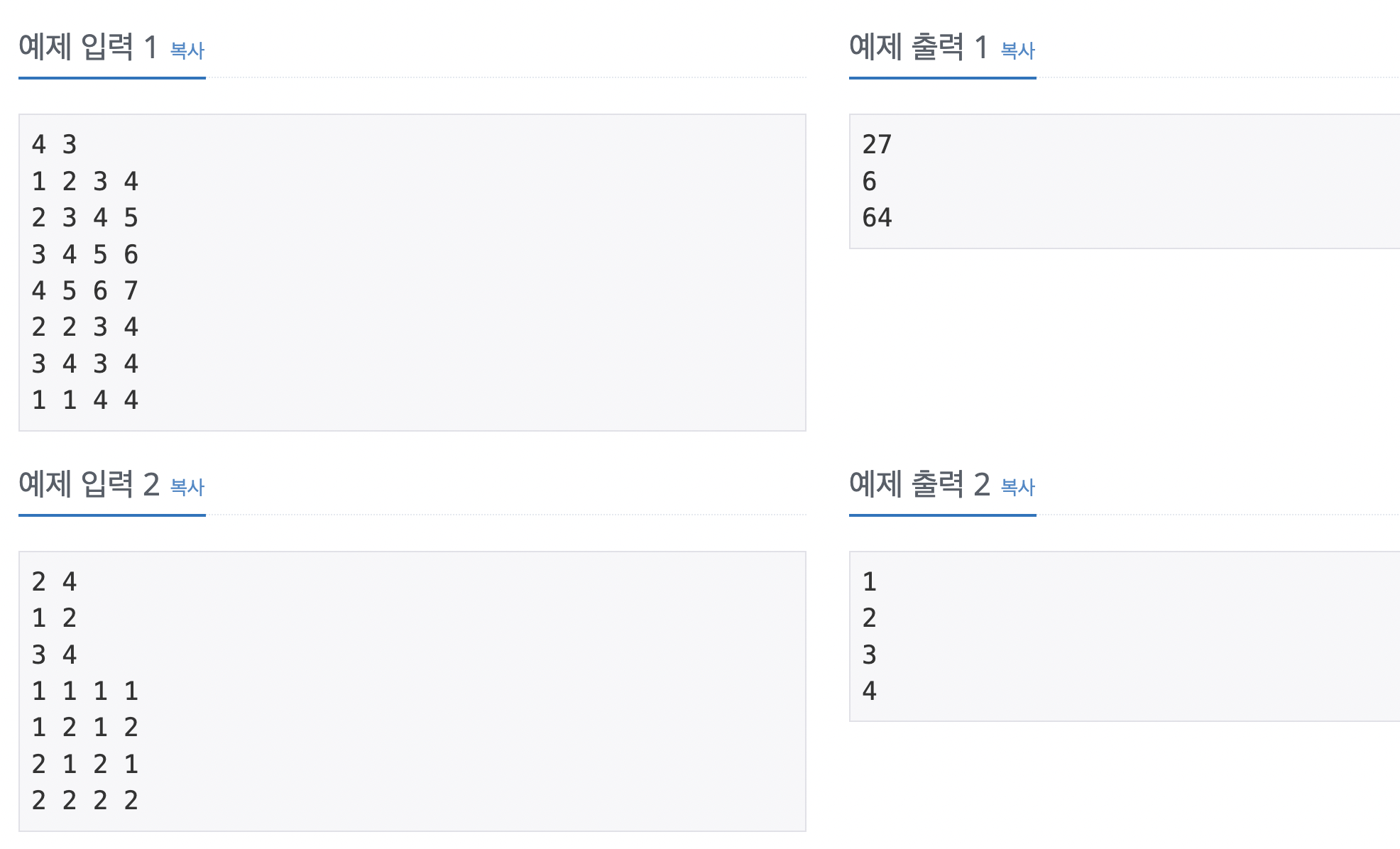
나의 풀이
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.StringTokenizer;
import java.io.IOException;
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader bufferedReader = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer stringTokenizer = new StringTokenizer(bufferedReader.readLine());
int arrSize = Integer.parseInt(stringTokenizer.nextToken()) + 1;
int queryNum = Integer.parseInt(stringTokenizer.nextToken());
long[][] S = new long[arrSize][arrSize];
for (int i = 1; i < arrSize; i++) {
stringTokenizer = new StringTokenizer(bufferedReader.readLine());
for (int j = 1; j < arrSize; j++) {
if (i == 1 && j == 1) {
S[i][j] = Integer.parseInt(stringTokenizer.nextToken());
} else if (i == 1) {
S[i][j] = S[i][j - 1] + Integer.parseInt(stringTokenizer.nextToken());
} else if (j == 1) {
S[i][j] = S[i - 1][j] + Integer.parseInt(stringTokenizer.nextToken());
} else {
S[i][j] = S[i - 1][j] + S[i][j - 1] - S[i - 1][j - 1] + Integer.parseInt(stringTokenizer.nextToken());
}
}
}
for (int q = 0; q < queryNum; q++) {
stringTokenizer = new StringTokenizer(bufferedReader.readLine());
int x1 = Integer.parseInt(stringTokenizer.nextToken());
int y1 = Integer.parseInt(stringTokenizer.nextToken());
int x2 = Integer.parseInt(stringTokenizer.nextToken());
int y2 = Integer.parseInt(stringTokenizer.nextToken());
long result = S[x2][y2] - S[x2][y1 - 1] - S[x1 - 1][y2] + S[x1 - 1][y1 - 1];
System.out.println(result);
}
}
}예시 풀이
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.StringTokenizer;
public class P11660_구간합구하기2 {
public static void main(String[] args) throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
int N = Integer.parseInt(st.nextToken());
int M = Integer.parseInt(st.nextToken());
int A[][] = new int[N + 1][N + 1];
for (int i = 1; i <= N; i++) {
st = new StringTokenizer(br.readLine());
for (int j = 1; j <= N; j++) {
A[i][j] = Integer.parseInt(st.nextToken());
}
}
int D[][] = new int[N + 1][N + 1];
for (int i = 1; i <= N; i++) {
for (int j = 1; j <= N; j++) {
//부분 합 구하기
D[i][j] = D[i][j - 1] + D[i - 1][j] - D[i - 1][j - 1] + A[i][j];
}
}
for (int i = 0; i < M; i++) {
st = new StringTokenizer(br.readLine());
int x1 = Integer.parseInt(st.nextToken());
int y1 = Integer.parseInt(st.nextToken());
int x2 = Integer.parseInt(st.nextToken());
int y2 = Integer.parseInt(st.nextToken());
// 부분 합 배열을 이용한 질의 답변하기
int result = D[x2][y2] - D[x1 - 1][y2] - D[x2][y1 - 1] + D[x1 - 1][y1 - 1];
System.out.println(result);
}
}
}리뷰
꽤나 헤맨 문제였다.
처음에는 1차원 배열 S를 선언하여 S[x * arrSize + y]를 서로 빼서 구하는 방식으로 코드를 짰는데, 일단 그렇게 구현하면 기본적으로 Query의 최대 갯수 100000과 arrSize의 최대 갯수 1024를 구하면 1억이 넘으므로 시간 제한 1초보다 오래 걸리게 된다.
결국 혼자서 많이 헤매다가 힌트를 보게 되었는데, 내가 생각하지 못하는 방식으로 구간 합 2차원 배열을 구현하여, 전체 사각형에서 특정 부분을 빼서 정답인 사각형을 구하는 방식이었다.
지금 보니 굳이 if/else if 문으로 나눌 필요 없이 간단하게 정리할 수 있던 부분을 발견했다. 아쉬움이 많이 남는 문제이다. 적어도 해당 알고리즘이라도 완벽하게 이해하여 나중에 비슷한 문제가 나오면 바로 적용해보도록 하자.
또 하나 생각해 둘 것. 문제에 나오는 변수 이름을 그대로 쓰도록 노력해보자.
