BaekJoon - 11660

​
11660번: 구간 합 구하기 5
​

구간 합 구하기 5

​
N x N 배열의 (x1, y1)에서 (x2, y2)까지 합을 구하는 프로그램을 만들기
​
예) N=4 표처럼 아래가 채워져 있다.
​

​
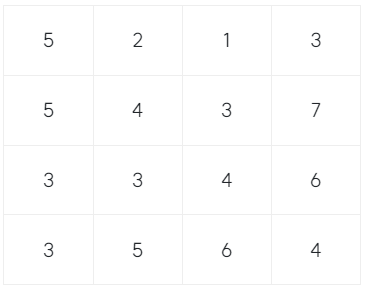
여기서 (2,2)부터 (4,3)까지 합을 구하면 (4 + 3 + 7) + (3 + 4 + 6)하면 27이다.
​

나의 방식

​

접근 방식

​
바로 전의 문제에서 합의 배열을 구현하는 방식으로 문제를 풀었기에 합의 배열을 이용하는 방식을 사용하기로 함
​
1차원 합의 배열을 이어 만든 2차원 합의 배열을 하나의 축을 중심으로 만들고자 함
​

​
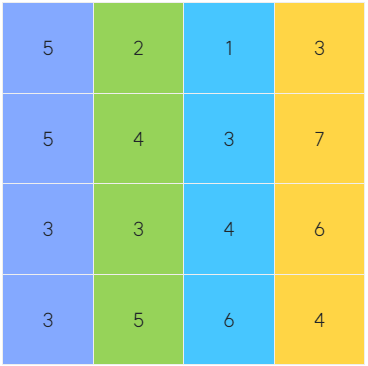
int [][]의 2차원 배열을 x축을 기준으로 2차원 합의 배열의 형태로 만들기로 함
​

​
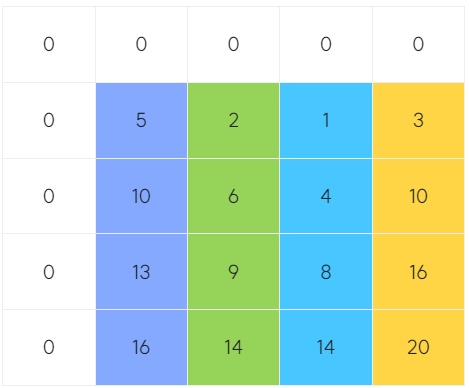
여기서 0을 채움 원래 N x N 이 아닌 (N + 1) x (N + 1)의 형태인데 1~1번째 즉 (x1, y1) ~ (x1, y1)의 구간인 (x1, y1)와 같은 값을 구하기에 필요하기 때문이다.
​
이후 입력받은 구간 x1 ~ x2까지 for문으로 받고 y2 - (y1 - 1)으로 해결하면 된다고 생각함
​

구현

​

슈도 코드

​
책을 통해 본 방식에서 나름의 한글로 적은 코드(슈도 코드)를 만들어 보는 방식을 했고 나도 따라 하면서 조금 배우는 것이 있었기에 그대로 적어보려고 한다.
​

숫자 2개 N, M 입력 받기
N * N 배열 생성 (int형)
입력 받아 배열에 넣기 (2중 for문) [][] <- [x][y]라고 생각하기
​
[x]축을 기준으로 합배열[][] S문 만들기 (long형)
 - 배열 크기 N + 1 해주기 
 - 인덱스 0인 곳 비워두고 1인 곳 부터 넣기
 - for문 (i = 1, i < N + 1, i++)
 - S[i][j] = sum[i][j - 1] + array[i - 1][j - 1];
​
​
(X1, Y1) (X2, Y2) 입력받는 for문 작성 (i < M) {
    퀴즈 입력 받기
    for 문 (i = X1, i <= X2, i++) {
        sum += S[Y2] - S[Y1 - 1];
    }
    빌더.append(sum)
}
출력

​

코딩

​

import java.io.*;
import java.util.StringTokenizer;
​
public class Main {
    public static void main(String[] args) throws IOException {
​
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
        StringBuilder sb = new StringBuilder();
​
        StringTokenizer stringTokenizer = new StringTokenizer(br.readLine(), " ");
        int sizeNum = Integer.parseInt(stringTokenizer.nextToken());
        int quizNum = Integer.parseInt(stringTokenizer.nextToken());
​
        int[][] array = new int[sizeNum][sizeNum];
​
        for (int i = 0; i < sizeNum; i++) { // 배열 값 입력
            stringTokenizer = new StringTokenizer(br.readLine(), " ");
            for (int j = 0; j < sizeNum; j++) {
                array[i][j] = Integer.parseInt(stringTokenizer.nextToken());
            }
        }
​
        long[][] sumArray = new long[sizeNum + 1][sizeNum + 1];
​
        for (int i = 1; i < sizeNum + 1; i++) {
            for (int j = 1; j < sizeNum + 1; j++) {
                sumArray[i][j]  = sumArray[i][j - 1] + array[i - 1][j - 1];
            }
        }
​
        for (int q = 0; q < quizNum; q++) {
            stringTokenizer = new StringTokenizer(br.readLine(), " ");
            int X1 = Integer.parseInt(stringTokenizer.nextToken());
            int Y1 = Integer.parseInt(stringTokenizer.nextToken());
            int X2= Integer.parseInt(stringTokenizer.nextToken());
            int Y2 = Integer.parseInt(stringTokenizer.nextToken());
​
            long sum = 0;
            for (int i = X1; i <= X2; i++) {
                sum += sumArray[i][Y2] - sumArray[i][Y1 - 1];
​
            }
            sb.append(sum).append("\n");
        }
​
        bw.write(sb.toString());
        bw.flush();
        br.close();
​
    }
}

​
답을 구하는 데는 성공했지만 방법이 잘못된 방식이다. 다른 정답들에 비해 속도가 너무 느리다.
​

책의 방식

​

두 축을 모두 고려한 합배열 만들기

​
책의 방식을 읽고 나서야 배열의 사용 이유가 떠올랐다. for문이나 이런 과정 없이 배열은 빠르게 값을 받아와서 연산하는 데 있다는 것을 까먹었었다. 단순히 문제만 풀려고 생각했기에 가장 중요한 것을 놓친 것 같다.
​
배열의 빠른 검색을 생각하면 (x1, y1)과 (x2, y2)를 입력받아서 (x2, y2) - (x1, y1)의 값을 계산하는 것으로 바로 답을 받아야만 했다. 즉 x축 y축 모든 것을 합한 2차원 합배열을 만들어야 했다.
​
합집합 S[x][y]의 값은 (1, 1)에서 (x, y)의 모든 값들을 합한 값이어야 한다. 이는 S[x-1][y]와 S[x][y -1]그리고 (x, y)의 값으로 구할 수 있다. 나는 예시와 그림으로 쉽게 이해할 수 있었다.
​
S[x][y] = S [3][3]이라면 S[2][3]의 값과 S[3][2]의 값을 더해서 만든다고 생각하면 될 것이다.
​

​
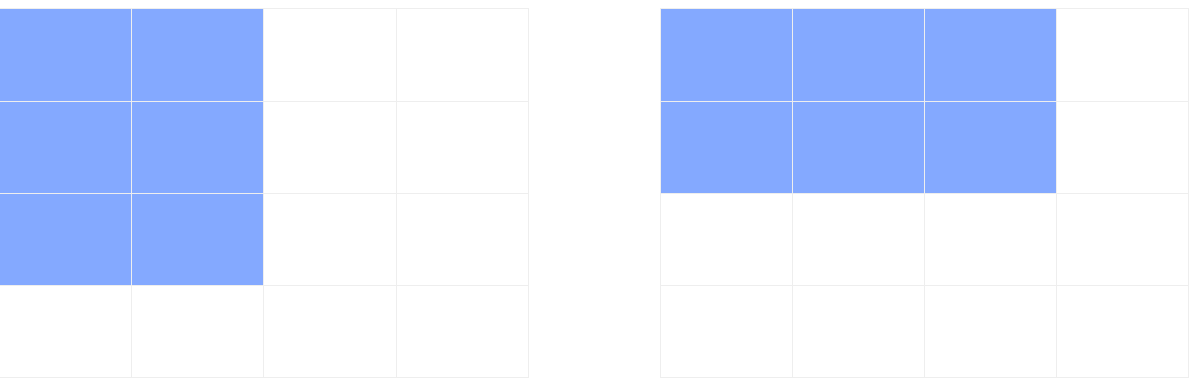
겹치는 부분을 빼주고 더하지 않은 부분을 더하면 된다.
​

​
이를 식으로 만들어 본다면 ( (x, y)는 array의 A[x][y]로 표시한다 )
​
S[x][y] = S[x-1][y] + S[x][y-1] - S[x-1][y-1] + A[x][y]
​

코딩

​

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;
​
public class Book_11660 {
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer stringTokenizer = new StringTokenizer(br.readLine(), " ");
        int N = Integer.parseInt(stringTokenizer.nextToken());
        int M = Integer.parseInt(stringTokenizer.nextToken());
​
        int[][] A = new int[N + 1][N + 1];
        for (int i = 1; i <= N; i++) {
            stringTokenizer = new StringTokenizer(br.readLine(), " ");
            for (int j = 1; j <=N ; j++) {
                A[i][j] = Integer.parseInt(stringTokenizer.nextToken());
            }
        }
        int[][] D = new int[N + 1][N + 1];
        for (int i = 1; i <= N; i++) {
            for (int j = 1; j <= N; j++) {
                // 구간 합 구하기
                D[i][j] = D[i][j - 1] + D[i - 1][j] - D[i - 1][j - 1] + A[i][j];
            }
        }
​
        for (int i = 0; i < M; i++) {
            stringTokenizer = new StringTokenizer(br.readLine(), " ");
            int x1 = Integer.parseInt(stringTokenizer.nextToken());
            int y1 = Integer.parseInt(stringTokenizer.nextToken());
            int x2= Integer.parseInt(stringTokenizer.nextToken());
            int y2 = Integer.parseInt(stringTokenizer.nextToken());
​
            int result = D[x2][y2] - D[x1 - 1][y2] - D[x2][y1 - 1] + D[x1 - 1][y1 - 1];
            System.out.println(result);
        }
    }
}

​

생각

​
합배열을 여러번 만들어 봤는데 합배열의 크기를 정하는 것도 중요하다. (1, 1) ~ (1, 1)을 범위를 구하는 상황에서 만약에 배열의 크기를 N x N과 같이 똑같이 만든다면 S[x - 1][y]와 같은 부분에서 index의 값이 -1이 들어가는 상황이 자주 발생하게 된다. 이를 예외적으로 밖으로 빼줘서 if로 처리해도 되지만 if는 최대한 지양하는게 가장 좋기에 이런 부분을 신경써주는 것이 좋다.
​
2차원 배열을 만들면서 드는 생각이 나는 굉장히 단순하다는 것이다. 그냥 배운 것을 연속으로 붙여서 이 문제를 해결했다는 것만 봐도 내 생각이 짧은 것이 잘 보인다. 문제를 해결하는 것만 중요한 것이 아닌 배열을 왜 사용하는지 조금만 고민해봤어도 알 수있는 문제였기에 더욱 바보같이 느껴진다.
​
배열은 검색이 빠르다 즉 빠르게 검색해서 빠르게 연산하는 것이 목표인데 내 방식은 원하는 범위를 받을 때마다 계속해서 for문을 통해서 연산해줘야한다. 그에반해 정답은 한번의 합배열을 만드는 for문 이후에는 범위값을 여러 번 받더라도 2번의 검색과 단순한 연산으로 정답을 얻을 수 있다.
​
이전에 배운 것을 활용하는 것은 좋지만 너무 좁은 '~이것만 사용해야지'~라는 생각을 좀 버리는 것이 좋을 것 같다.
​
좀 멀리 바라보고 생각하는 습관이 필요할 것 같다.