[논문 정리] A Graph-CNN for 3D Point Cloud Classification

0. 포인트 클라우드

여기 의자가 있다.

접이식 철제 의자인 이 물체에 대해 움직여가며 특정 부분에 점을 찍는다고 생각해보자. 표면에도 찍고 손으로는 만질 수 없지만 내부에도 찍을 수 있다면, 이렇게 찍힌 무수히 많은 점들은 결국 접이식 철제 의자의 형상을 나타내며 공간 상에 위치하게 될 것이다.

이렇게 3차원에 존재하는 대상을 여러 개의 점으로 표현한 형태를 포인트 클라우드(point cloud)라 한다.

포인트 클라우드를 구성하는 점들은 각각 3차원 공간 상의 좌표, $(x, y, z)$를 갖는다. 따라서 이 좌표들을 다시 찍어보면 해당 포인트 클라우드가 나타내는 대상을 시각적으로 확인할 수 있다.

지금부터는 레이블이 없는 포인트 클라우드가 주어졌을 때, 그래프 인공 신경망(GNN)을 이용하여
그 포인트 클라우드가 나타내는 대상이 무엇인지 분류하는 모델을 소개한다.

1. Graph Construction

우선 3차원 포인트 클라우드 객체 $X_j$에 대해, 그 레이블을 $y_j$로 가정한다. $X_j$는 $n$개의 점으로 구성되며, $n$개의 점들 각각은 3차원 좌표 $(x, y, z)$를 갖는다.

이러한 점들은 노드로 간주할 수 있다. 이들을 가상의 엣지로 연결하면, 포인트 클라우드로부터 그래프를 생성할 수 있다.

1.1. $k$-NN을 이용한 이웃 관계 생성

포인트 클라우드의 점들에 이웃 관계를 부여하기 위해 $k$-최근접 이웃 알고리즘을 이용한다.
$k$-최근접 이웃 알고리즘은 새로운 대상을 분류하는데 있어 $k$개의 가까운 대상들의 레이블을 활용하는 알고리즘이라고 간략하게 설명할 수 있다.

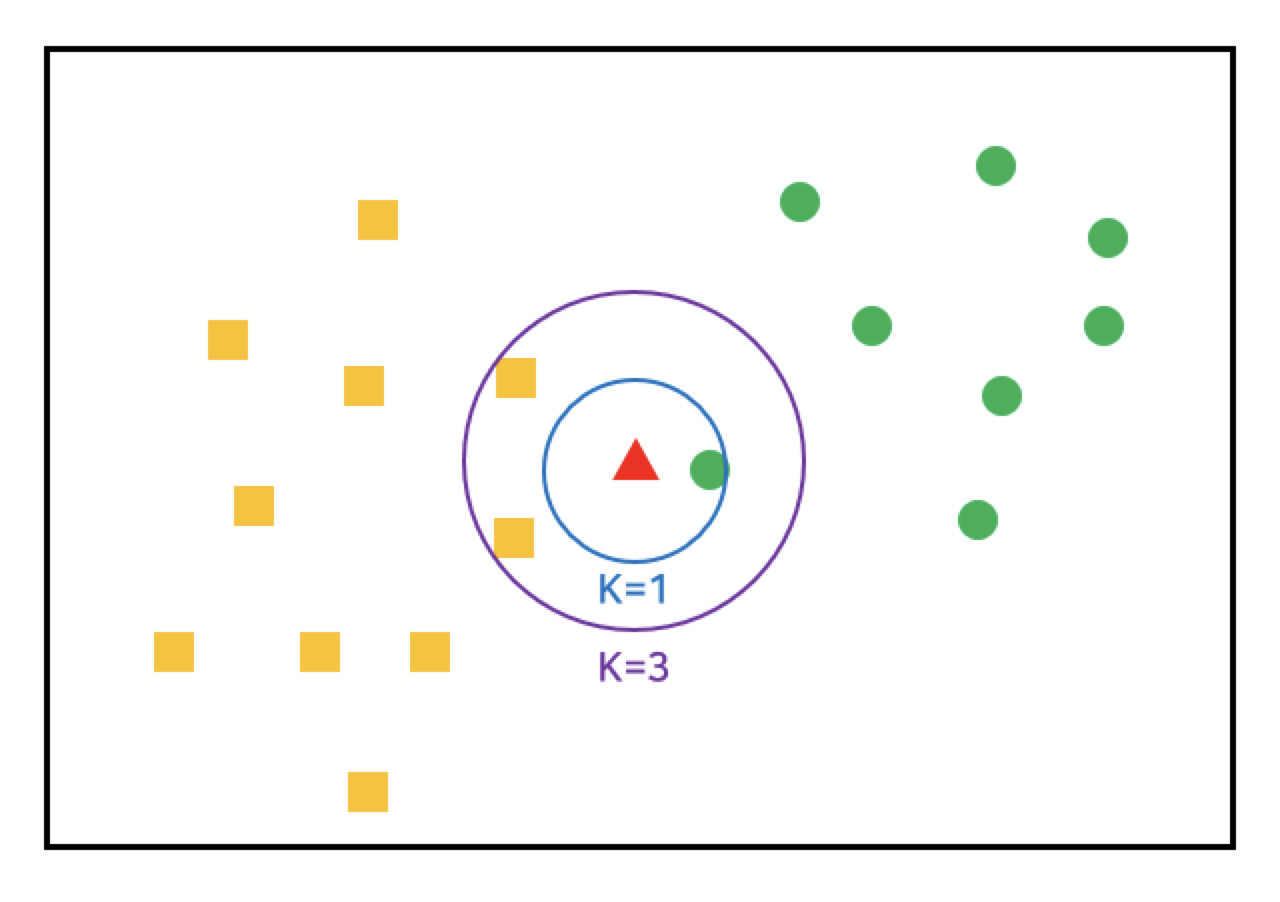
여기서는 각 점들에 대해 유클리드 거리(eucllidean distance)를 기준으로 $k$개의 가까운 점을 탐색하고 그 결과를 해당 점의 이웃으로 가정하는 것으로 $k$NN 알고리즘을 활용한다.

$\mathcal{A}_k(i)$: 점 $i$의 $k$개의 이웃 집합

1.2. 거리에 따라 가중치를 갖는 인접 행렬 생성

위 방식을 통해 점들은 연결되었다. 이러한 연결 관계는 거리를 기준으로 형성되었기 때문에 인접 행렬에도 이러한 정보가 반영되어야 한다. 이에 본 논문에서는 가우시안 커널을 사용한다.

가우시안 커널(Gaussian kernel)은 입력된 두 대상에 대해 거리에 기반하여 유사도를 계산하는 함수로, 식은 아래와 같다.

하이퍼파라미터 $\sigma$: 거리에 따른 유사도 반영 정도

• 너무 크면, 커널의 출력값이 항상 0이 되어 먼 거리에서도 영향을 줄 수 있게 됨.
• 너무 작으면, 거리에 크게 의존하게 되면서 가까운 거리로부터의 영향이 너무 커짐.

이를 사용하여 정의한 가중치 인접 행렬 $W$를 다음과 같이 정의한다.

식에 의하면, 각 점으로부터 $k$NN 알고리즘으로 연결된 이웃 점들에 대해서는 거리에 따른 가중치를 갖고, 연결되지 않은 점들은 0으로 설정된다. 여기서 가중치는 가까울수록 증가하고 멀수록 감소한다.
$(W\in \mathbb{R}^{n\times n})$

$\sigma$의 경우, 본 논문에서는 각 점에서 가장 먼 점까지 거리들의 평균을 사용하였다.

2. Graph Signal Processing

그래프 학습에는 그래프 신호 처리 방법이 사용된다. 신호 처리에서는 시간에 따라 변하는 값인 신호를 그 변화율인 주파수가 형성하는 공간으로 투영하여 해석한다.

비슷한 맥락에서 노드 피처는 노드에 따라 그 값이 변하므로 그래프에서의 신호로 간주할 수 있다.

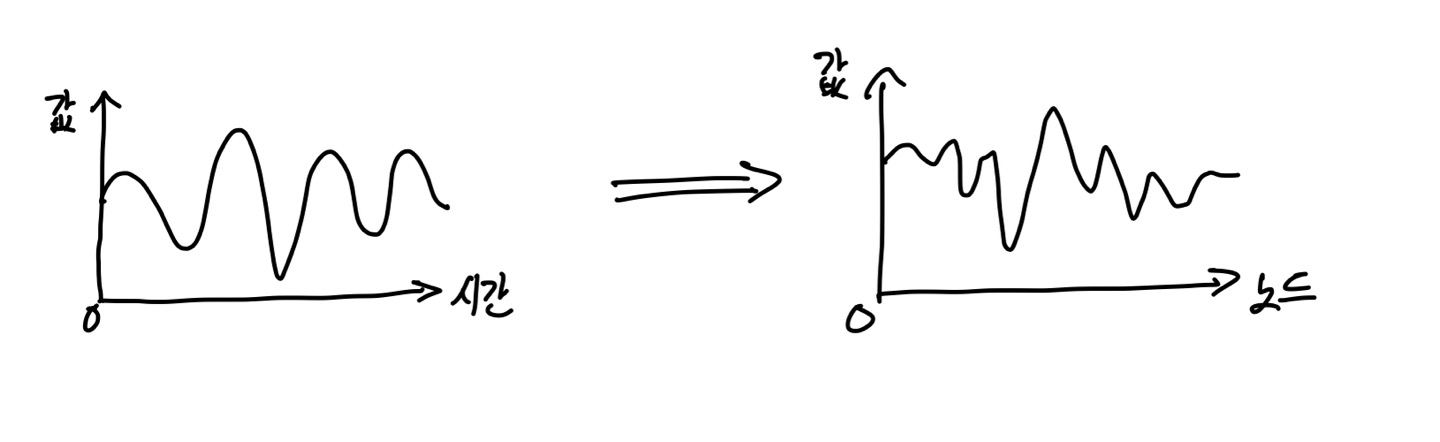
위에서 포인트 클라우드에 $k$-NN 알고리즘을 적용해 생성한 그래프에서는 각 점이 노드가 되며, 각각의 좌표가 해당 노드의 피처로서 존재한다. 따라서 $x$, $y$, $z$ 좌표로 3개의 그래프 신호가 있는 것이다.

신호 처리에서 주파수의 역할은 라플라시안 행렬 $\textbf{\textrm{L}}$이 이어 받는다. 차수 행렬 $\textbf{\textrm{D}}$에서 인접 행렬 $\textbf{\textrm{A}}$을 뺀 형태로 정의되는 라플라시안 행렬에는 노드 피처의 변화량에 대한 정보가 인코딩된다.

이후의 조금 복잡한 과정을 우선 생략하면, 그래프를 학습하는 연산을 아래의 식으로 정리할 수 있다. $h_\alpha$는 그래프 필터로 학습 파라미터 집합을 의미한다.

본 논문에서는 위 식에서 $\textbf{\textrm{L}}^k$ 대신 Chebyshev 다항식을 이용하여 근사하는 방법인 ChebNet을 사용한다.

3. PointGCN

이제부터는 구체적인 모델에 대해 다룬다.

그래프 관점에서 포인트 클라우드를 다루는 PointGCN은 최종 분류 작업을 수행하는 Fully-Connected 레이어 외에 아래의 2가지 레이어로 구성된다.

3.1. Convolutional layer

우선, 입력값은 그래프 신호인 $x$, $y$, $z$ 좌표다. 컨볼루션 연산을 통해 latent feature map을 산출한다.

컨볼루션 연산에는 앞서 설명한 그래프 신호 처리 방법이 사용된다. 이 때 $\textbf{\textrm{L}}$은 입력되는 그래프의 다양성을 고려하기 위해 scaled 라플라시안 행렬 $\tilde{\textbf{\textrm{L}}}=2\textbf{\textrm{L}}/\lambda_{max}-\textbf{\textrm{I}}_n$을 사용한다.

그리고 $\sum_{k=0}^K{\alpha_kT_k(\textbf{\textrm{L}})\textbf{\textrm{x}}}$ 에서 입력되는 $\textbf{\textrm{L}}$과 $\textbf{\textrm{x}}$, 파라미터인 $\alpha$를 제외하면 $K$가 남는다. 여기서 $K$는 이웃의 hop을 의미한다. 즉, 컨볼루션 연산으로 각 노드의 latent feature를 계산할 때 몇 번째 이웃 노드까지 연산에 포함시킬지가 되며, 하이퍼파라미터에 해당한다.

컨볼루션 레이어는 ReLu를 거친 연산 결과를 출력한다.

3.2. Pooling layer

풀링 레이어에서는 노드 수만큼 존재하는 latent representation의 차원을 줄여 정보를 압축한다. 이를 위해 본 논문에서는 2가지 방법을 제안한다.

Global pooling
간단하게 데이터의 통계적 정보를 이용하는 방법이다. 여기서는 latent feature마다 최댓값만을 가져오는 1-max pooling과 분산을 계산하여 사용하는 variance pooling이 사용될 수 있다.

2가지 모두 latent representation의 순서와 무관한 값을 출력하고, 한 번의 풀링으로 $n$차원을 1차원으로 압축한다.

Multi-resolution pooling
먼저 한 점을 뽑고, 다시 그 점에서 가장 거리가 먼 점을 뽑는다. 그 다음부터는 앞서 뽑힌 점들과 가장 먼 점을 단계적으로 뽑아나간다. 일정 수만큼 샘플링한 후에는, 뽑히지 않은 점들을 뽑힌 점들 중 가장 가까운 점으로 군집화한다. 생성된 군집들에 대해서 다시 최댓값을 추출하여 풀링을 마무리한다.

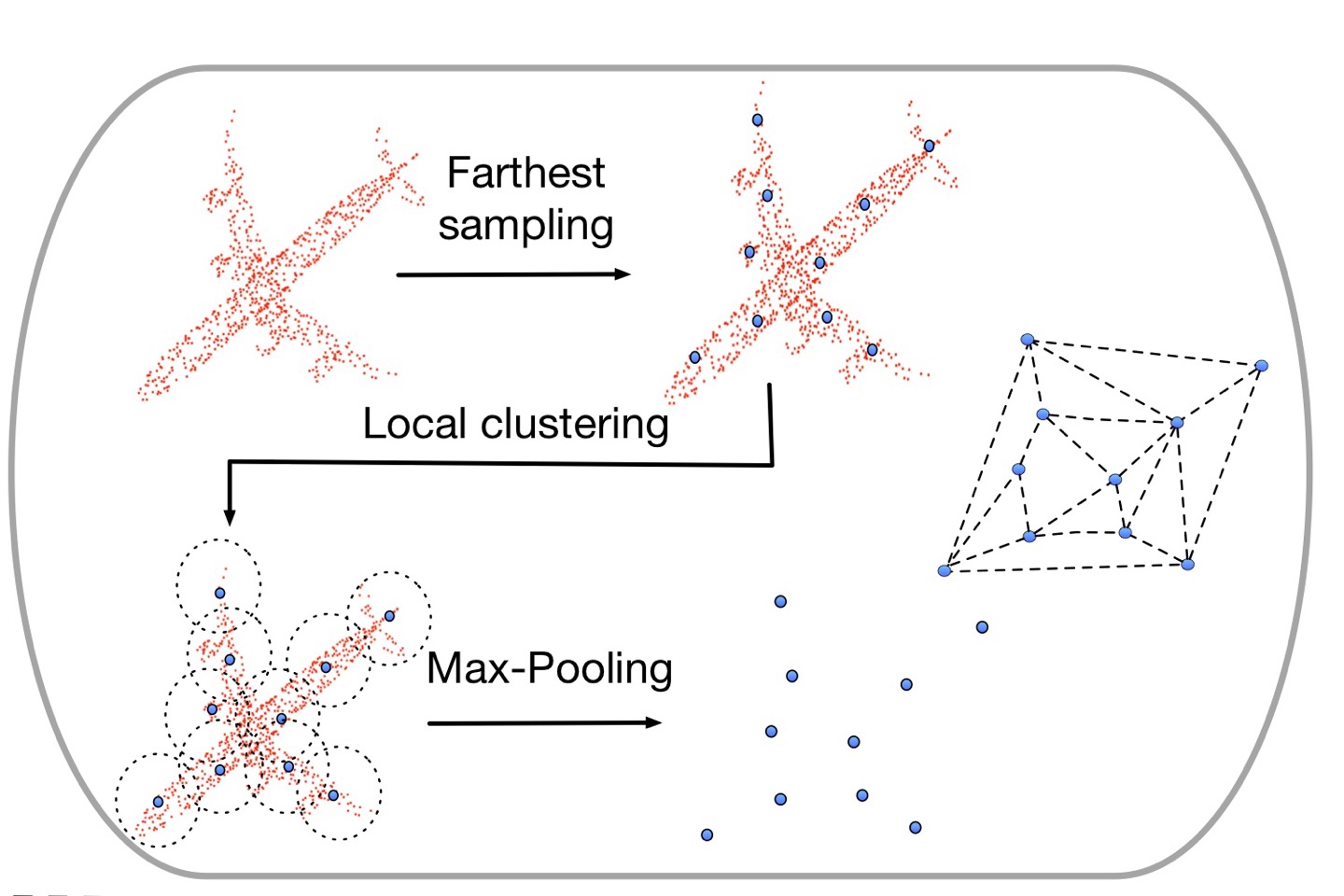
이 방법은 한 번의 풀링으로 1차원으로 압축되지 않기 때문에 Fully-Connected 레이어에 입력되기 전에 글로벌 풀링 방법이 수반된다.

3.3. Final Architecture

모델의 최종 아키텍처는 아래의 그림으로 나타낼 수 있다. 어떤 방법을 이용하여 풀링을 진행하는지에 따라서 2개의 다른 모델로 구분할 수 있다.

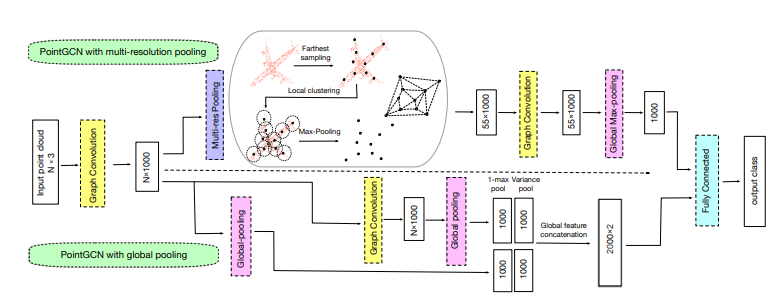
초기에 입력되는 값은 N개의 점의 3차원 좌표(N×3)이다. 이를 1000개의 필터를 통해 latent feature map(N×1000)을 산출한다. Latent feature map은 풀링으로 차원이 축소되며(55 or 1 ×1000) 분류를 위한 레이어에 입력된다.

4. Experiments

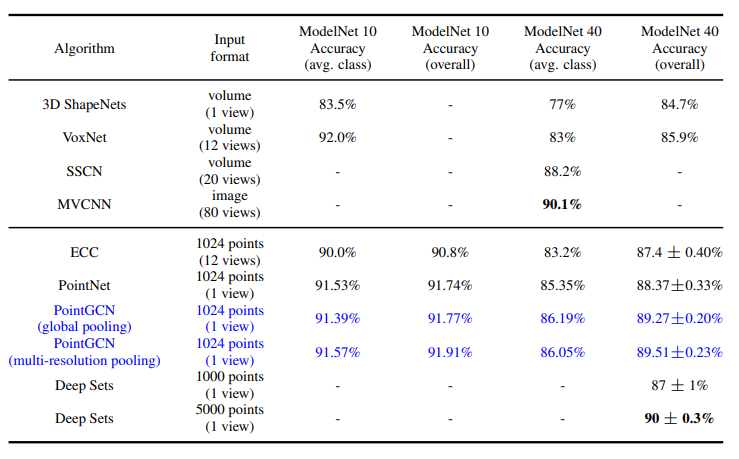
실험은 3차원 물체 인식을 위한 데이터셋인 ModelNet40과 ModelNet10에 대해 수행되었다. 논문에서는 아래와 같이 다른 모델과의 비교 실험 결과를 제시한다.

개인적으로 인상적이었던 점은 실험 결과보다 풀링의 영향이었다. 아래 그림에는 레이어마다 max pooling을 통해 추출된 점이 나타나 있다.

왼쪽이 원래 기타를 표현한 포인트 클라우드다. 중간과 오른쪽은 각각 레이어를 1번, 2번 거쳐 max pooling된 점들을 나타낸 것이다. Max pooling은 간단한 방법이지만 2번 거친 결과를 보면 얼추 기타를 유추할 수 있을 정도로 충분한 성능을 보여주는 것을 확인할 수 있었다.