[BOJ 9251, 9252] LCS

kiraMe·2025년 5월 13일

Algorithm

목록 보기

4/11

LCS (Longest Common Subsequence)

: 두 수열이 주어졌을 때 Subsequence 중 가장 긴 것을 찾는 문제

⚠️ Subsequence와 Substring을 혼동하면 안 된다.

✅ Substring이란? 공통된 문자가 연속적으로 존재하는 문자열
ABCDE의 Substring: A, ABC, BCDE, …
ABCDE와 ACEDE의 LCS(ubstring): DE

☑️ Subsequence란? 모두의 부분 수열이 되는 수열
ABCED의 Subsequence: A, ACE, BED, ABCD… (단, ACB와 같은 문자열은 불가)
ABCED와 ACEDE의 LCS(ubsequence): ACED

그럼 Longest Common Subsequence는 어떻게 구할까?

Longest Common Substring 문제를 먼저 해결해보면 이해하기 쉽다.

✅ Largest Common Substring

: 공통된 문자열 중 가장 긴 것(또는 그 길이)을 찾는 문제

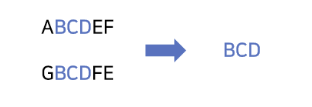
→ String1과 String2를 비교하면서
문자가 같으면 cnt++
문자가 다르면 cnt=0부터 다시 센다!

ABCDEF와 GBCDFE를 비교해보자!

계산의 편의를 위해 [0][0]은 0으로 설정해두고 시작한다.
G와 ABCDEF를 차례대로 비교한다. (겹치는, 즉, 같은 문자 없으므로 모두 0)
B와 ABCDEF를 차례대로 비교한다. (같은 문자일 경우 cnt++)
같은 방법으로E와 ABCDEF까지 비교한다.
탐색이 끝난 후 최장 거리를 찾으면 끝.

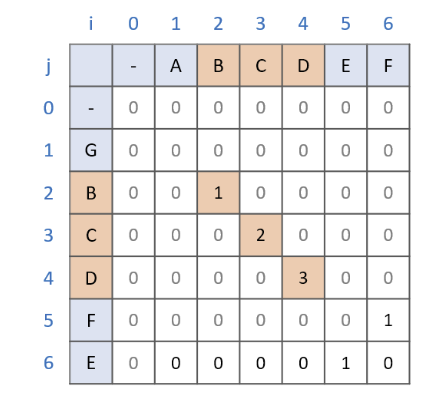
그래서 Largest Common Substring을 왜 구했냐?

Largest Common Subsequence와 다른 점이 딱 하나 있기 때문이다.

Subsequence는 연속될 필요가 없다!

따라서 비교 문자가 서로 다를 때 cnt가 0으로 초기화되지 않고 이전 값으로 유지된다.

이때 이전 값은 최장 길이를 구해야 하므로, 당연히 가장 큰 값이 계속되어야 한다.

그럼 이제 진짜로 Largest Common Subsequence를 구해보자.

☑️ Largest Common Subsequence

: 공통된 Subsequence 중 가장 긴 것(또는 그 길이)을 찾는 문제

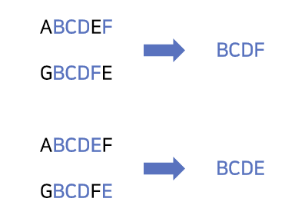
→ String1과 String2를 비교하면서

문자가 같으면 cnt++

dp[i-1][j-1] + 1

문자가 다르면 cnt = 이전 값 중 가장 큰 값

max([i][j-1], [i-1][j])

ABCDEF와 GBCDFE를 비교해보자!

계산의 편의를 위해 [0][0]은 0으로 설정해두고 시작한다.
G와 ABCDEF를 차례대로 비교한다. (겹치는, 즉, 같은 문자 없으므로 모두 이전 값 중 최댓값을 유지) max([i][j-1], [i-1][j])
B와 ABCDEF를 차례대로 비교한다. (같은 문자일 경우 cnt++) dp[i-1][j-1] + 1
같은 방법으로 E와 ABCDEF까지 비교를 완료한다.
탐색이 끝난 후 최장 거리를 찾으면 끝.

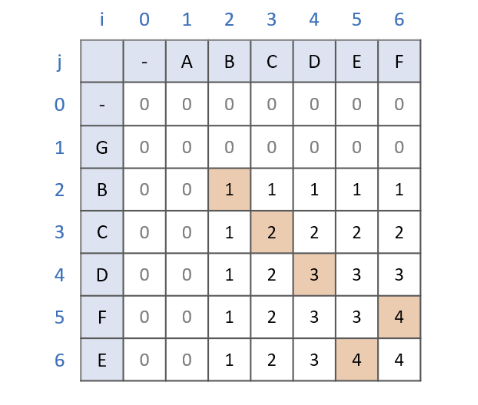
이때 LCS 문자열을 찾고 싶다면?

단순히 cnt(최장 거리)를 구하고 싶은게 아니라 문자열 자체를 알고 싶다면,

우선 같은 방법으로 탐색을 해 LCS배열(dp)을 완성한 후
배열의 마지막에서 시작해, 다음 방법으로 탐색을 한다.
1. dp[i-1][j]와 dp[i][j-1] 중 같은 값을 찾아간다
2. 같은 값이 없다면 result에 추가하고 dp[i-1][j-1]을 찾아간다
3. 값이 0이면 종료한다
result 배열을 거꾸로 뒤집으면 끝.

구현 코드

# BOJ 9251 (https://www.acmicpc.net/problem/9251)
# LCS(Longest Common Subsequence, 최장 공통 부분 수열)문제는 두 수열이 주어졌을 때, 
# 모두의 부분 수열이 되는 수열 중 가장 긴 것을 찾는 문제이다.
# 예를 들어, ACAYKP와 CAPCAK의 LCS는 ACAK가 된다.
# 입력 # 첫째 줄과 둘째 줄에 두 문자열이 주어진다. 문자열은 알파벳 대문자로만 이루어져 있으며, 최대 1000글자로 이루어져 있다.
# 출력 # 첫째 줄에 입력으로 주어진 두 문자열의 LCS의 길이를 출력한다.
# 예제 입력 1
# ACAYKP
# CAPCAK
# 예제 출력 1 
# 4
# ------------------------------------------------------------

class Solution:

    def LCS(str1, str2):

        L1 = len(str1)+1
        L2 = len(str2)+1

        dp = [[0 for _ in range(L2)] for _ in range(L1)] ### 2차원 배열 생성 시 주의

        for i in range(1, L1):
            for j in range(1, L2):
                dp[i][j] = dp[i-1][j-1] + 1 if str1[i-1] == str2[j-1] else max(dp[i-1][j], dp[i][j-1])
                
        return dp[L1-1][L2-1]
    
str1 = input().strip()
str2 = input().strip()
ans = Solution.LCS(str1, str2)
print(ans)

# BOJ 9252 (https://www.acmicpc.net/problem/9252)
# LCS 2
# LCS 길이와 LCS 배열까지 같이 구하기

str1 = input()
str2 = input()

L1 = len(str1) + 1
L2 = len(str2) + 1

dp = [ [ 0 for _ in range(L2) ] for _ in range(L1) ]

for i in range(1, L1):
    for j in range(1, L2):

        if str1[i-1] == str2[j-1]:
            dp[i][j] = dp[i-1][j-1] + 1
        
        else: # !=
            # sequentially count
            dp[i][j] = max(dp[i-1][j], dp[i][j-1])


LCS = ""
i = L1 - 1
j = L2 - 1
count = dp[i][j]

while dp[i][j] > 0:
    
    if dp[i][j] == dp[i-1][j]:
        i -= 1

    elif dp[i][j] == dp[i][j-1]:
        j -= 1

    else:
        LCS += str1[i-1]
        i -= 1
        j -= 1
    
print(count)
if count > 0:
    print("".join(reversed(list(LCS)))) 

# Self-feedback
# 너무 외워져 있음
# 시간이 좀 흐른 후에 다시 풀어보기