큐 Queue
자료를 보관할 수 있는 (선형)구조
단, 넣을때는 한쪽 끝에서 밀어 넣어야 하고(인큐 ebqueue) 꺼낼때에는 반대쪽에서 뽑아 꺼내야 함(디큐 dequeue)
- 선입선출(FIFO) : 들어간 순서와 동일한 순서로 꺼내짐
큐의 동작
- 초기 상태 : empty queue
Q = Queue()
| [Q] |
|---|
| - |
| - |
| - |
- 데이터 원소 A를 큐에 추가
Q.enqueue(A)
Q.enqueue(B)
| [Q] |
|---|
| - |
| B |
| A |
- 데이터 원소 꺼내기
r1 = Q.dequeue() → A
| [Q] |
|---|
| - |
| - |
| B |
r2 = Q.dequeue() → B
| [Q] |
|---|
| - |
| - |
| - |
큐의 추상적 자료구조 구현
- array를 이용하여 구현 → python 리스트와 메서드 이용
- linked list를 이용하여 구현 → 양방향 연결리스트 이용
연산의 정의
- size() : 현재 큐에 들어있는 데이터 원소의 수
- isEmpty() : 현재 큐가 비어있는지 판단
- enqueue(x) : 데이터 원소 x를 큐에 추가
- dequeue() : 큐의 맨 앞에 저장된 데이터 원소 제거 and 반환
- peek() : 큐의 맨 앞에 저장된 데이터 원소 반환
배열로 구현한 큐
- 빈 큐를 초기화
class ArrayQueue:
def __init__(self):
self.data = []- 큐의 크기를 리턴하고 큐가 비어있는지 판단
def size(self):
return len(self.data)
def isEmpty(self):
return self.size() == 0- 데이터 원소 추가 (= 스택의 push연산)
def enqueue(self.item):
self.data.append(item)- 데이터 원소 삭제(리턴)
def dequeue(self):
return self.data.pop(0) # 0번 인덱스 리턴- 큐의 맨 앞 원소 반환
def peek(self):
return self.data[0]배열로 구현한 큐의 연산 복잡도
| 연산 | 복잡도 |
|---|---|
| size( ) | O(1) |
| isEmpty( ) | O(1) |
| enqueue( ) | O(1) |
| dequeue( ) | O(n) |
| peek( ) | O(1) |
dequeue( )의 시간복잡도가 O(n)인 이유
| 20 | 37 | 58 | 65 | 72 | 91 |
|---|
맨 앞에 있는 20을 꺼내려고 할 때,
| 37 | 58 | 65 | 72 | 91 | - |
|---|
원소를 하나하나 당겨야 해서 배열의 길이가 길면 오래걸림
환형 큐 Circular Queue
정해진 개수의 저장 공간을 빙 돌려가며 이용
→ front와 rear을 적절히 계산하여 배열을 환형으로 재활용
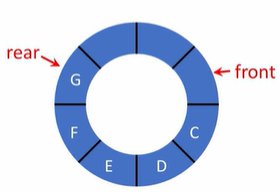 rear : 데이터를 집어넣는 쪽
rear : 데이터를 집어넣는 쪽
front : 데이터를 꺼내는 쪽
- 큐가 가득 차면 더이상 원소를 넣을 수 없기 때문에 큐 길이 기억하고 있어야됨
연산의 정의
- size() : 현재 큐에 들어있는 데이터 원소의 수
- isEmpty() : 현재 큐가 비어있는지 판단
- isFull() : 큐에 데이터 원소가 꽉 차있는지 판단
- enqueue(x) : 데이터 원소 x를 큐에 추가
- dequeue() : 큐의 맨 앞에 저장된 데이터 원소 제거 and 반환
- peek() : 큐의 맨 앞에 저장된 데이터 원소 반환
배열로 구현한 환형 큐
길이 n = 6인 리스트 확보
| - | - | - | - | - | - |
|---|
Q.enqueue(A)
| A | - | - | - | - | - |
|---|---|---|---|---|---|
| rear | - | - | - | - | - |
Q.enqueue(B)
| A | B | - | - | - | - |
|---|---|---|---|---|---|
| - | rear | - | - | - | - |
Q.enqueu(C)
| A | B | C | - | - | - |
|---|---|---|---|---|---|
| - | - | rear | - | - | - |
Q.enqueue(D)
| A | B | C | D | - | - |
|---|---|---|---|---|---|
| - | - | - | rear | - | - |
r1 = Q.dequeue( ) → A
| B | C | D | - | - | |
|---|---|---|---|---|---|
| front | - | - | rear | - | - |
r2 = Q.dequeue( ) → B
| C | D | - | - | ||
|---|---|---|---|---|---|
| - | front | - | rear | - | - |
Q.enqueue(E)
| C | D | E | - | ||
|---|---|---|---|---|---|
| - | front | - | - | rear | - |
Q.enqueue(F)
| C | D | E | F | ||
|---|---|---|---|---|---|
| - | front | - | - | - | rear |
Q.enqueue(G) 이때, 환형 큐이기 때문에 rear가 다시 처음으로 돌아감
| G | C | D | E | F | |
|---|---|---|---|---|---|
| rear | - | front | - | - | - |
r3 = Q.dequeue( ) → C
| G | D | E | F | ||
|---|---|---|---|---|---|
| rear | - | front | - | - | - |
배열로 구현한 환형 큐
- 빈 큐를 초기화 → 인자로 주어진 최대 큐 길이 설정
class CircularQueue:
def __init__(self,n):
self.maxCount = n
self.data = [None] * n
self.count = 0
self.front = -1
self.rear = -1- 현재 큐 길이 반환
def size(self):
return self.count- 큐가 비어있는지 꽉 차 있는지 판단
def isEmpty(self):
return self.count == 0
def isFull(self):
return self.count == self.maxCount- 큐에 데이터 원소 추가
def enqueue(self, x):
if self.isFull():
raise IndexError('Queue full')
self.rear = (self.rear + 1) % self.maxCount
self.data[self.rear] = x
self.count += 1- 큐에서 데이터 원소 뽑아내기
def dequeue(self):
if self.isEmpty():
raise indexError('Queue empty')
self.front = (self.front + 1) % self.maxCount
x = self.data[self.front]
self.count -= 1
return x- 큐의 맨 앞 원소 들여다보기
def peek(self):
if self.isEmpty:
raise IndexError('Queue empty')
return self.data[(self.front + 1) % self.maxCount]우선순위 큐 Priority Queues
큐가 FIFO방식을 따르지 않고 원소들의 우선순위에 따라 큐에서 빠져나오는 방식
우선순위 큐의 구현
- 방식 선택
- enqueue할때 우선순위 순서를 유지하도록
- dequeue할때 우선순위 높은 것을 선택
→ 1번이 더 유리. 2번은 모든 데이터들을 하나하나 살펴봐야 하기때문에 큐의 길이에 비례하는 시간이 걸림
- 자료구조 선택
- 선형 배열 이용
- 연결 리스트 이용
→ 시간적으로 볼때는 연결리스트가 더 유리 but 선형 배열이 메모리 덜 소요
양방향 연결 리스트를 이용하여 구현한 우선순위 큐
- 빈 큐를 초기화
from doublylinkedlist import Node, DoublyLinkedList
class PriorityQueue:
def __init__(self,x):
self.queue = DoublyLinkedList()- enqueue
이때, 양방향 연결 리스트의 getAt( )메서드 이용 X
def enqueue(self,x):
newNode = Node(x)
curr = self.queue.head
while curr.next != self.queue.tail and x < curr.next.data:
curr = curr.next
self.queue.insertAfter(curr, newNode)- dequeue
def dequeue(self):
return self.queue.popAt(self.queue.getLength())- peek
def peek(self):
return self.queue.getAt(self.queue.getLength()).data
