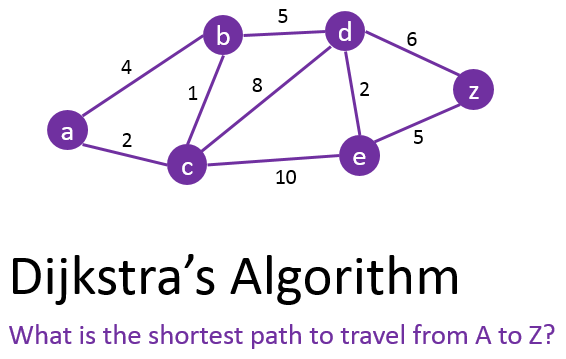
dijkstra algorithm

• 다익스트라 알고리즘은 shortest path중 'Start Vertex' -> 'Dst Vertex' 이기 때문에
  항상 Start dist 리스트를 중점적으로 생각한다.!!!
• 다익스트라 알고리즘에서는 가중치가 음수이면 안된다!! 0＜ 가중치 이어야한다.

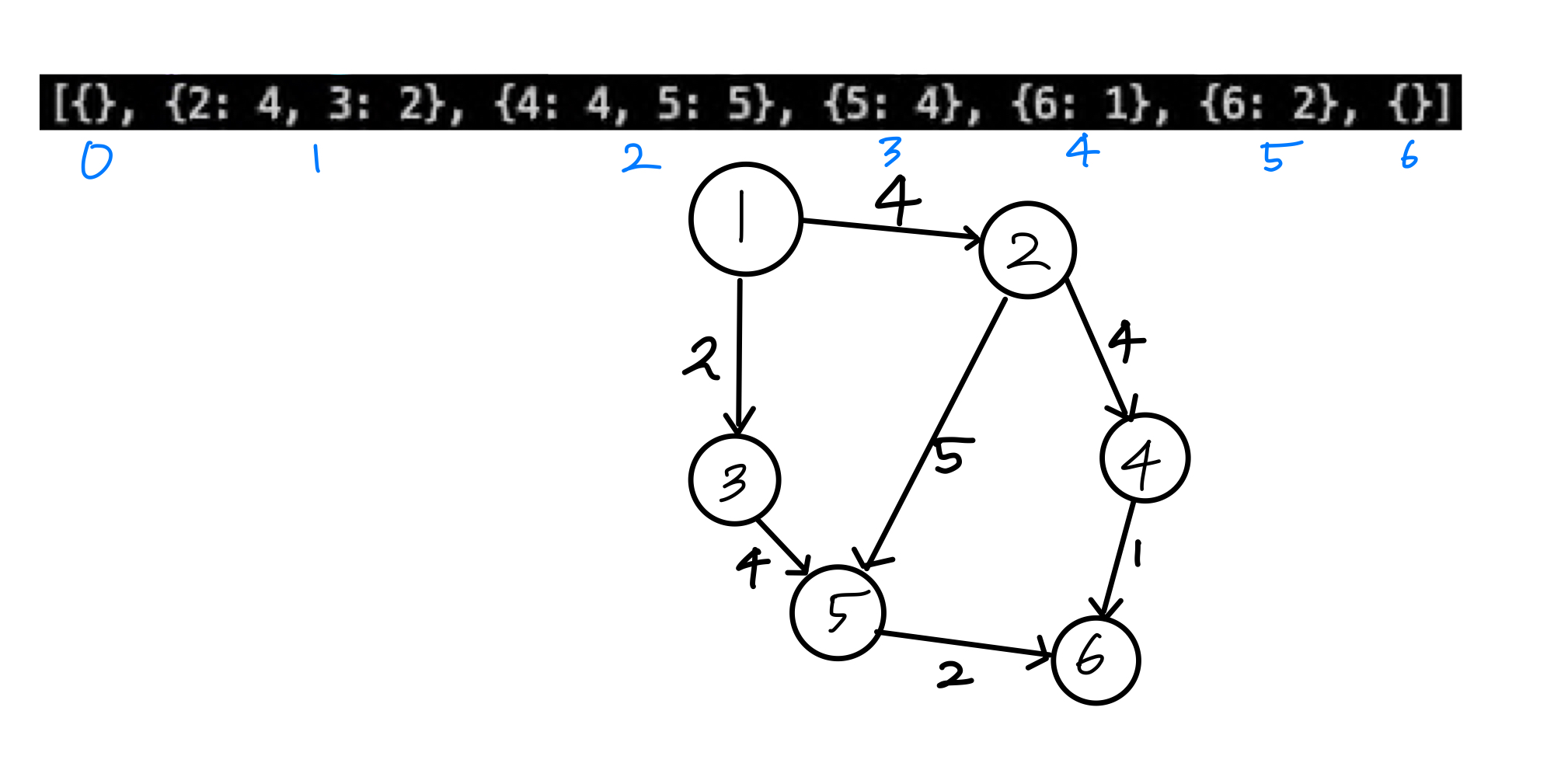
• 아래와 같이 N개의 Vertex와 E개의 Edge가 차례대로 입력이된다.
  • V1 V2 value라고 한다.

6 7
1 2 4
1 3 2
2 4 4
2 5 5
3 5 4
4 6 1
5 6 2

• 본인이 편한 방식대로 graph 리스트를 만들자.
  • maps 라는 그래프를 가지는 dict를 만듦
  • 편의상 1번 vertex부터 유의미한 데이터를 넣음

import sys

readl=sys.stdin.readline
V,E=map(int,readl().strip().split())
maps=[ dict() for _ in range(V+1) ]
for i in range(0,E):
    V1, V2, cost=map(int, readl().strip().split())
    maps[V1].update({V2:cost})


print(*maps,sep='\n') # "[{}, {2: 4, 3: 2}, {4: 4, 5: 5}, {5: 4}, {6: 1}, {6: 5}, {}]

• dist 라는 start 입장에서 본, 가중치를 담은 리스트를 만든다.
  • 기본 값으로 float('inf')를 넣는다.
    • start 의 dist만! 0으로 넣는다.
      dist[start] = 0

dist=[float('inf')]*(V+1)
start=1 # 시작 버텍스 번호

dist[start]=0 # start vertex에서 자기 자신을 방문하는 Edge는 없으니까..
print(dist)  # [inf,0,inf,inf,inf,inf,inf]

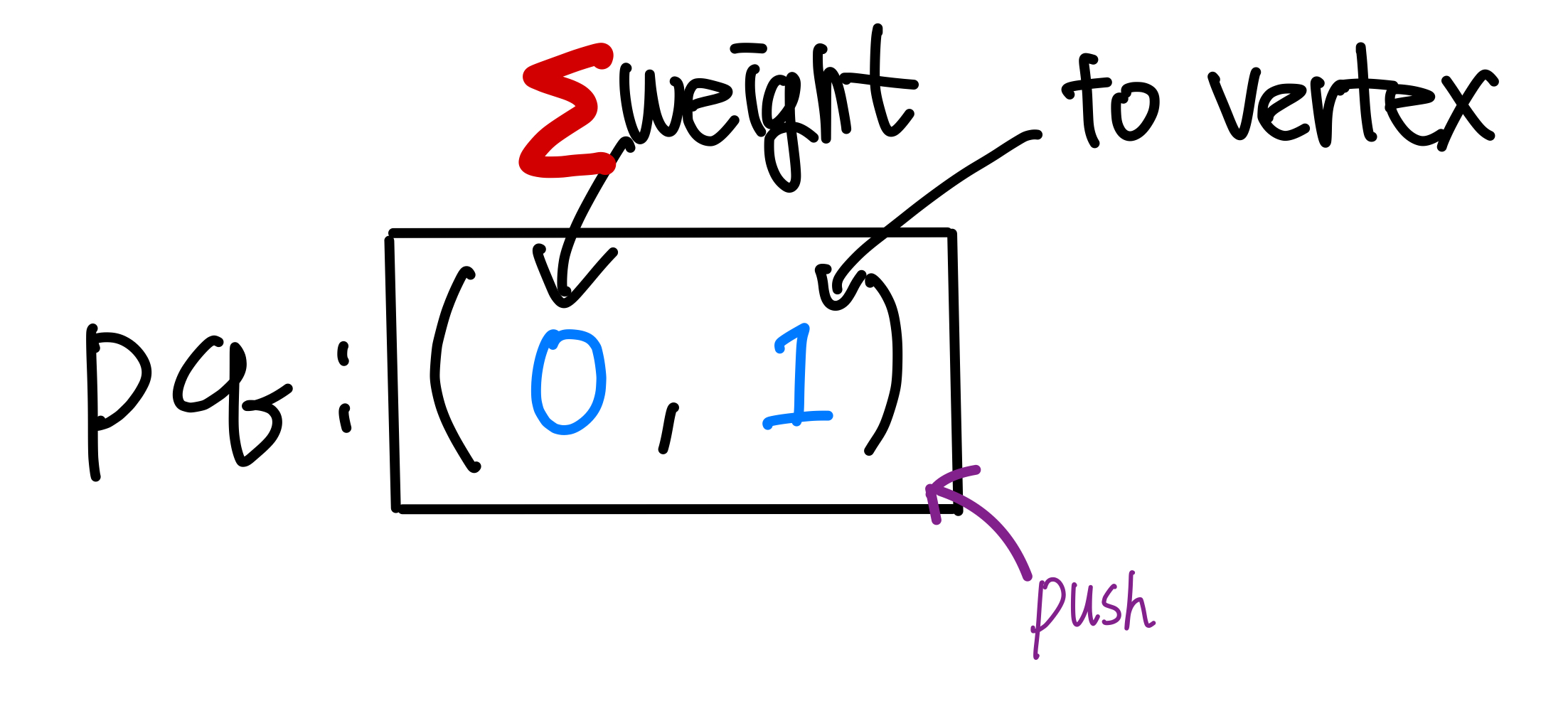
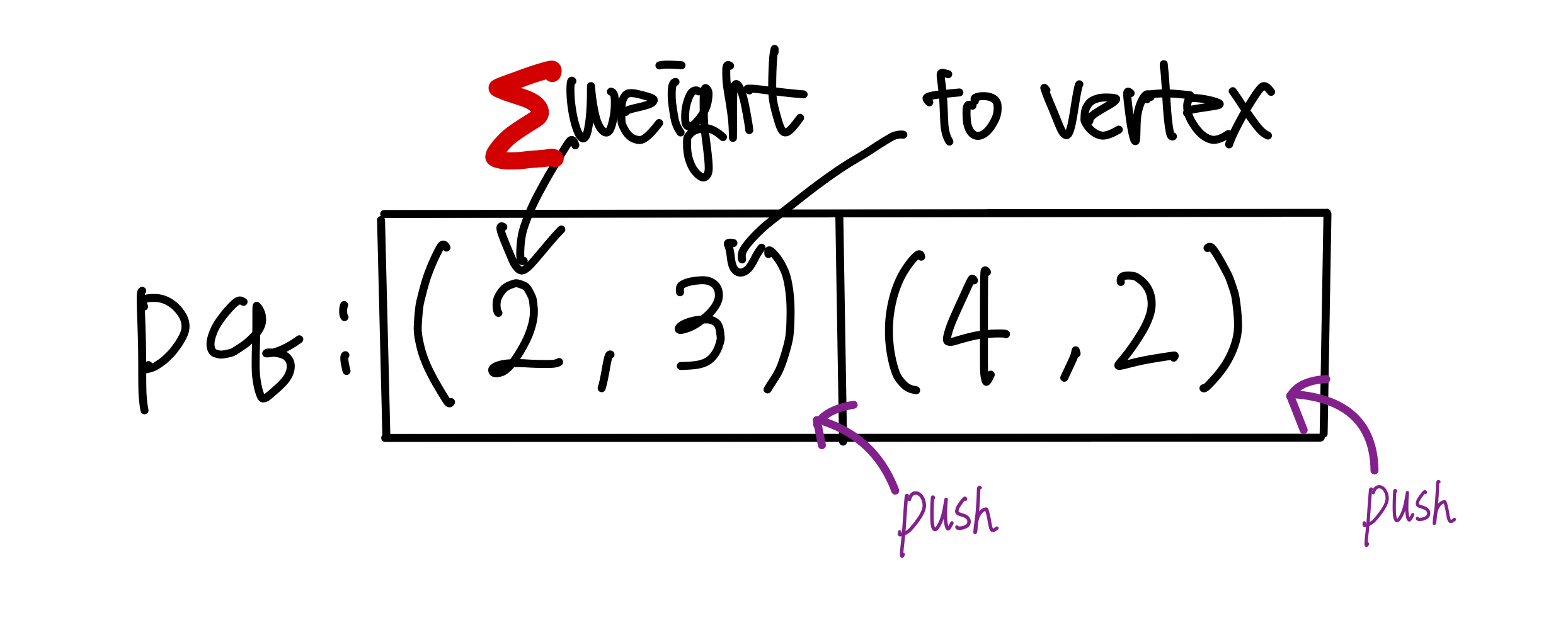
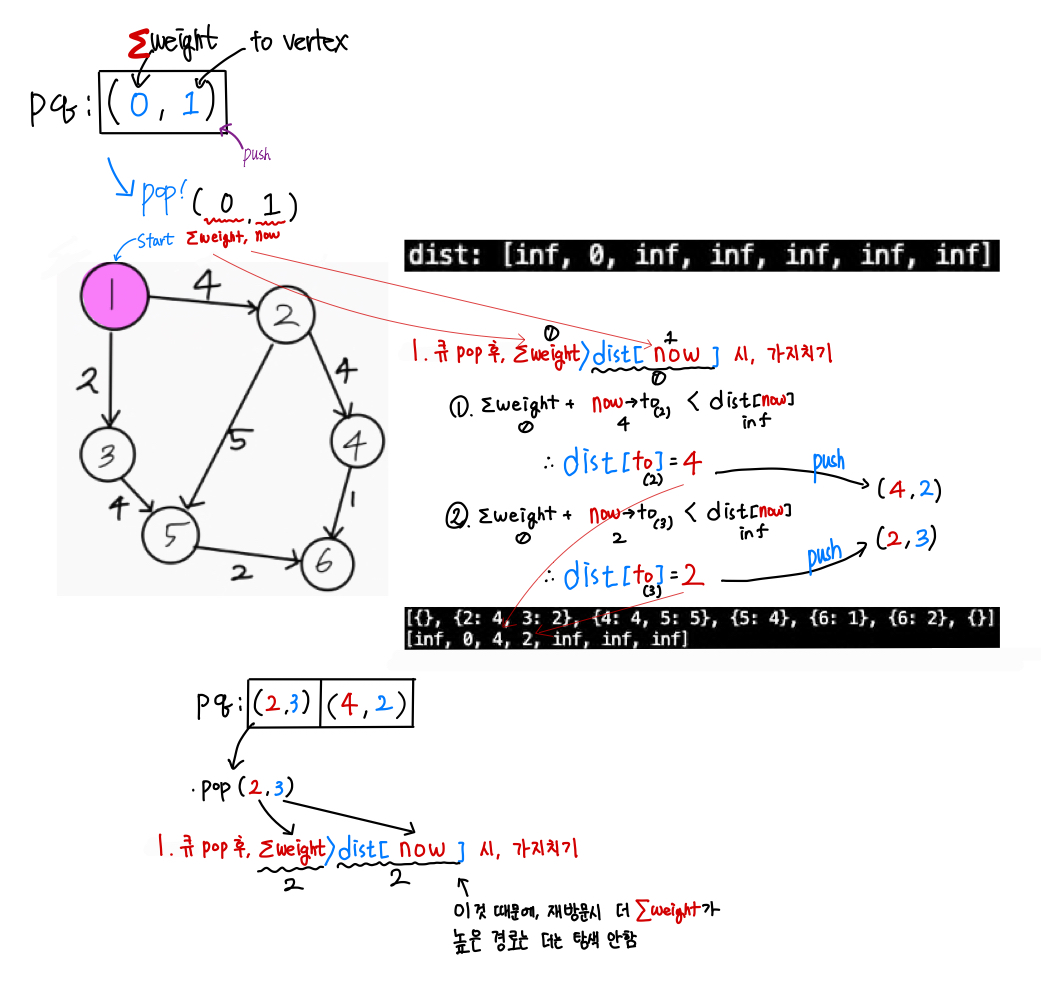
• priority queue 를 만들고, 내용은 ($∑weight$, vertex) 로 한다.
  • 우선 순위 큐에서 $∑weight$ 가 낮은 순으로 min heap 정렬한다.

• ★ 첫 번째로, start -> to 로 가는 내용을 큐에 담는다. ★

pq=[]
heapq.heappush(pq, ( dist[start] , start ) )

while pq:
    sig_weight, now = heapq.heappop(pq)
    if dist[now] < sig_weight: continue # ∑weight 가 dist[now] 보다 크면, 탐색할 필요가 없다.
    for to in maps[now].keys():
        if sig_weight + maps[now][to] < dist[to]:
            dist[to]=sig_weight+maps[now][to]
            heapq.heappush(pq, ( dist[to] , to ) )
            #heapq.heappush(pq, ( sig_weight+maps[now][to] , to ) ) # 위와 같은 문장임
            # 첫 큐 실행 시,       ( 0 + 4 , 2 )
            # 첫 큐 실행 시,       ( 0 + 2 , 3 )
            

import sys
import heapq

if __name__ == '__main__':
    readl=sys.stdin.readline
    V,E=map(int,readl().strip().split())
    # create map graph
    maps=[ dict() for _ in range(V+1) ]
    for i in range(0,E):
        V1, V2, cost=map(int, readl().strip().split())
        maps[V1].update({V2:cost})

    start=1

    # create dist list
    dist=[float('inf')]*(V+1)

    dist[start]=0
    
    print(f'dist: {dist}') 
    pq=[]
    heapq.heappush(pq,(dist[start],start))
                    # (weight, to)

    while pq:
        sig_weight, now = heapq.heappop(pq)
        if sig_weight > dist[now]: continue
        for to in maps[now].keys():
            if sig_weight+maps[now][to] < dist[to]:
                dist[to]=sig_weight+maps[now][to]
                heapq.heappush(pq,(dist[to],to))
    print(f'dist: {dist}')