[백준] 9251번: LCS

9251번

문제

LCS(Longest Common Subsequence, 최장 공통 부분 수열)문제는 두 수열이 주어졌을 때, 모두의 부분 수열이 되는 수열 중 가장 긴 것을 찾는 문제이다.

예를 들어, ACAYKP와 CAPCAK의 LCS는 ACAK가 된다.

어떻게 풀면 좋을까?

DP 문제다. 점화식을 세워서 풀어야 한다. DP... 정말 쥐약이다.
LCS 풀이
영상에서 상세하게 설명해준다.

풀이

ACAYKP와 CAPCAK

공통 부 문자열을 구해보자.

X = A C A Y K P
Y = C A P C A K

공통 부 문자열 (숫자는 공통 문자열의 길이)

1
A, C, K, P

2
AC, AA, AK, AP, CA, CK, CP

3
ACA, ACK, AAK, CAK, CAP

4
ACAK

5
없다.

ACAYKP를 Xn
CAPCAK를 Ym 이라고 보자.

Xn = x1 x2 x3 x4 .... xn   =>   X6 = x1 x2 x3 x4 x5 x6
Ym = y1 y2 y3 y4 .... ym   =>   Y6 = y1 y2 y3 y4 y5 y6

위에는 n와 m이 같은 예제인데,
n과 m은 같을수도 있고, 다를수도 있다. 즉 문자열의 길이는 같을수도, 다를수도 있다.

결국 우리가 구하고자 하는 식은
**LCS(Xn, Ym)** 이다. 그리고 이는 Xn, Ym의 공통 부 문자열의 길이다.

그리고 이를 다시 부 문제로 표현하면,

**LCS(i, j)** 즉, Xi와 Yj의 LCS의 길이를 구하는 문제이다. i 가 n일 때, j가 m일 때의 값이다.
이는 다시 다음과 같이 표현된다.
Xi = x1 x2 x3 ... xi
Yj = y1 y2 y3 ... yj

마지막 문자부터 살펴보자. xi 와 yj 문자는 두 문자가 **같은 경우**와 **다른 경우**가 있을 것이다.
예제에서는 P와 K를 본건데 둘은 다른 경우겠다.

먼저 **같은 경우**를 보자.
xi와 yj가 같다는 말은... 예를 들면

x1 x2 x3 ... B
y1 y2 y3 ... B 가 되겠다.

마지막 문자가 같다는 것은 마지막 두 문자가 LCS(i,j)에 포함 된다는 것이다.

A C D B
A D D B 하면 A D B 가 최장 길이다 되듯이, 마지막 두 문자는 결과물에 포함이 된다.

즉, 앞의 결과가 어떻든 간에 길이가 1 추가된다는 것이다.
이를 점화식으로 표현하면

**LCS(i, j) = LCS(i-1, j-1) + 1

(A C D)** B => 여기서 A D 뽑고
**(A D D)** B => 여기서 A D 뽑은 다음 마지막 B를 추가!

이번엔 마지막 문자가 **다른 경우**를 살펴보자.
Xi: **A** **B** **C** D **A**
Yj: **A** **B** **C** **A** B

여기서 최장은 A B C A
Xi의 마지막 A가 정답에 포함된 경우다.    ==> 경우의 수 1
이 때 Yj의 B는 절대 뽑히지 않는다.

반대로 Yj의 마지막 문자가 뽑힌다면? 예제가 이 경우다.
Xi = A C A Y K P
Yj = C A P C A K
A C A K 로 K가 마지막에 포함 되었다.   ==> 경우의 수 2
이 떄 Xi의 P는 절대 뽑히지 않는다.

즉, 마지막 문자가 다른경우에는 둘 다 뽑히는 경우는 절대로 없다.
**하나만 뽑히거나**, **아예 안 뽑히거나** 이다.

아예 뽑히지 않으려면
A B C F
A B C E 같은 경우가 있으려나?

경우의 수 1
**Xi**의 마지막 문자가 뽑혔을 경우에는
**Xi**의 **모든 문자**와 **Yj**에서 **마지막 문자를 뺀 문자**에서의 LCS를 구하면된다.

이를 점화식으로 표현하면
LCS(i, j-1)

=============================================================================

경우의 수 2
**Yj**의 마지막 문자가 뽑혔을 경우에는
**Yj**의 **모든 문자**와 **Xi**에서 **마지막 문제를 뺀 문자**에서의 LCS를 구하면된다.

이를 점화식으로 표현하면
LCS(i-1, j)

그리고 우리가 구하는건 최장의 LCS길이다.
max(LCS(i, j-1), LCS(i-1, j))를 구한다.

...하..

표는 .. 스크린샷으로 따왔다.
영상에서 
X = A B C B D A B
Y = B D C A B A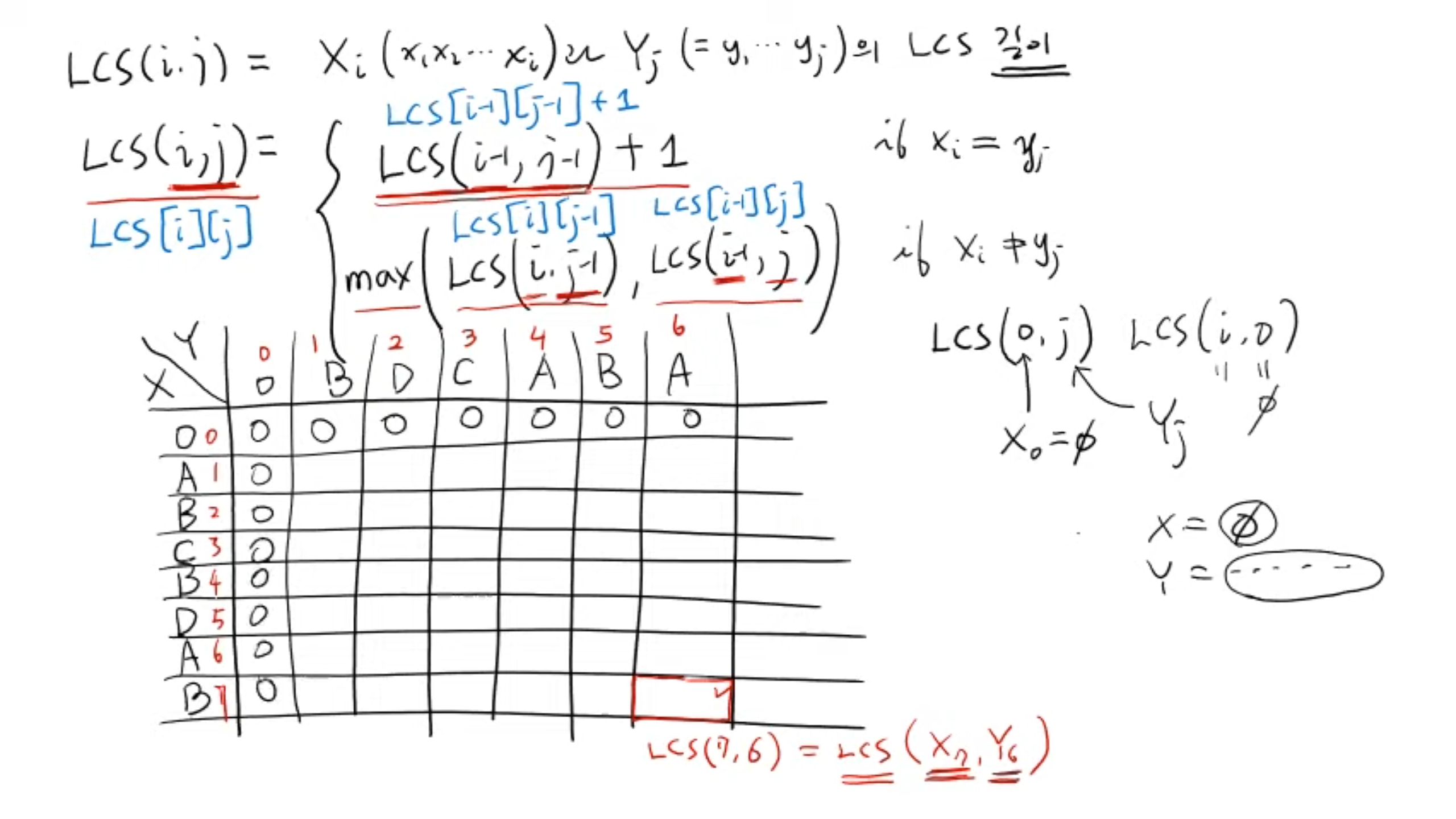

LCS(0, j) 일 때는 X 가 빈 문자열이므로 공통된 것을 찾을 수 없다.

LCS(i, 0) 일 때는 Y 가 빈 문자열이므로 공통된 것을 찾을 수 없다.

빨간 네모칸이 LCS[i][j]가 될 것이다.
그리고 위에서 점화식을 세웠듯이 LCS[i][j]를 구하기 위해서는
마지막 문자가 같은 경우와 다른 경우를 고려해야 한다.

같은 경우
**LCS[i-1][j-1] + 1 (빨간 네모칸의 왼쪽 대각선 위)**

다른 경우이면서 X의 마지막 문자열이 포함된 경우
**LCS[i][j-1]  (빨간 네모칸의 왼쪽)**

다른 경우이면서 Y의 마지막 문자열이 포함된 경우
**LCS[i-1][j] (빨간 네모칸의 위쪽)**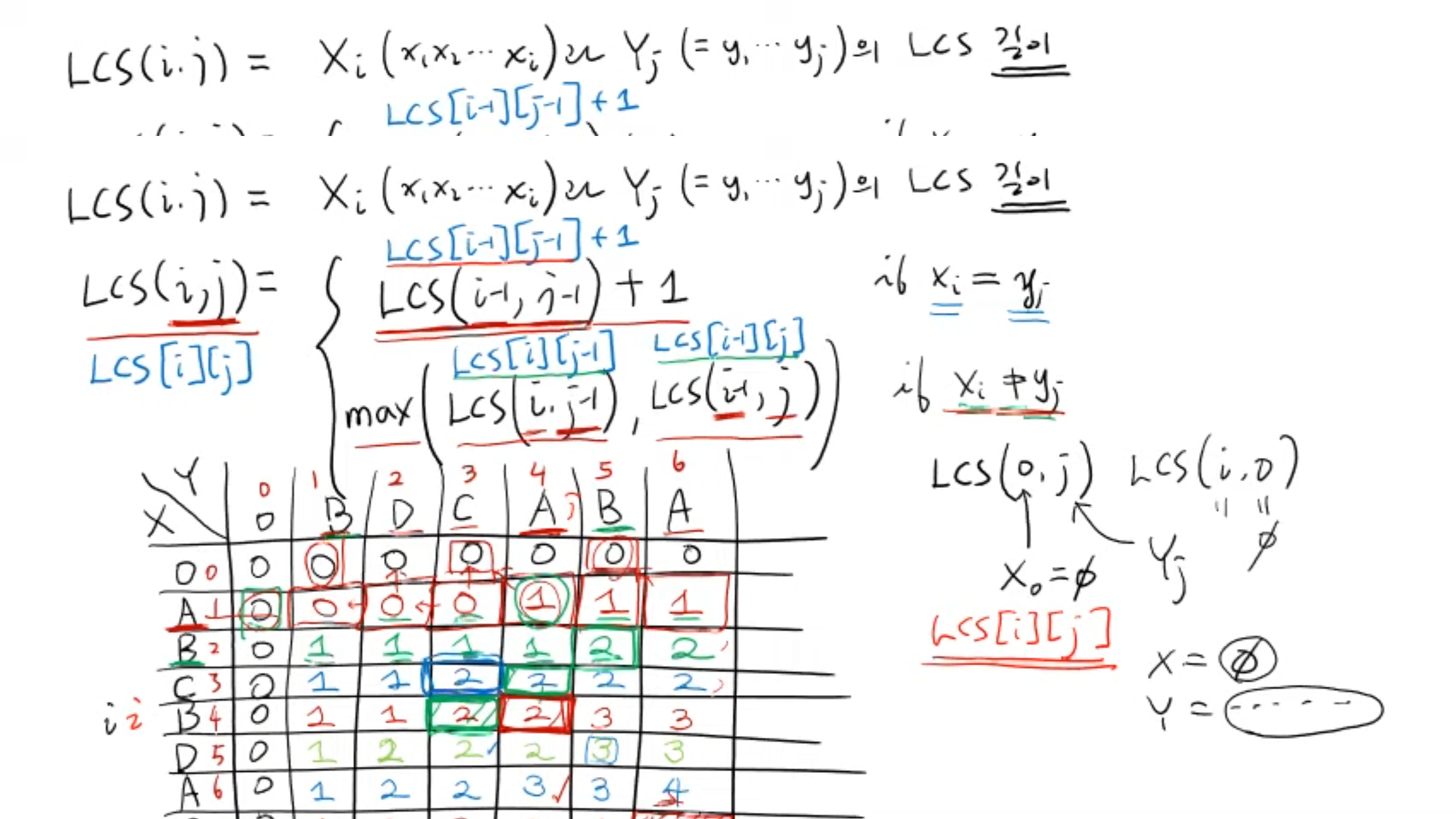

이제 비교하면서 같다면 대각선 왼쪽 위의 값에 1을 더하면 되고,
다르다면 왼쪽과 위쪽 값을 비교해서 더 큰 값을 가져오면 된다!

칸의 개수 = n * m
그리고 값을 구하는 시간은 상수시간 O(1)

시간복잡도 : O(nm)