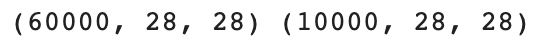신경망 학습(Training Neural Network)

요약

순전파 - > 손실 함수 -> 역전파(경사하강법으로 검증)

---

예시

UP & Down 게임
1. 맞추는 사람은 조건에 맞는 숫자를 1개 예측(순전파)
2. 출제자는 정답 숫자를 예측한 숫자보다 크면 Up, 작으면 Down(손실함수)
3. 알려준 정보를 바탕으로 조건에 맞는 새로운 숫자를 예측(역전파-순전파)

개념

1. 순전파(Foward Propagaiton)

입력층에서 입력된 신호가 은닉층 연산을 거쳐 출력층에서 값을 내보내는 과정.
신호가 전달되는 과정을 순전파라 한다.

• 연산과정
  1). 입력층으로부터 신호를 전달받습니다
  2) 입력된 데이터에 가중치-편향 연산을 수행
  3). 가중합을 통해 구해진 값은 활성화 함수를 통해 다음층으로 전달.

2. 손실 함수(Loss function)

출력된 값과 데이터 타겟값을 손실 함수에 넣어 손실(Loss or Error)을 계산.

대표적인 손실 함수는 MSE(Mean-Squared Error), CEE(Cross-Entropy Error) 이 있습니다.

* 각 문제별 사용 손실 함수

회귀 : MSE, MAE

이진분류 : binary_crossentropy

다중분류 : categorical_crossentropy , sparse_categorical_crossentropy

3. 역전파(Backward Propagation)

역전파(Backpropagation)는 순전파와 반대 방향으로 손실(Loss or Error) 정보를 전달해주는 과정입니다.

순전파 : 입력신호 정보를 입력층->출력층까지 전달

역전파 : 손실정보를 출력층->입력층까지 전달

각 가중치를 얼마나 업데이트 해야할 지 구하는 알고리즘입니다.

신경망은 매 반복마다 손실을 줄이는 방향으로 가중치를 업데이트 합니다.
이 손실을 줄이기 위해서 가중치 수정 방향을 결정하는 것이 경사하강법(Gradient Descent, GD) 입니다.

4. 경사하강법(Gradient Descent)

경사 하강법은 일반적으로 머신러닝에서 사용되는 손실 함수(비용 함수)를 최적화하는 데 사용됩니다. 손실 함수는 모델의 예측 값과 실제 값 사이의 오차를 계산합니다. 경사 하강법은 이 손실 함수를 최소화하는 가중치와 편향 값을 찾는 데 사용됩니다.

경사 하강법은 시작점에서 시작하여, 매 스텝에서 현재 위치에서의 기울기(gradient)를 계산하고, 그 기울기가 낮은 쪽으로 이동하는 과정을 반복하여, 함수의 최솟값에 도달합니다. 이 과정에서, 기울기의 반대 방향으로 이동하는데, 이를 "경사 하강"이라고 합니다.

매 Iteration마다 해당 가중치에서의 비용 함수의 도함수(=비용함수를 미분한 함수)를 계산 하여 경사가 작아질 수 있도록 가중치를 변경합니다.

5. 역전파 가중치 갱신

편미분과 Chain rule(연쇄법칙)이 사용됩니다.

6. 옵티마이저

경사를 내라가는 방법을 결정

모든 데이터를 다 사용하여 가중치를 갱신하기에 데이터가 많아질수록 계산과정이 매우 오래 걸립니다. 그걸 보완하기 위해 확률적 경사 하강법이 등장합니다.

7. 확률적 경사하강법과 미니배치 경사 하강법

1). 확률적 경사 하강법(Stochastic Gradient Descent, SGD)

전체 데이터 중 하나의 데이터를 뽑아서 신경망에 입력 후 손실을 계산합니다.
가중치를 빠르게 업데이트 가능하다는 장점이 있지만 1개의 데이터만 보기에 학습 과정 중 불안정함을 보입니다.

2). 미니 배치(Mini-batch) 경사 하강법
N개의 데이터로 미니 배치를 구성해 해당 미니 배치를 신경망에 입력 후 이 결과를 바탕으로 가중치를 업데이트 합니다.

• 배치 사이즈
  - 미니 배치 경사 하강법에서 사용하는 미니 배치의 크기를 배치 사이즈 라고 합니다.
  - 일반적으로 배치 사이즈는 2의 배수로 설정합니다.

8. of Data, Epoch, 배치 사이즈, iteration의 관계

데이터(data): 모델 학습에 사용되는 입력 데이터 세트입니다.

에포크(epoch): 전체 데이터 세트가 모델에 대해 한 번 훈련된 것으로 간주됩니다. 에포크의 수는 학습 프로세스에서 데이터 세트가 모델에 대해 몇 번 반복해서 사용되는지 결정합니다.

배치 사이즈(batch size): 학습 데이터를 여러 개의 작은 묶음(batch)으로 나누는 방법을 결정합니다. 각 묶음은 모델의 가중치 및 편향 업데이트에 사용됩니다.

이터레이션(iteration): 각 배치의 데이터가 모델에 대해 한 번 전달되는 것을 의미합니다. 이는 모델이 각 배치를 처리하고 결과를 출력하고 가중치를 업데이트하고 다음 배치를 처리하기 위해 준비되는 과정입니다.
(순전파-역전파 1회, 즉 가중치를 한 번 수정하는 단위)

데이터의 수(# of Data), 배치 사이즈, Iteration 이 아래와 같은 식을 만족한다는 것을 알 수 있습니다.

of Data = Batch_size X Iteration

예시문제

데이터셋에 있는 전체 데이터의 수가 1000개 이고 batch_size=8, epochs=5 로 설정하였다면 학습이 종료될 때까지 Iteration 은 몇 회 일어날까요?

데이터셋에 있는 전체 데이터의 수가 1000개이며, 배치 크기(batch_size)가 8이므로 하나의 배치에는 8개의 데이터가 포함됩니다.

따라서 전체 데이터셋을 처리하기 위해 필요한 배치 수는 1000 / 8 = 125입니다.

에포크(epochs)가 5이므로 전체 학습 과정은 5번의 에포크 동안 진행됩니다.

따라서 학습이 종료될 때까지 전체 이터레이션(iterations) 수는 다음과 같이 계산할 수 있습니다:

총 이터레이션 수 = 배치 수 x 에포크 수 = 125 x 5 = 625

따라서, 이 모델 학습에서는 625번의 이터레이션이 발생합니다.

---

---

Tensorflow 신경망 예제

Fashion MNIST 예제

이 예제는 이진분류, 다중분류, 회귀 중 어디에 속할까?
정답 : 다중분류

1. 필요한 패키지,라이브러리 불러오기

import numpy as np
import pandas as pd
import tensorflow as tf

2. 데이터셋을 불러오고 학습 데이터셋과 시험데이터셋으로 나누고 픽셀값을 정규화

from tensroflow.keras.datasets import fashion_mnist
(X_train,y_train), (X_test, y_test) = fashion_mnist.load_data()

print(X_train.shape, X_test.shape)

• 이미지 데이터에서는 정규화 과정이 중요.
  X_train, X_test = X_train / 255.0, X_test / 255.0

데이터 확인

import matplotlib.pyplot as plt
for i in range(9):
    plt.subplot(3, 3, i+1)    
    plt.imshow(X_train[i], cmap=plt.get_cmap('gray')) # 데이터에 맞게 이미지를 흑백으로 출력합니다.
    plt.axis('off')    
plt.show()

3. 레이블 구성 확인

np.unique(y_train)

array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9], dtype=uint8)

4. 신경망 구축

from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense, Flatten
model = Sequential()
model.add(Flatten(input_shape=(28, 28)))
model.add(Dense(10, activation='softmax')) # 출력층

model.compile(optimizer='adam', # 옵티마이저
loss='sparse_categorical_crossentropy', # 손실함수
metrics=['accuracy']) # 학습 지표

model.summary()

Model: "sequential"
_________________________________________________________________
 Layer (type)                Output Shape              Param #   
=================================================================
 flatten (Flatten)           (None, 784)               0         
                                                                 
 dense (Dense)               (None, 10)                7850      
                                                                 
=================================================================
Total params: 7,850
Trainable params: 7,850
Non-trainable params: 0
_________________________________________________________________

질문

❗️ 코드에서 출력층의 노드 수는 몇 개인지, 출력층의 활성화 함수는 무엇인지, 손실 함수는 어떻게 지정하였는지에 주목해봅시다.

정답 : 입력값은 이전의 히든 레이어(Flatten)에서 784개의 뉴런으로 전달되었습니다. 따라서 출력층에서는 각 입력값마다 10개의 출력값을 만들어 내야 하므로, 총 가중치 개수는 784 x 10 = 7840개가 됩니다.
또한, 각 출력 뉴런마다 하나의 편향이 필요합니다. 출력층의 뉴런 개수가 10개이므로, 편향의 개수도 10개입니다.
따라서, 총 파라미터 개수는 7840개의 가중치와 10개의 편향을 더한 7850개가 됩니다.

5. 신경망 모델 사용 및 평가

model.fit(X_train, y_train, epochs=10)
model.evaluate(X_test, y_test, verbose=2)

313/313 - 1s - loss: 0.4639 - accuracy: 0.8340 - 983ms/epoch - 3ms/step
[0.4639376103878021, 0.8339999914169312]