Container::rbtree

YP J·2022년 10월 10일
0

ft_container

목록 보기
8/8
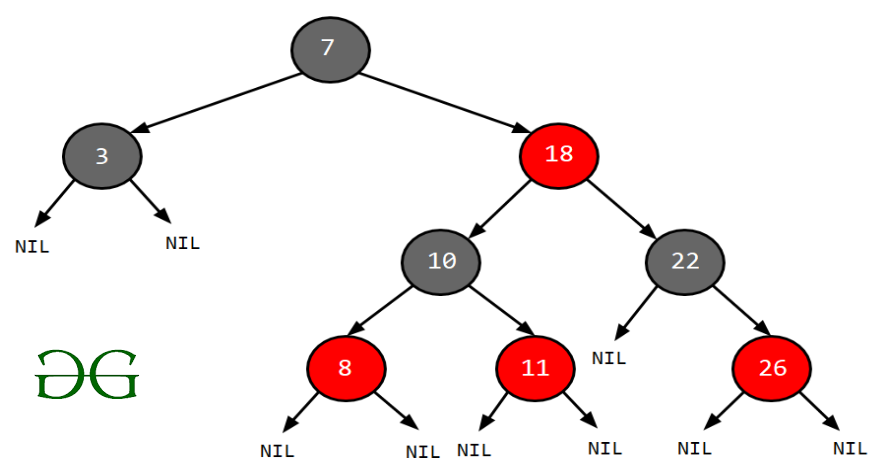
post-thumbnail

A red-black tree is a balanced binary search tree
https://velog.io/@zhy2on/Red-Black-Tree

rbtree rules

Rules That Every Red-Black Tree Follows:

  • Every node has a color either red or black.

  • External Property : 모든 external node들은 검정(Black)이다.

  • Root Property : The root of the tree is always black.

  • Internal Property :빨강(Red)노드의 자식은 검정(Black)이다. == No Double Red(빨간색 노드가 연속으로 나올 수 없다.) 

    • There are no two adjacent red nodes (A red node cannot have a red parent or red child).
    • red node가 붙어 있을수 없다.

  • Depth Property: Every path from a node (including root) to any of its descendants NULL nodes has the same number of black nodes.

    • 루트에서 부터 모든 라인의 leaf node까직 블랙 노드 수가 같다.

  • All leaf nodes are black nodes.

Comparison with AVL Tree:

  • 삽입 삭제보다 검색이 빈번한 작업이라면 -> AVL tree
    • 검색은 균형이 더 잘 잡힌 AVL tree가 더 빠를수 있기 때문
    • AVL 트리 가 rb트리 보다 균형이 더 잘 잡하여있지만
    • avl트리는 삽입 삭제에서 더 많은 rotation이 발생할수 있다. ( avl 은 높이차이가 1보다 커지면 rotation시켜서 균형 유지)
  • 삽입 삭제가 빈번한 경우 rbtree
    • 삽입삭제 할땐 규칙이 덜 복잡한 rb 트리가 유리

How does a Red-Black Tree ensure balance?

https://zeddios.tistory.com/237

rbtree simulation (삽입)

  • 처음 노드 빨강으로 삽입 했다가 (모든 노드는 빨강으로 삽입)

  • Root property에 의해 블랙으로~

  • 2,8 삽입 해보면

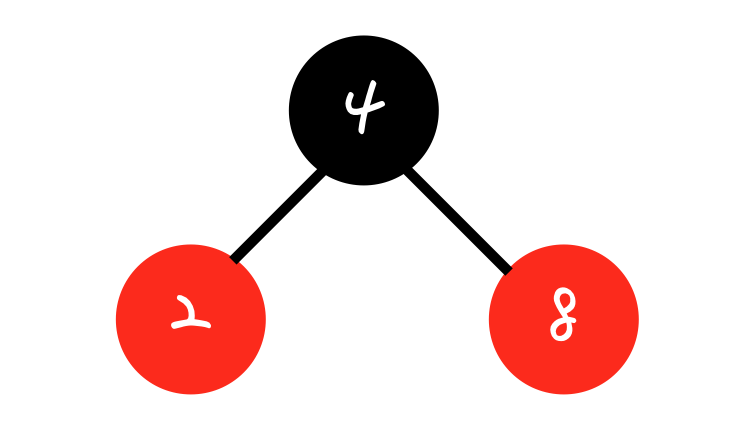
  • 3 을 삽입해보면

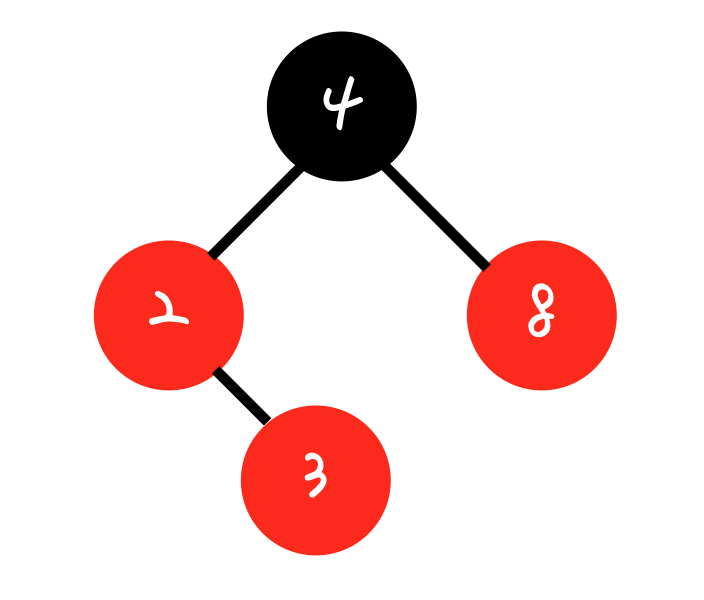
  • 이렇게 되면 Internal property 위반.

    • red 의 자식은 블랙이여야 한다.

  • 이러한 문제가 Double Red -> 이걸 해결해야만 균형 유지된다.

Double RED 해결 전략

  1. Restructuring
  2. Recoloring

  • 현재 insert된 노드의 uncle node 의 색깔에 따라 수행하는 절차가 다르다. (엉클 : 부모(v)의 형제(w) 노드)

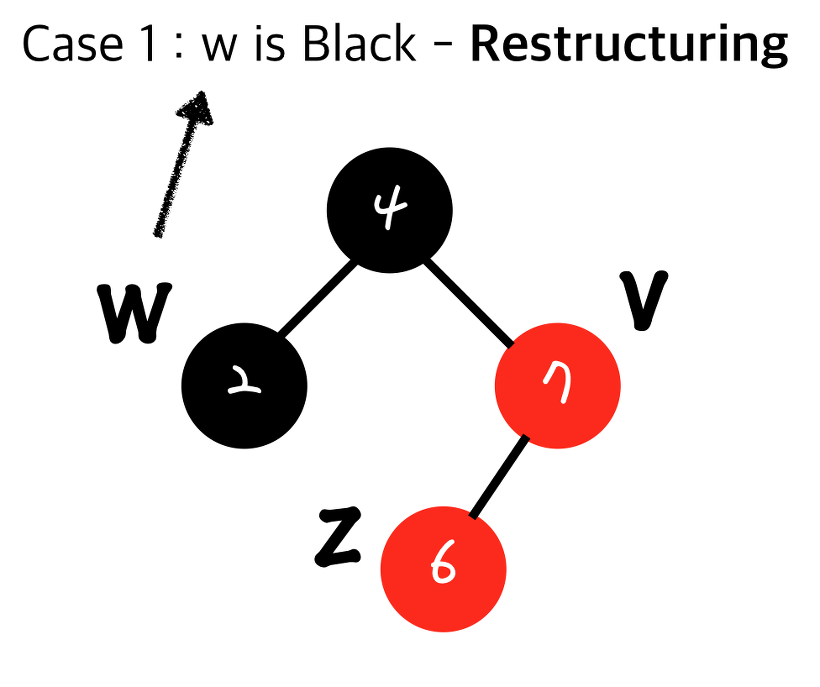
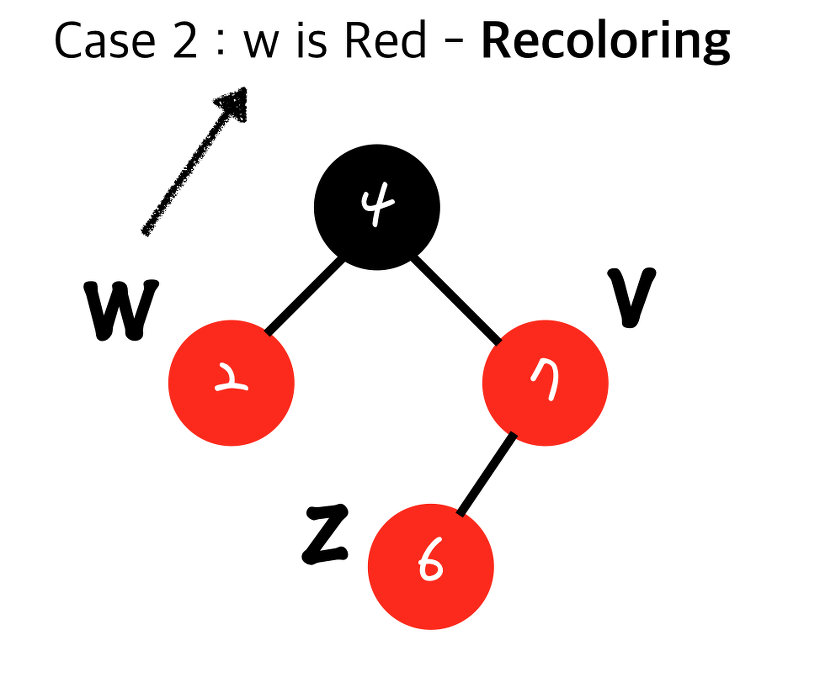
  • W 가 검정일땐 Restructuring

  • W 가 빨강일땐 Recoloring 수행

Restructuring

  • 현재 insert 된 노드(z)와 내 부모, 그리고 부모의 부모(Grand Parent)를 가지고( 총3개 노드) 진행된다

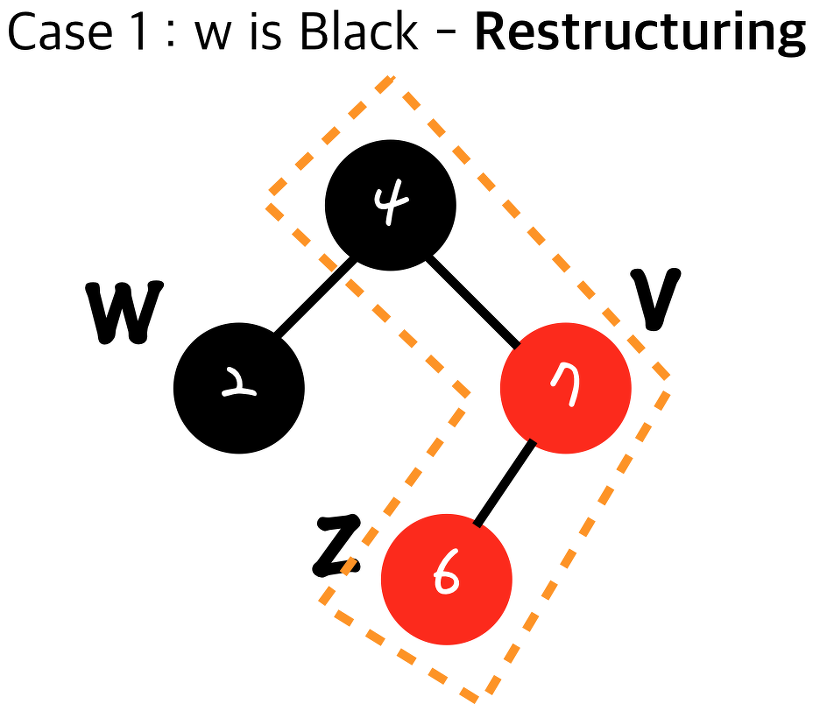
    1. 나(z)와 내 부모v , 부모의 부모(G)를 오름차순으로 정렬.
  • 중간 값이 parent자리에 가고, 나머지 값이 중간 값의 왼쪽 오른쪽 child가 되게 rotate한다.

  • 무조건 가운데 있는 값을 부모로 만들고 나머지 둘을 자식으로 만든다.

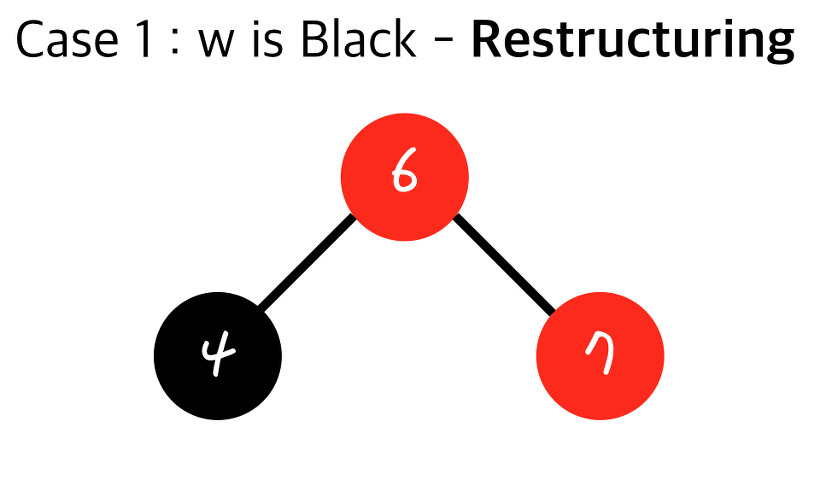
  • 부모가 된 노드를 검정으로 만들고 나머지 두 자식은 레드로 만든다.

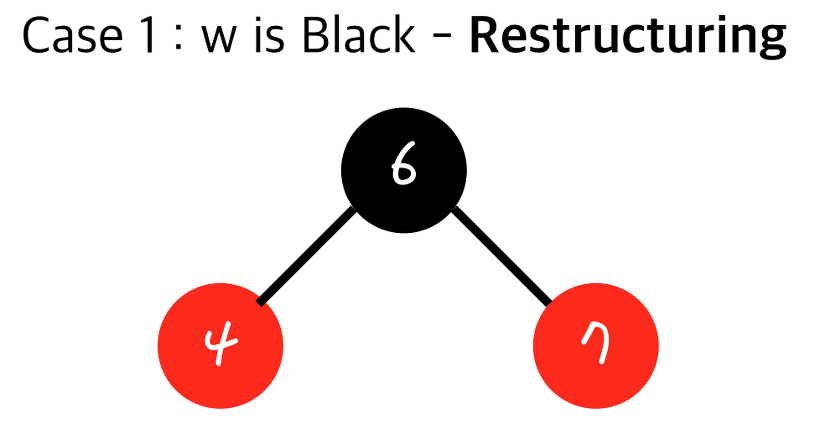
  • 원래 4의 자식이었던 2를 추가해 주면 된다.

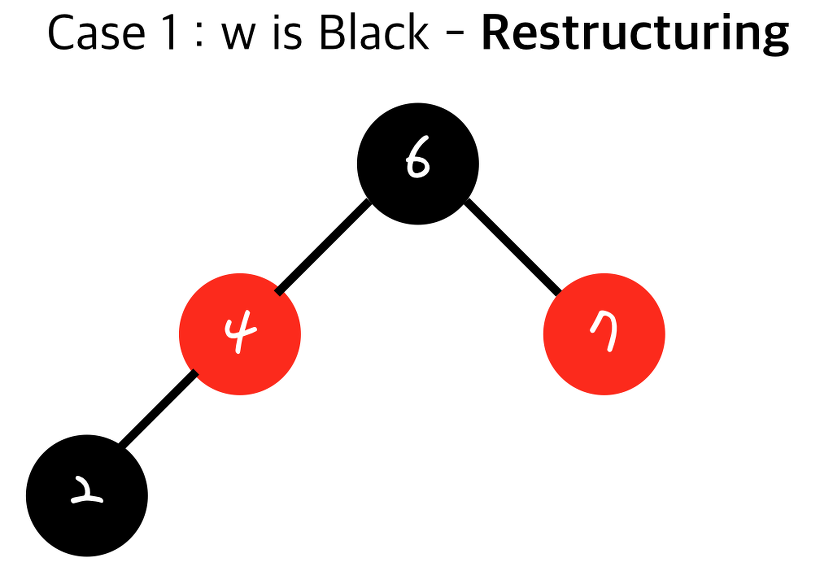
Restructuring은 다른 서브트리에 영향을 끼치지 않는다.
왜냐면 이 과정이 일어나도 블랙 노드의 개수에는 변화가 없으므로 다른 서브트리에 영향이 없다.

또한, Restructuring자체의 시간복잡도는 O(1)에 끝나지만, (순서결정시간 - 상수시간, 트리로 만드는시간 - 상수시간, 원래있던 노드들의 구조들을 바꿔주는 시간 - 상수시간)

 Restructuring은 어떤 노드를 insertion한 뒤 일어나므로 총 수행시간은 O(logn)이에요. 지금 현재 노드가 들어갈 위치를 먼저 찾아야 하기 때문이죠.

Recoloring


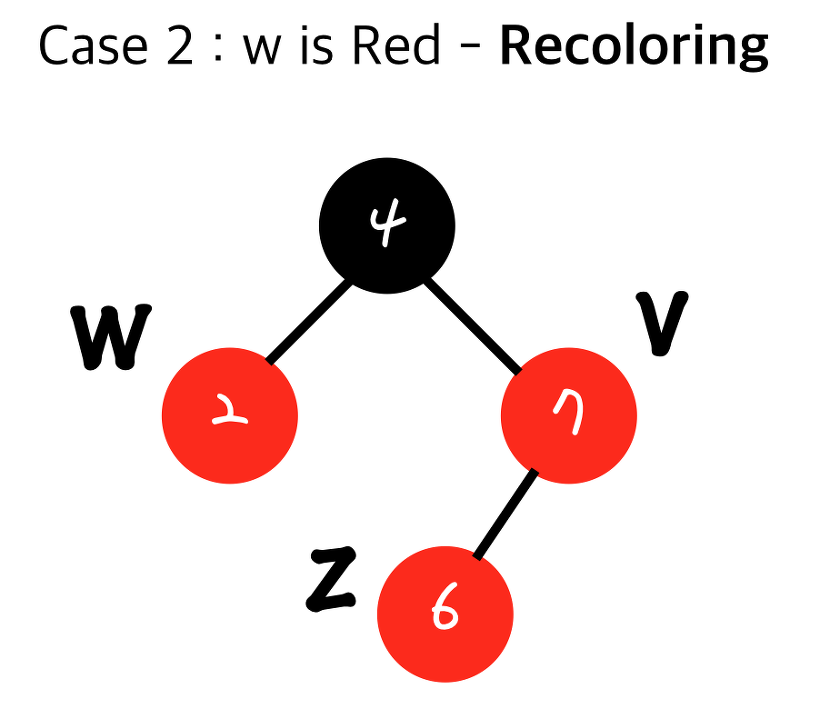
1. 현재 insert된 노드z 의 부모와 그 형제 w를 검정 으로 하고

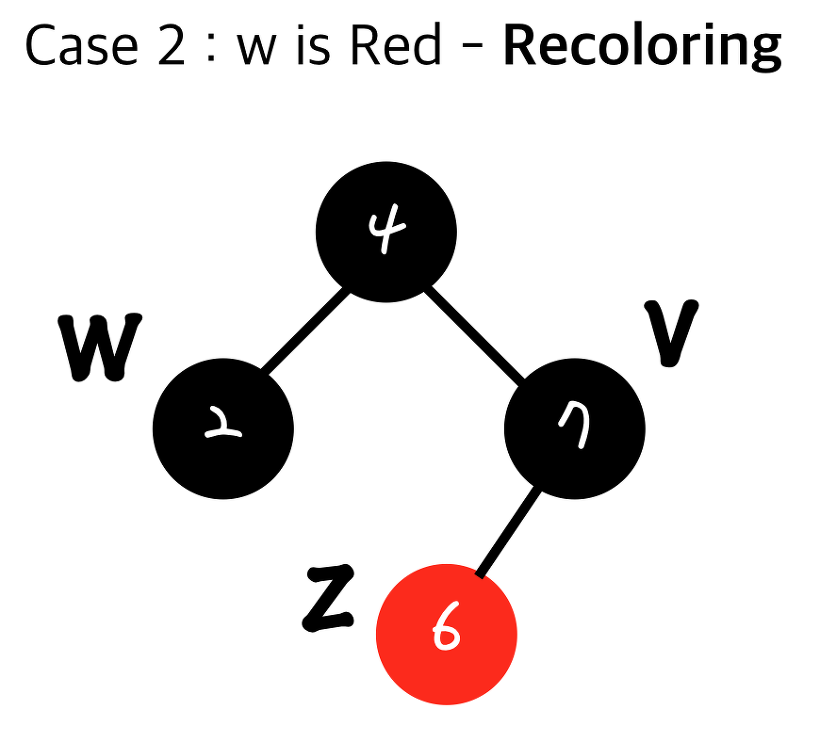
  • 부모의 부모를 G 빨강으로한다.

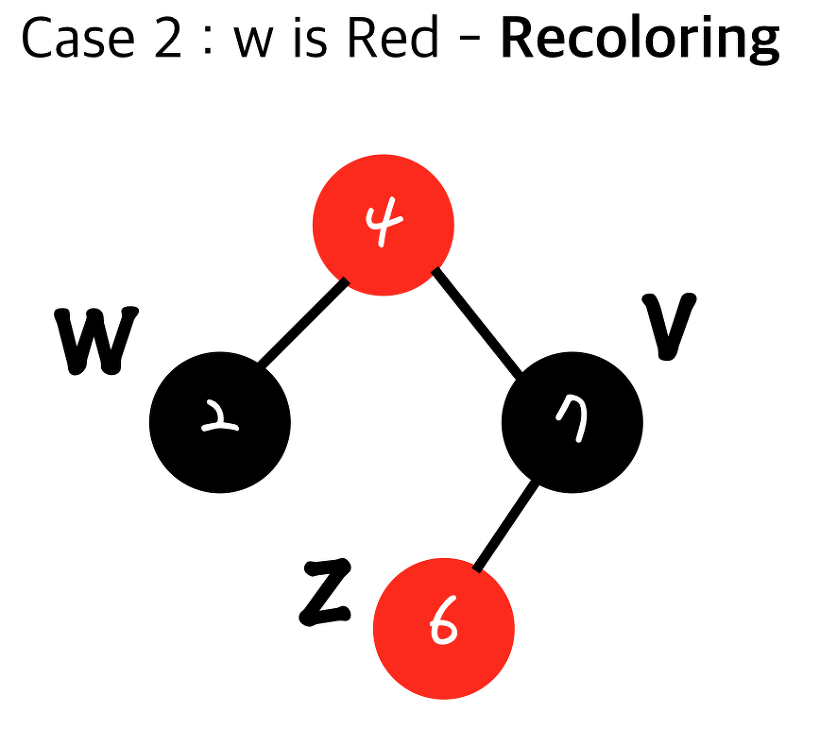
  • 만약 내 부모의 부모가 루트 노드이면 Root Property에 의해 검정으로 바꾼다.

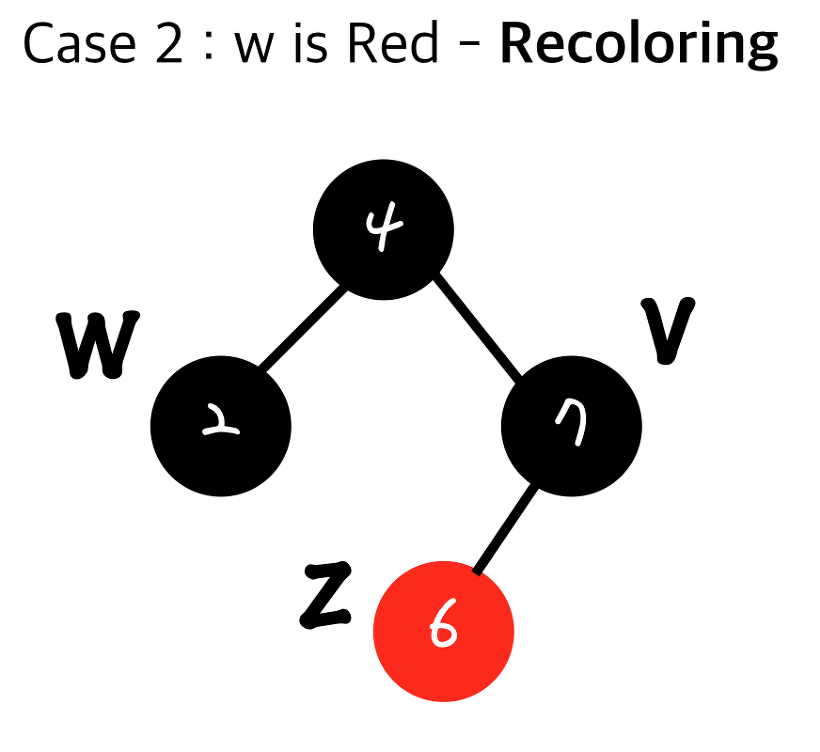
  1. 부모의 부모가 루트 노드가 아닐시 다시 Double red 발생할수 있다.

    -그럼 이 상태로 둬야할텐데,

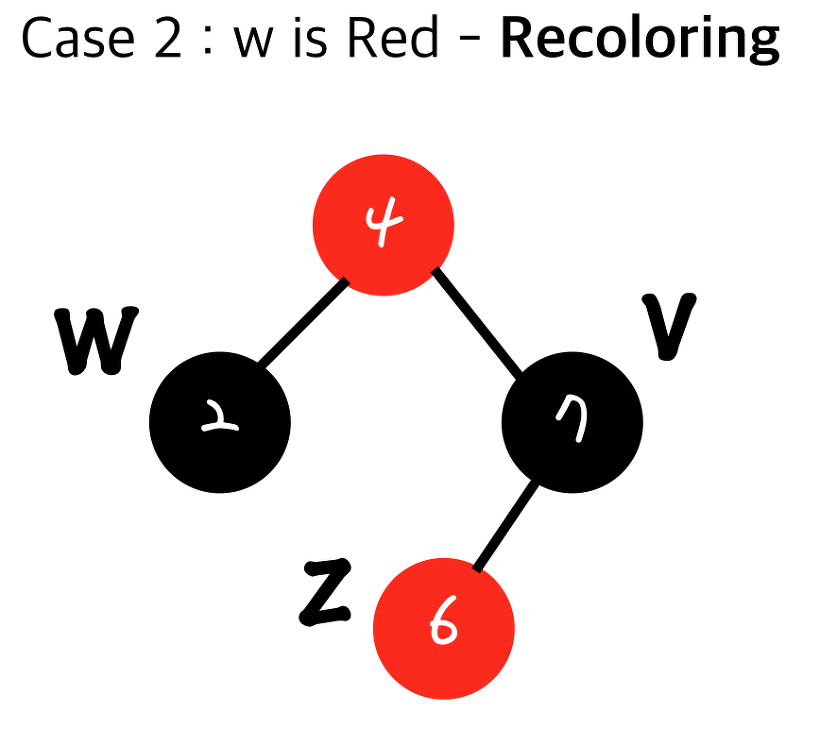
  • 이 4위에 또!!!!!!!!!!!사실은 또!!!! 빨강(Red)노드가 있을 수 있습니다.그럼 또 Double Red가 생겼죠? 즉, Recoloring의 경우 Restructuring과 다르게 propagation될 수 있습니다. 최악의경우 Root까지 갈 수 있게되죠.(logN)
  • 만약 4의 부모가 Red였다면!!!그냥 다시 4의 부모의 형제노드(uncle node)의 색깔을 보고!!!!!!Restructuring할건지, Recoloring할건지 결정해주면 됩니다.
  • 이 때 uncle node의 색깔이 검정(Black)이었다면 Restructuring을 하게되겠죠? 위에서 말했다시피, Restructuring은 다른서브트리에 영향을 끼치지 않습니다.그러니 Double Red는 이제 발생하지 않게되고 여기서 fix가 종료되게 되죠.
  • 하지만, uncle node의 색깔이 빨강(Red)였다면, Recoloring을 다시 하겠죠?Recoloring을 다 하고 나서, 또!11!!! Double Red가 생길 가능성이 있는 것이죠.

Q : 저렇게 막 내 부모랑 uncle노드를 막 검정으로 바꿔도돼??!! 레드블랙트리의 4번조건. Depth Property만족해?
A : 네. 만족합니다. Black Depth는 일제히 1증가하기 때문에 문제가 없습니다 :)

  • 서브트리에서 recoloring이 발생해도 전부 +1 이 되는거기 때문에 영향이 없다.

+어느 리프노드에서 루트노드까지 가더라도 Black Depth는 항상 같아야합니다. 

  • A: 그럼 가장 "짧은" Black Depth를 가지는 external node가 있고,

    • 블랙 노드만 있는 것

  • B : 가장 "긴" Black Depth를 가지는 external node가 있습니다. 

    • 블랙-레드-블랙-레드-블랙....
      (여기서 짧고 길다는 것은 정말 물리적으로 짧고 긴 것을 말해요.)(하지만 이 둘의 Black Depth는 반드시 같아야하죠.)

  • A,B의 최대 차이는 2배이다. 따라서 logN 과 2logN 의 차이.

### rbtree simulation (삭제)

출처: https://www.youtube.com/watch?v=6drLl777k-E

  1. 삭제전 rb 트리 속성 만족한 상태
  2. 삭제 방식은 일반적인 BST와 동일
    2. 삭제후 rb 트리 속성 위반 여부 확인
  3. rb위반 했으면 재조정
  4. 다시 rbtree 속성 만족

2: rb 트리에서 노드를 삭제할때 어떤 색이 삭제되는지가 속성 위반 여부 확인할때 매우 중요하다.

삭제되는 노드의 색?

  • 삭제하려는 노드의 *자녀가 없거나 하나라면
    • 삭제되는색 = 삭제되는 노드의 색
  • *여기선 유호한 값을 가지는 자녀를 의미( 닐노드 는 놉)
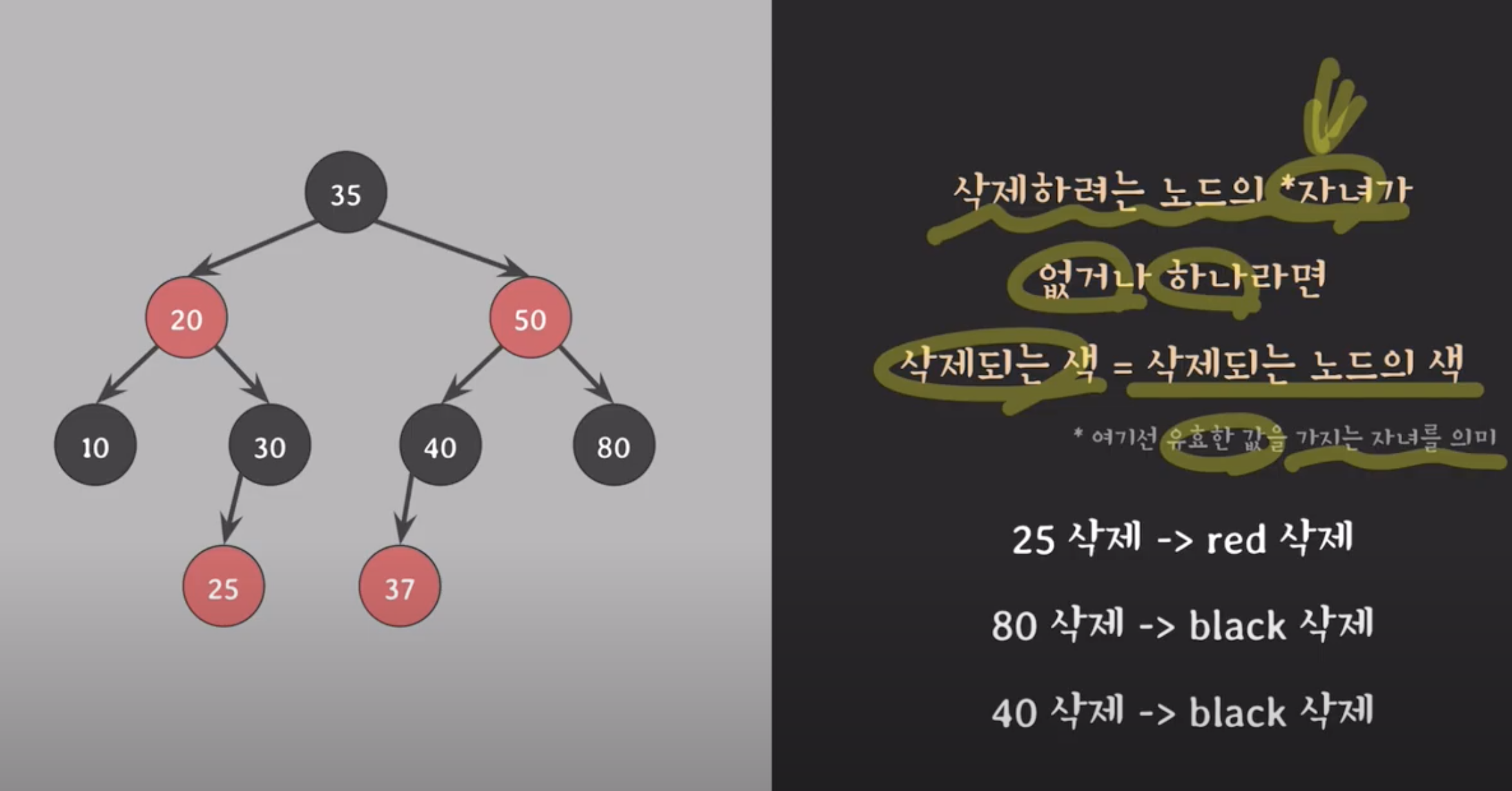
  • 삭제하려는 노드의 *자녀가 둘이라면 (*여기선 유호한 값을 가지는 자녀를 의미( 닐노드 는 놉))
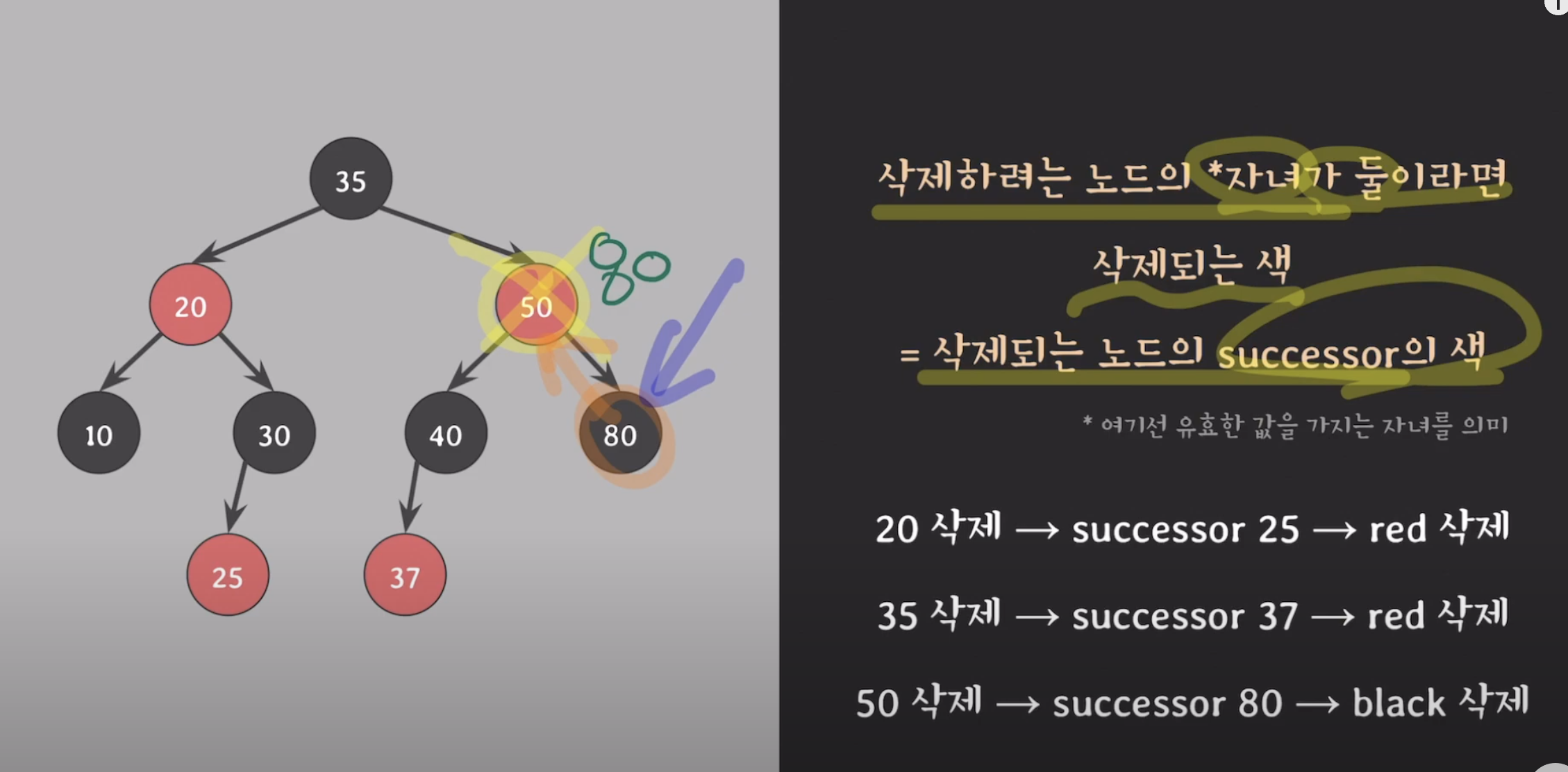
    • 삭제되는 색 = 삭제되는 노드의 successor(오른쪽 서브트리에서 가장 작은값)의색

예를 들어 50을 삭제할때 자식이 2명이므로 오른쪽의 서브트리에서 가장 작은값인 80 이 50의 색을 계승한다.

  • 즉 실제로는 50을 삭제 할때 50의 오른쪽 서브트리중 가장 작은 값인 80이 원래 있던 자리에서 삭제되고 (즉 블랙 삭제) 50의 자리와 색을 80이 계승한다.

요약

레드가 삭제 될때 속성위반 여부 확인

  • 삭제되는 색이 red 라면
  • 어떠한 속성도 위반하지 않는다.

**블랙이 삭제 될땐

  • 루트 노드는 블랙 (Root property
  • 노드가 레드 라면 자녀들은 블랙 ( Internal property
  • Depth property ( 얘는 항상 위반 된다.)

위 3가지 속성을 위반 할 수 있다.

위반 했을때 해결법

  • 루트 노드는 블랙 (Root property
    • 그냥 루트를 블랙으로 바꿔주면 됨.
  • **Depth property ( 얘는 항상 위반 된다.)

블랙이 삭제 되고 Depth property 위반 되었을때 해결법

  • extra black 부여 : 삭제된 색의 위치를 대체한 노드에 extra black을 부여 해놓고

  • extra black 노드가 red-black 인경우와 black-black 인 경우로 나뉘어서 해결한다.

  • extra black은 경로에서 하나의 블랙 노드로 카운트 한다.

  • black-black
    (그림에서 B,C는 색을 모르고 두가지노드가 색이 다를수도 있다.)

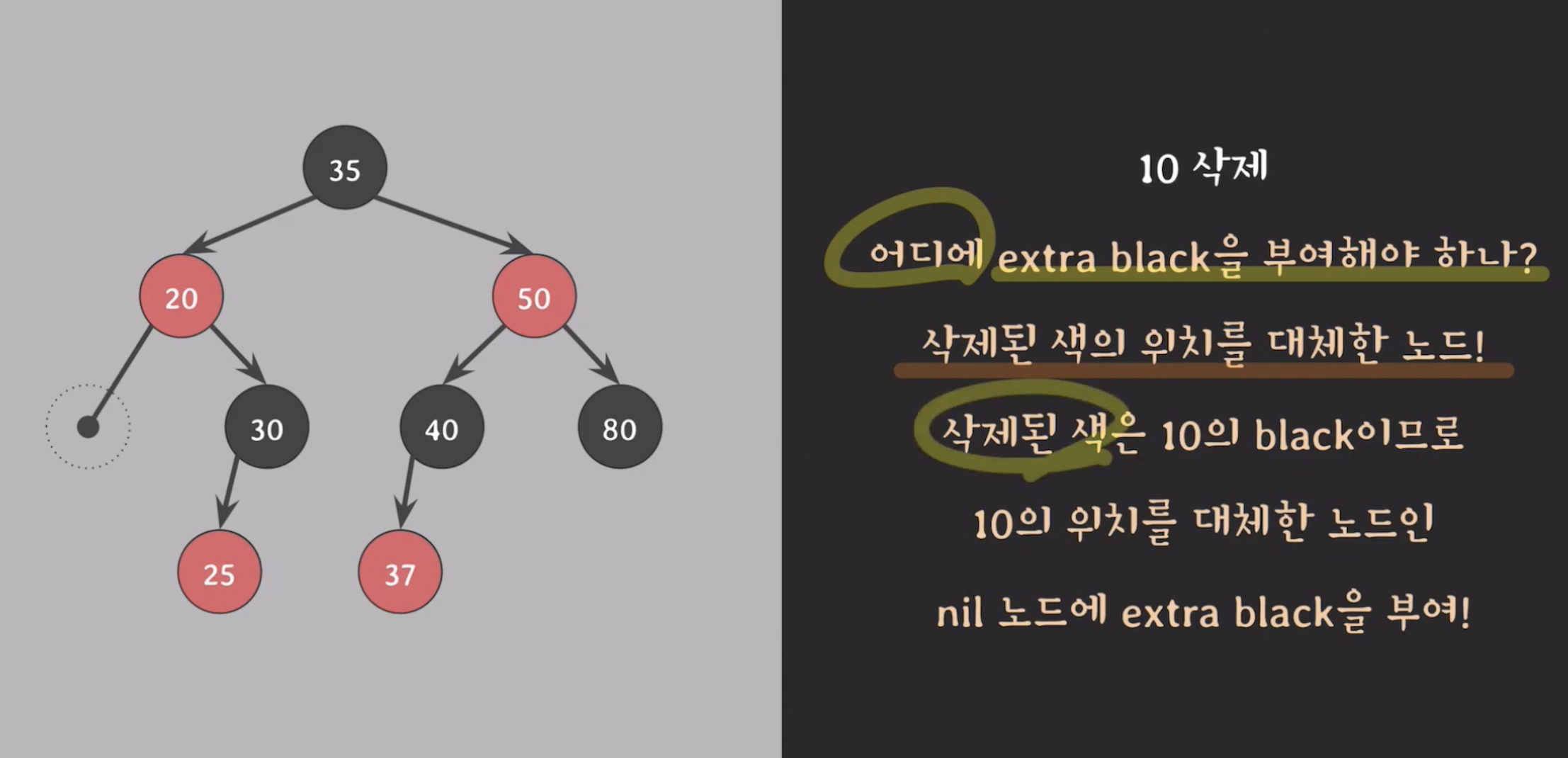
    • 20의 nill노드에 extra black을 추가해준다.

  • red-black

  • 30 삭제

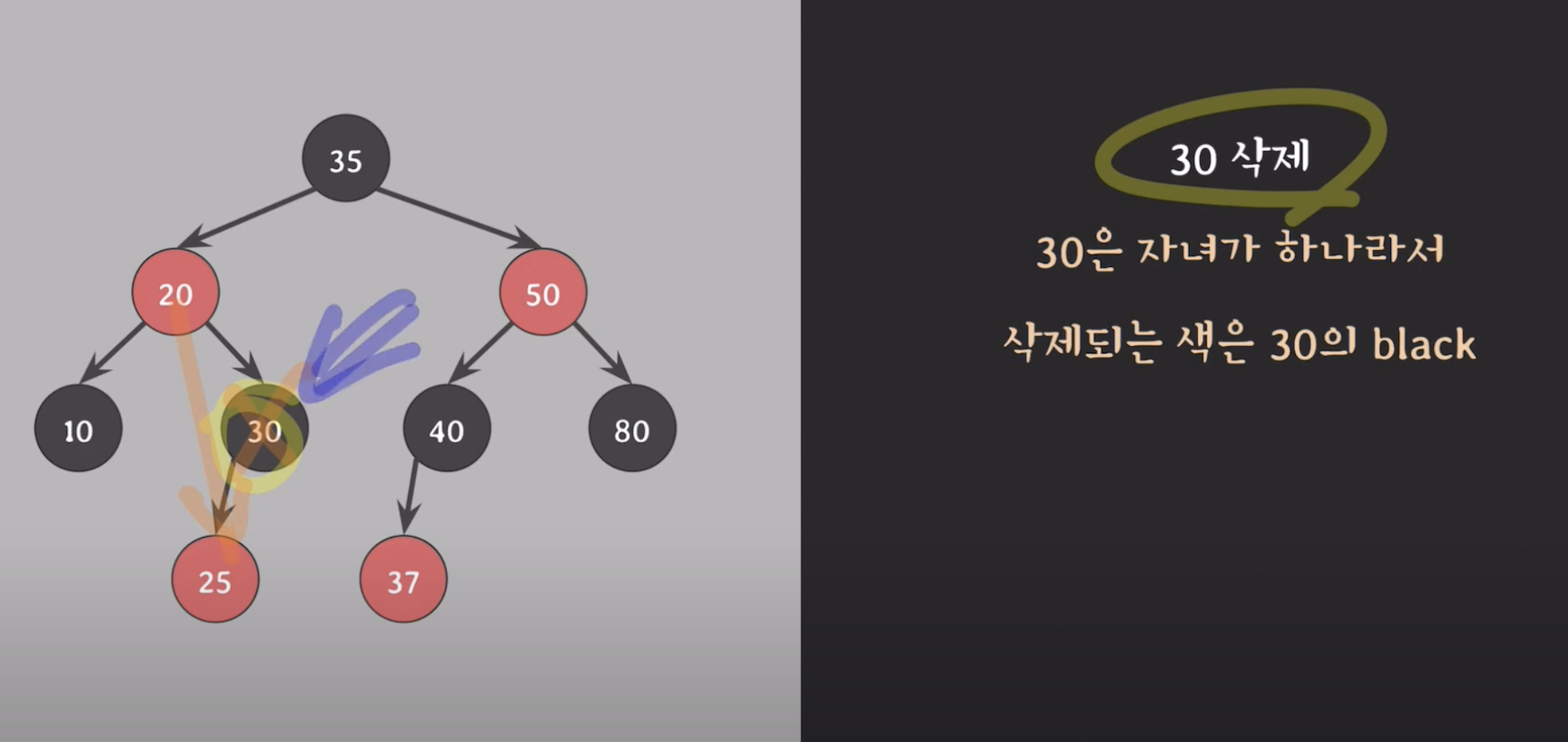
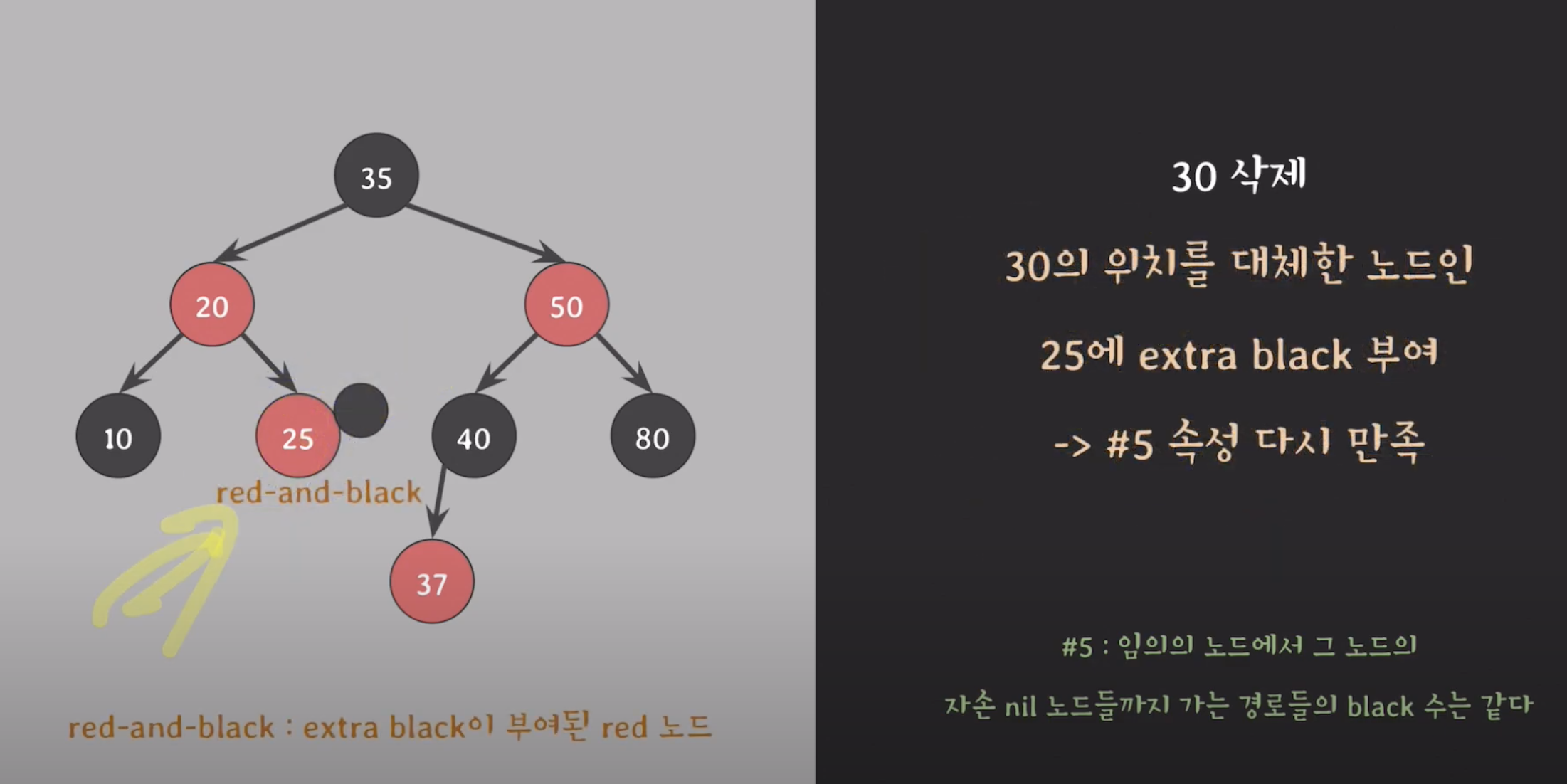
  • 삭제한 위치를 대체한 노드인 25 에 extra balck 부여

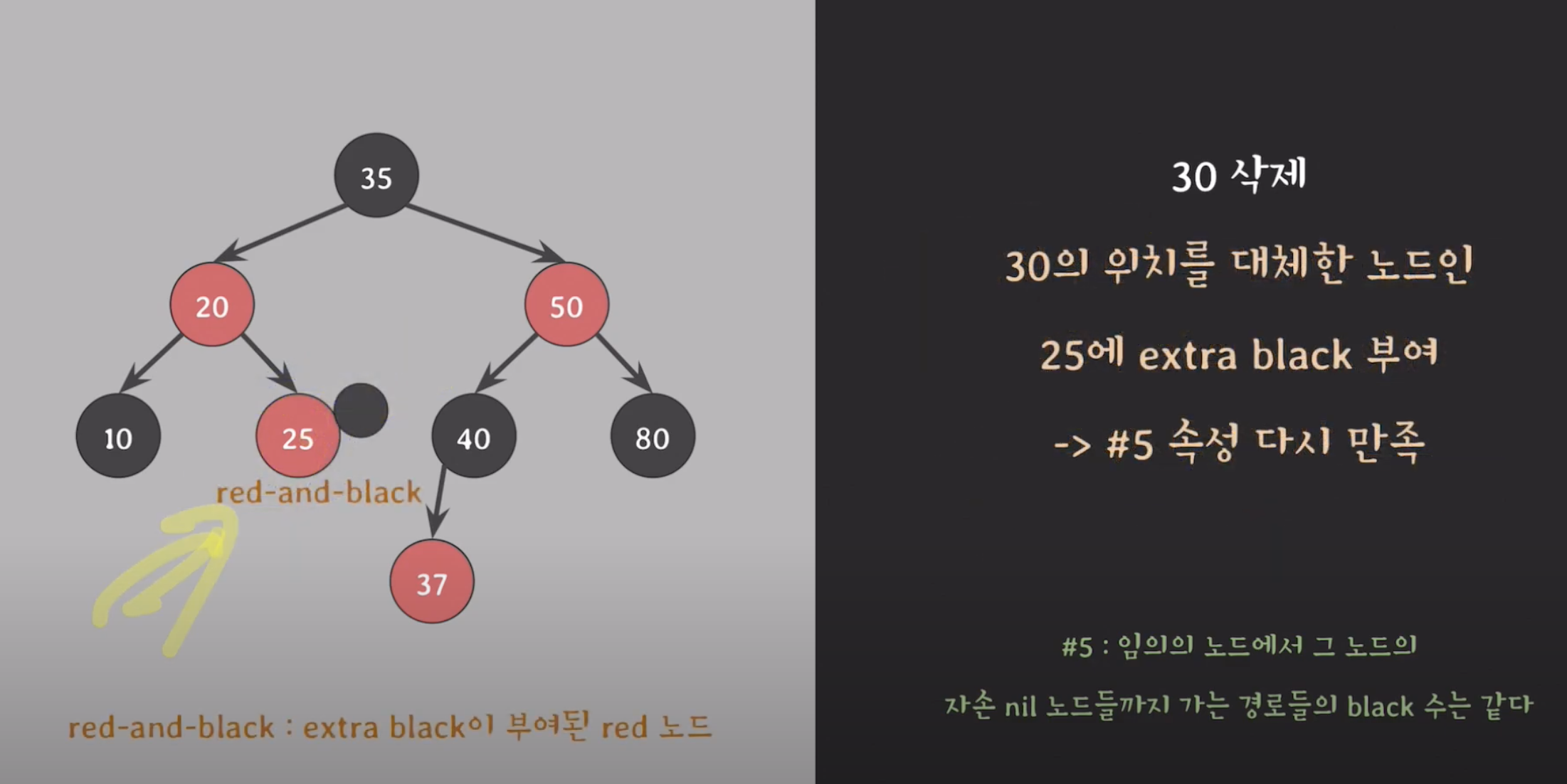
  • 50 삭제 예

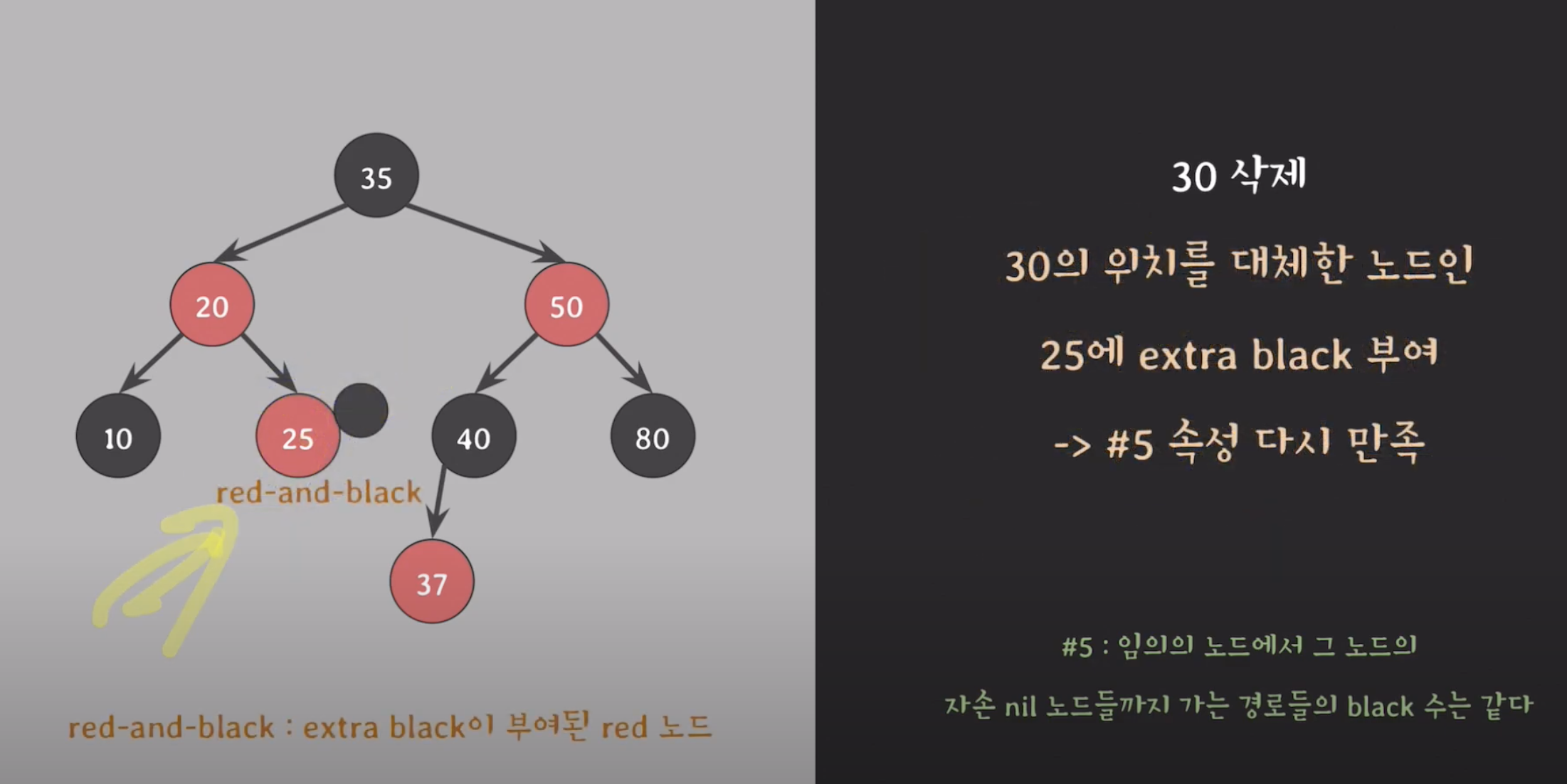
이제 extra black 을 해결은??

  • red-black -> black 으로 바꿔주면 해결 !

  • black - black 은 총 4가지 경우로 나뉘어서 해결 !

black - black 은 총 4가지 경우로 나뉘어서 해결

  • 그 4가지 기준은 doubly-black 의 형제의 색과 그 형제의 자녀들의 색으로 구분.

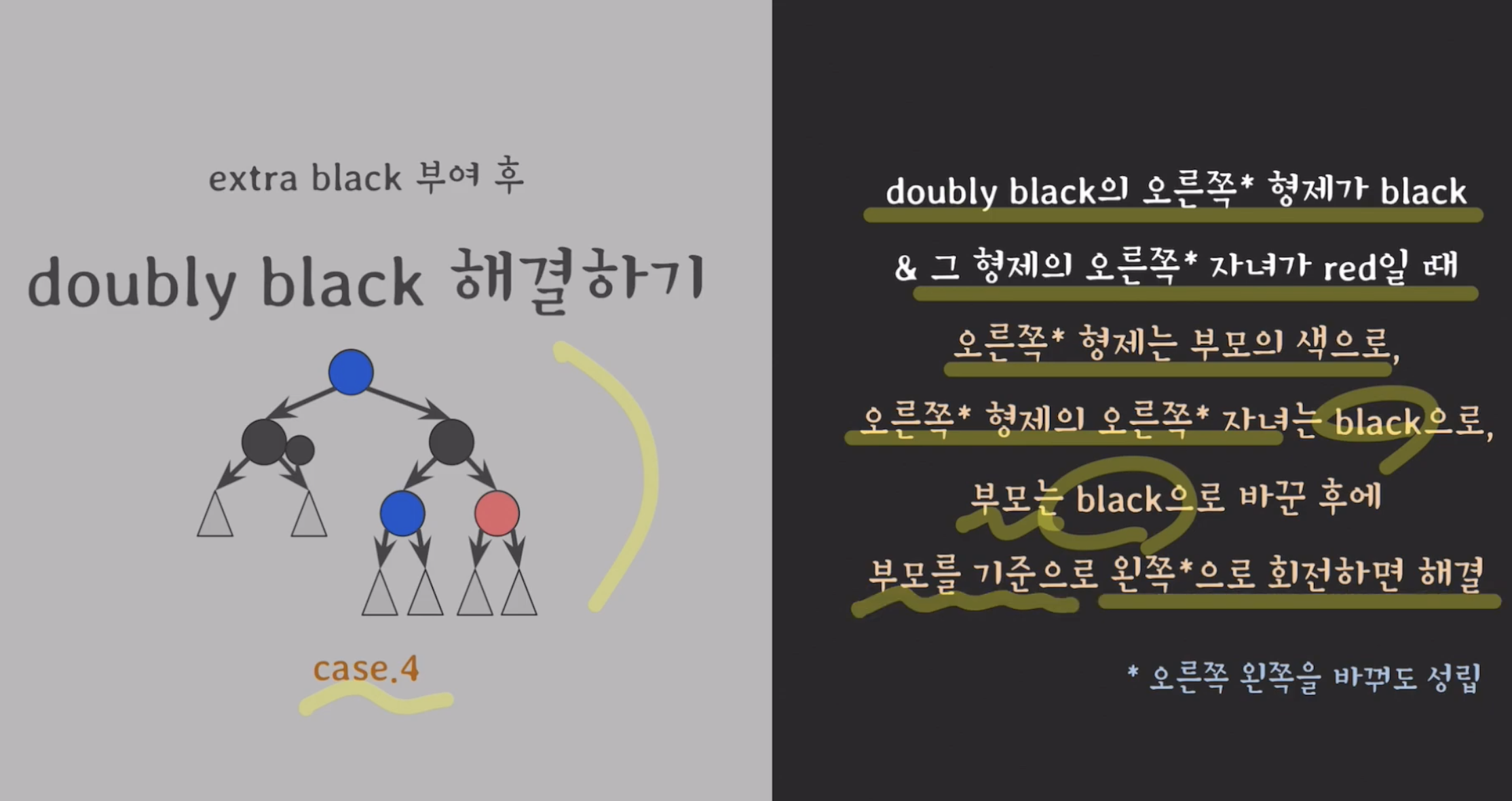
case 4.

  • A의 doubly black 을 해결하기위해

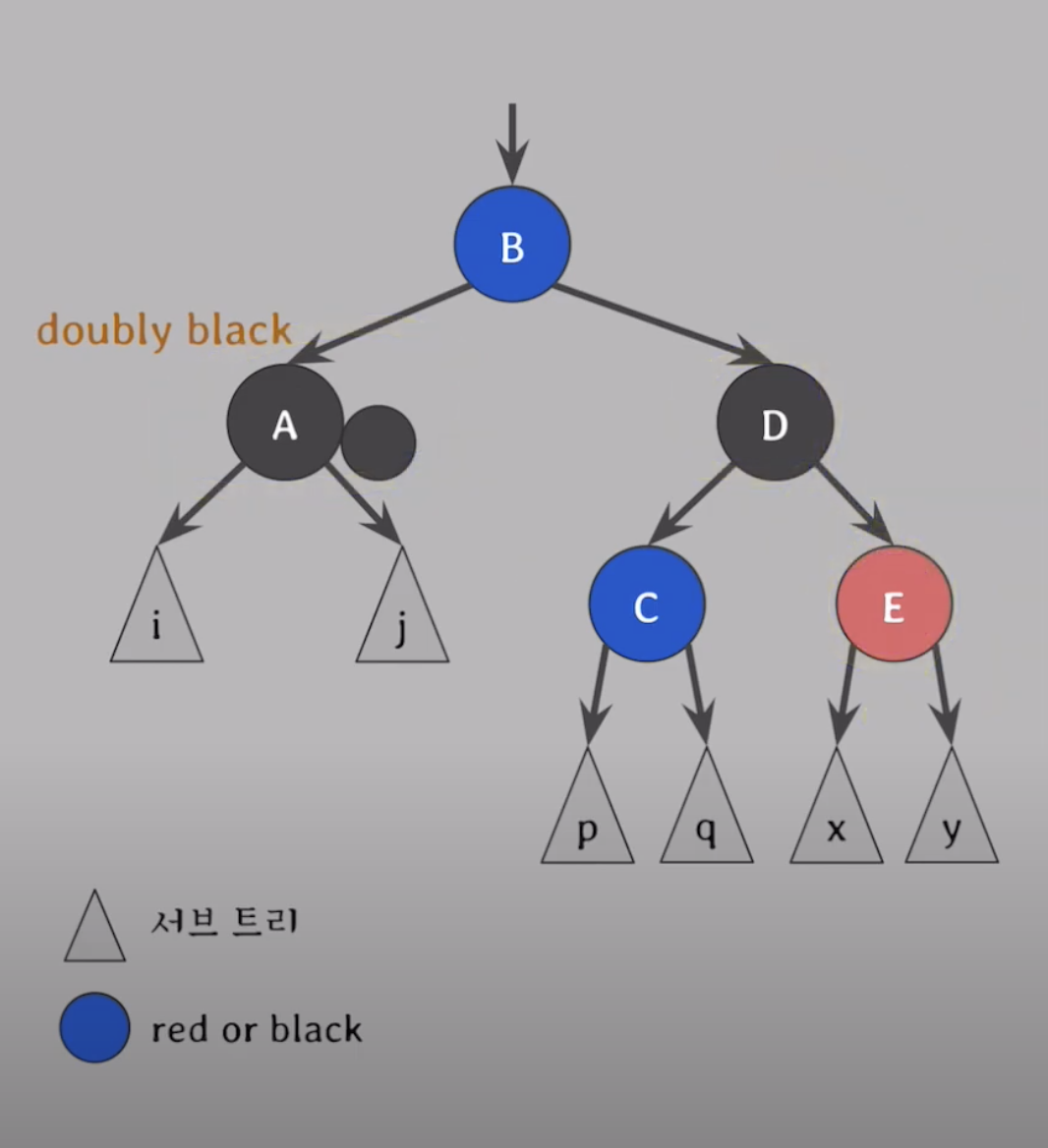
  • doubly 블랙의 오른쪽 형제가 블랙 & 그 형제의 오른쪽 자녀가 레드 일때.

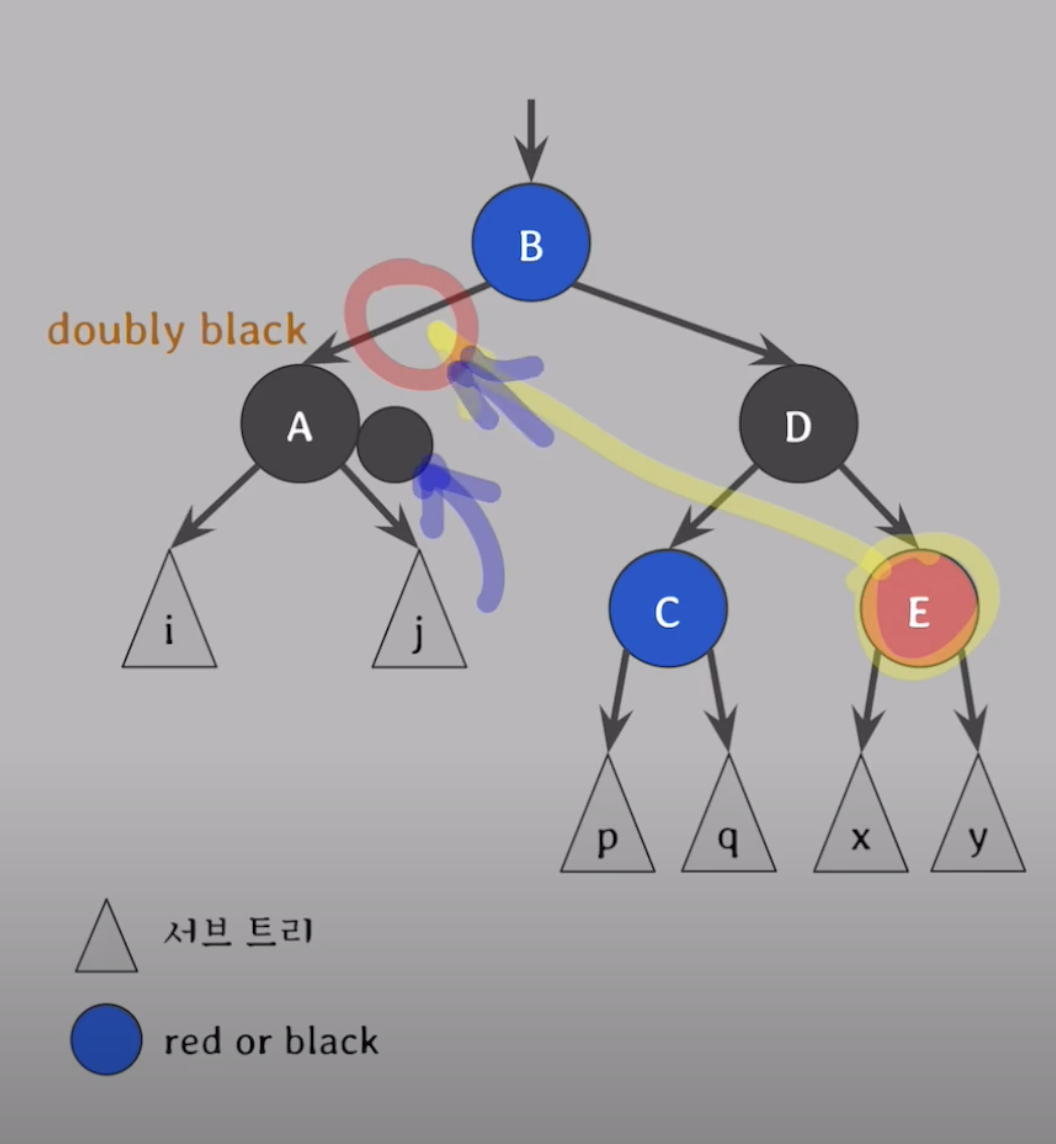
  • 그 red를 doubly black (A)위로 옮기고 옮긴 red로 extra black 전달해서 red-and-black 을 black으로 바꾸면 해결

여기서 문제는 어떻게 red노드를 A위로 옮기느냐?!

    1. D 의 위치가 red 가 되어야 한다. D를 어떻게 레드로 바꾸냐??

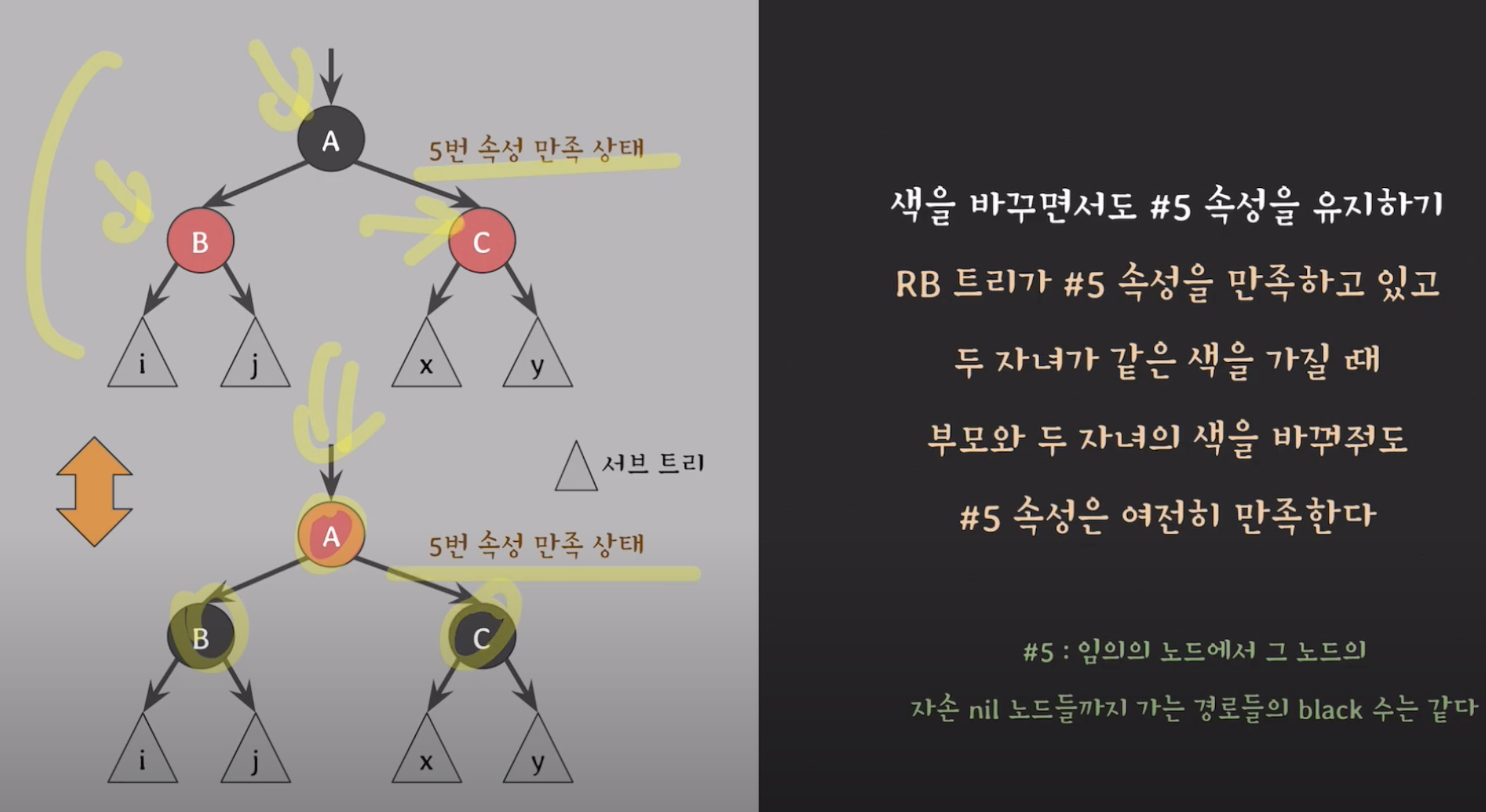
      이 속성을 이용한다.

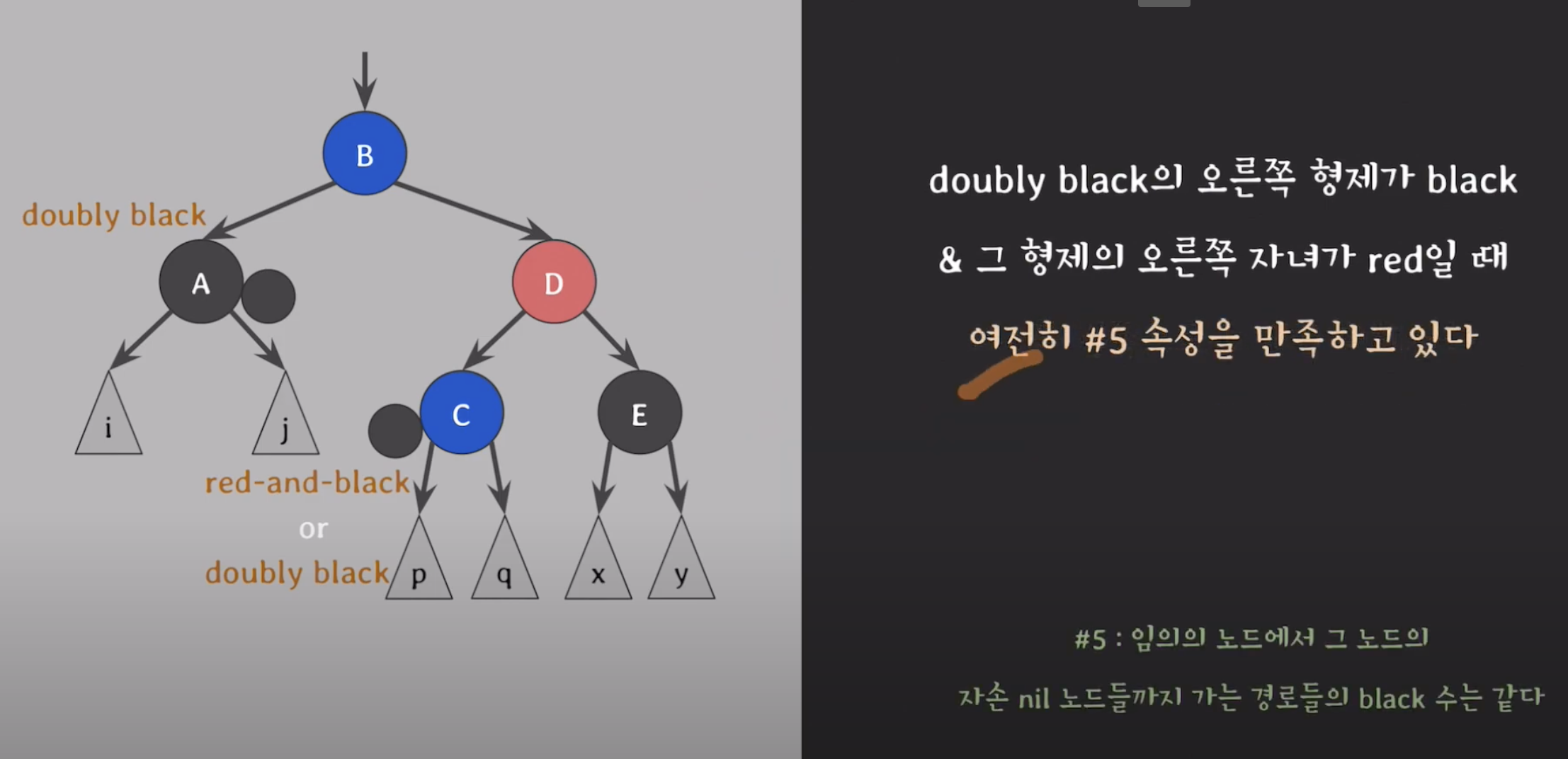
  • C의 색은 모르므로 extra black으로 정의해논다.

그다음 B,D의 색을 바꾸고 왼쪽으로 회전해준다. (B는 빨강,D는 B의색이 된다.)

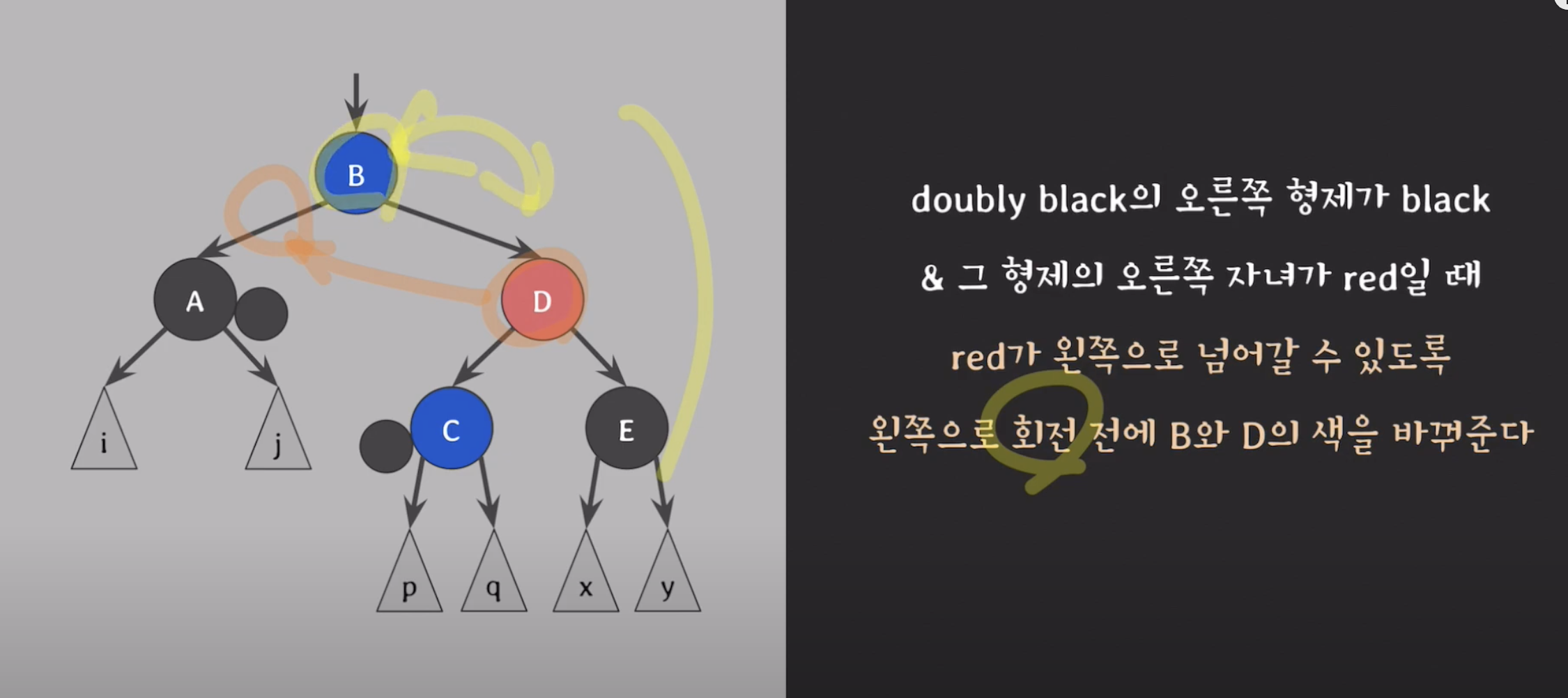
  • 회전후

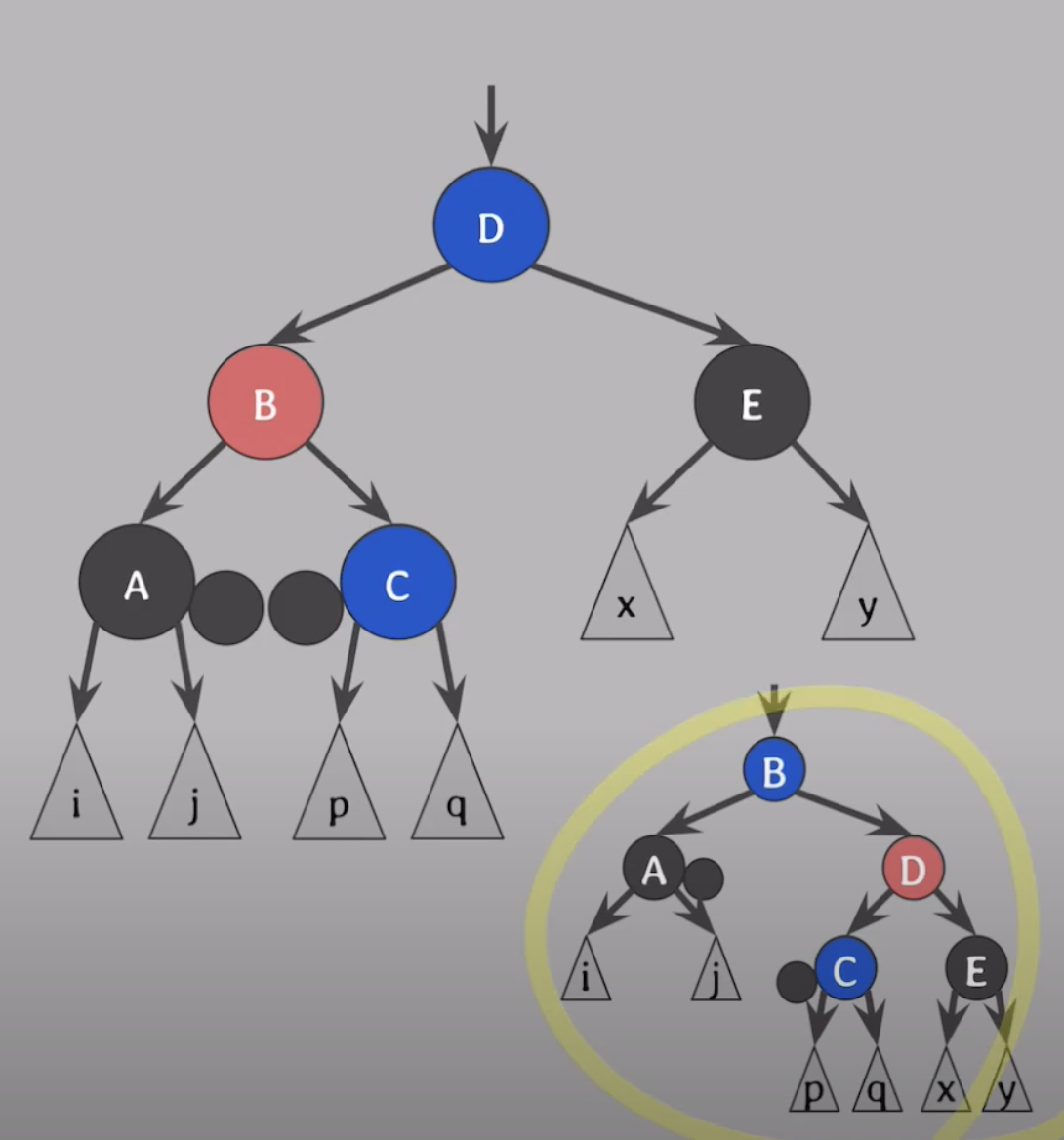
  • A,C의 엑스트라 블랙을 B로 올린다.

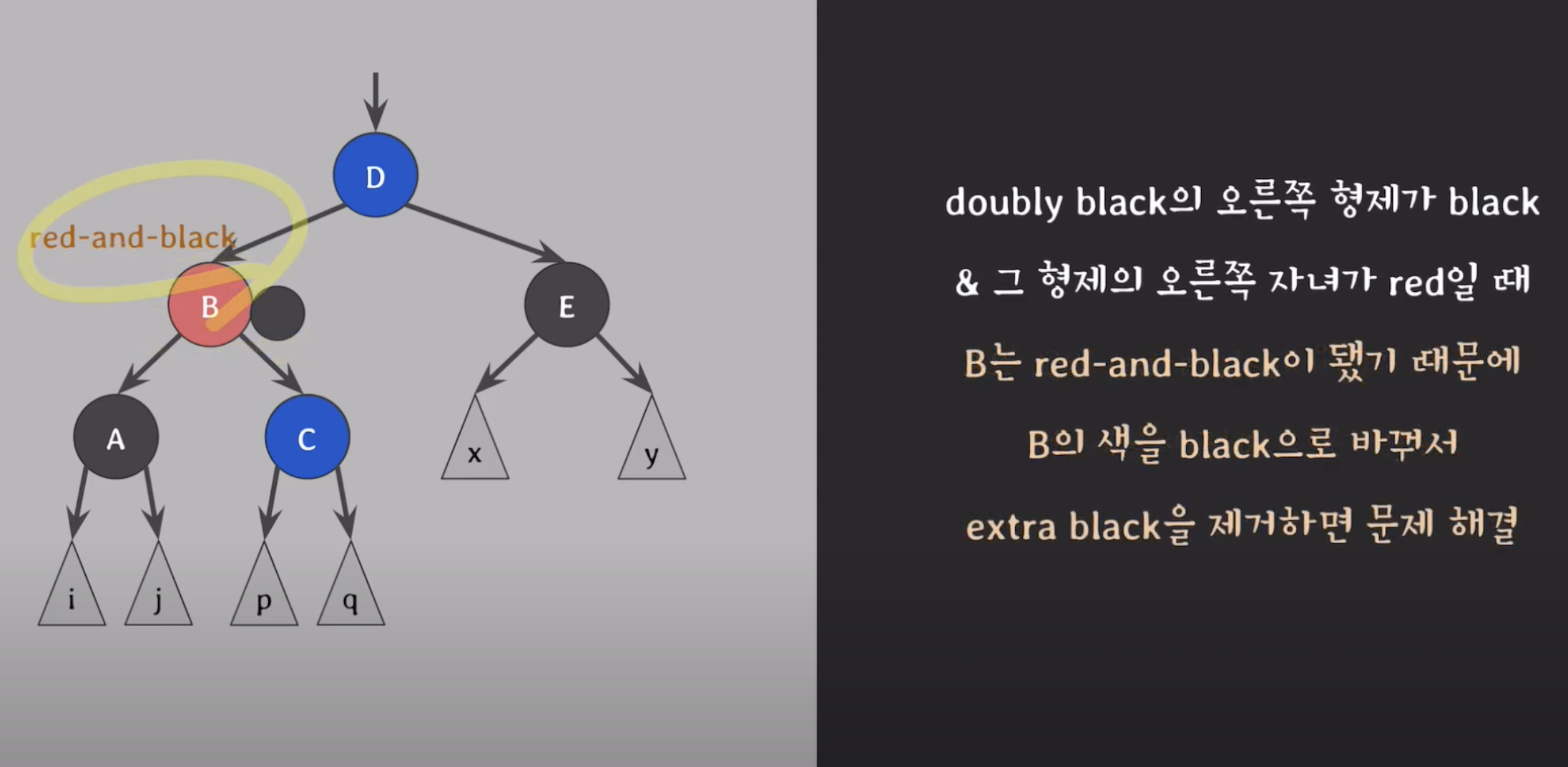
  • red and black 엑스트라 노드를 -> 블랙 으로 바꿔주면 끝!

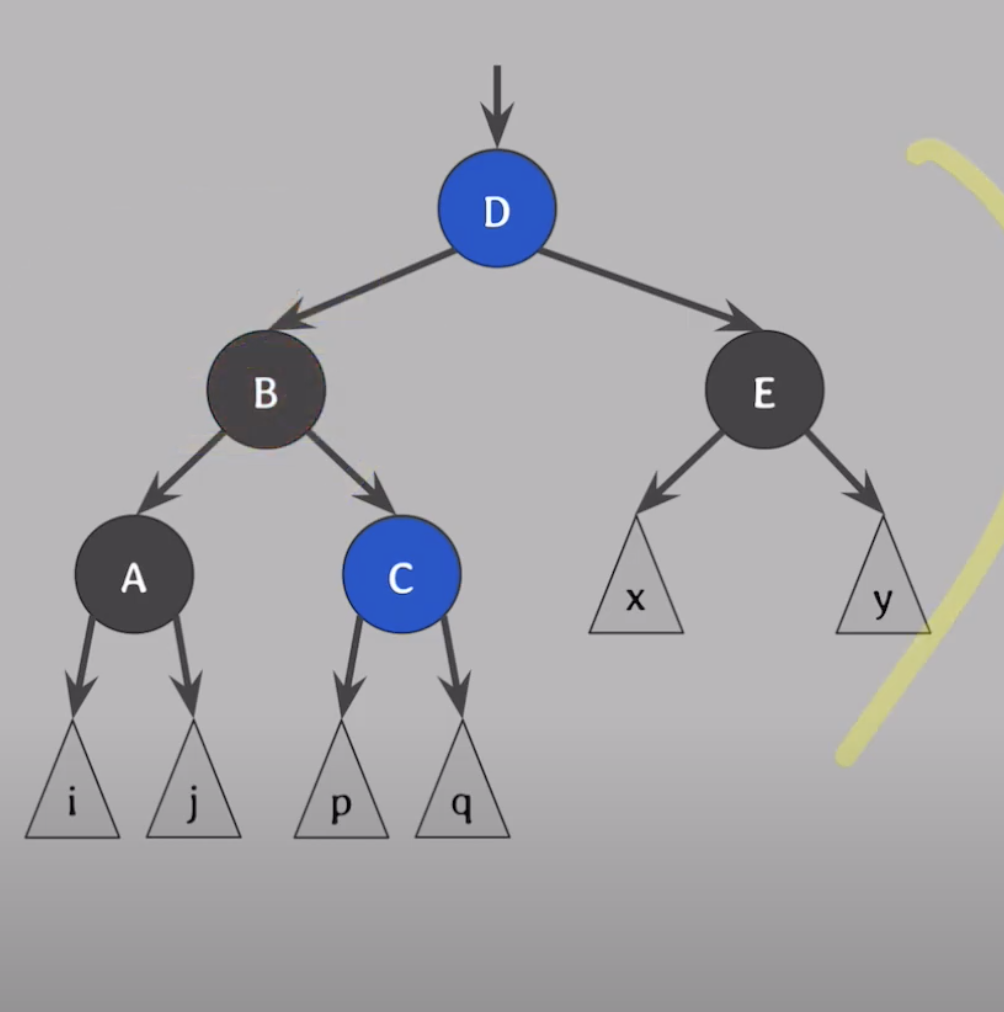
요약 결과론적으로

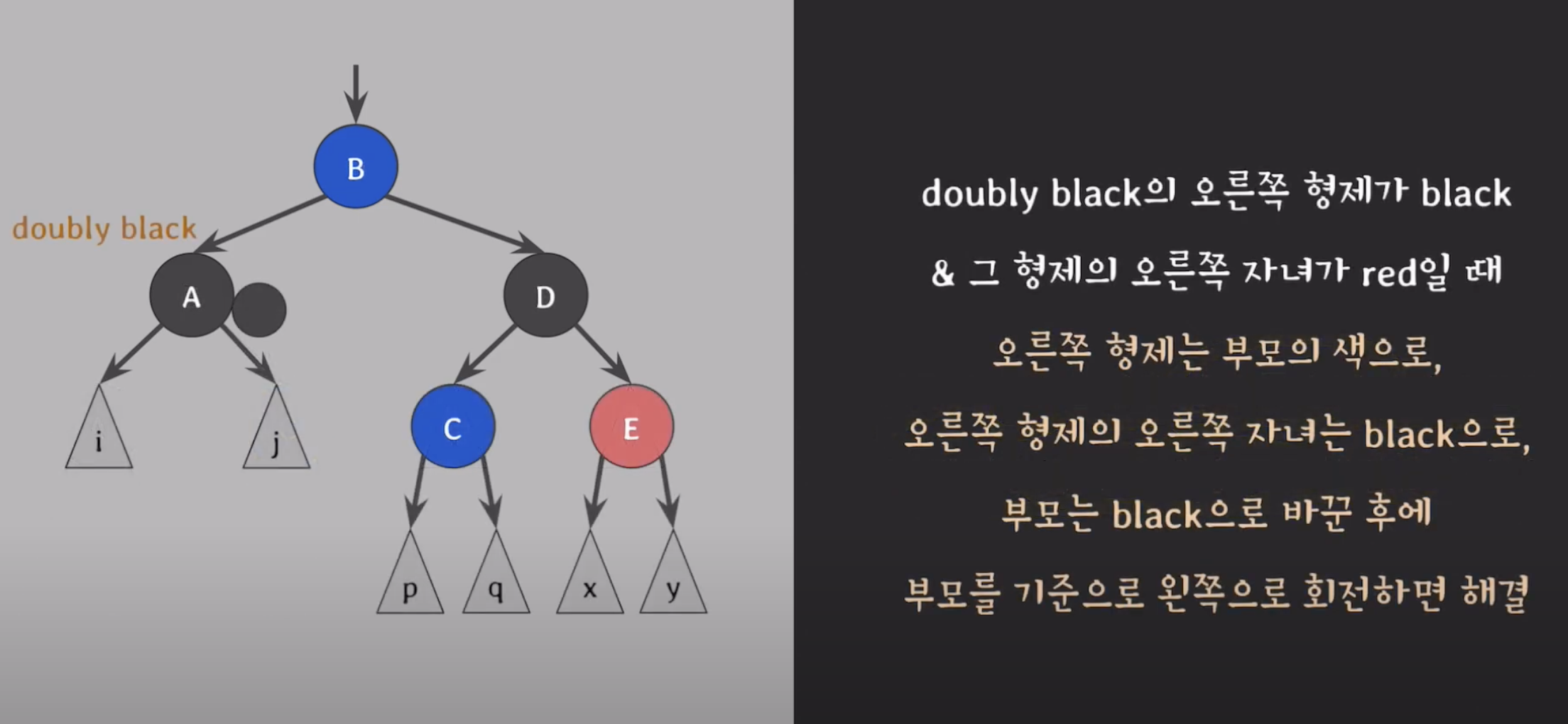
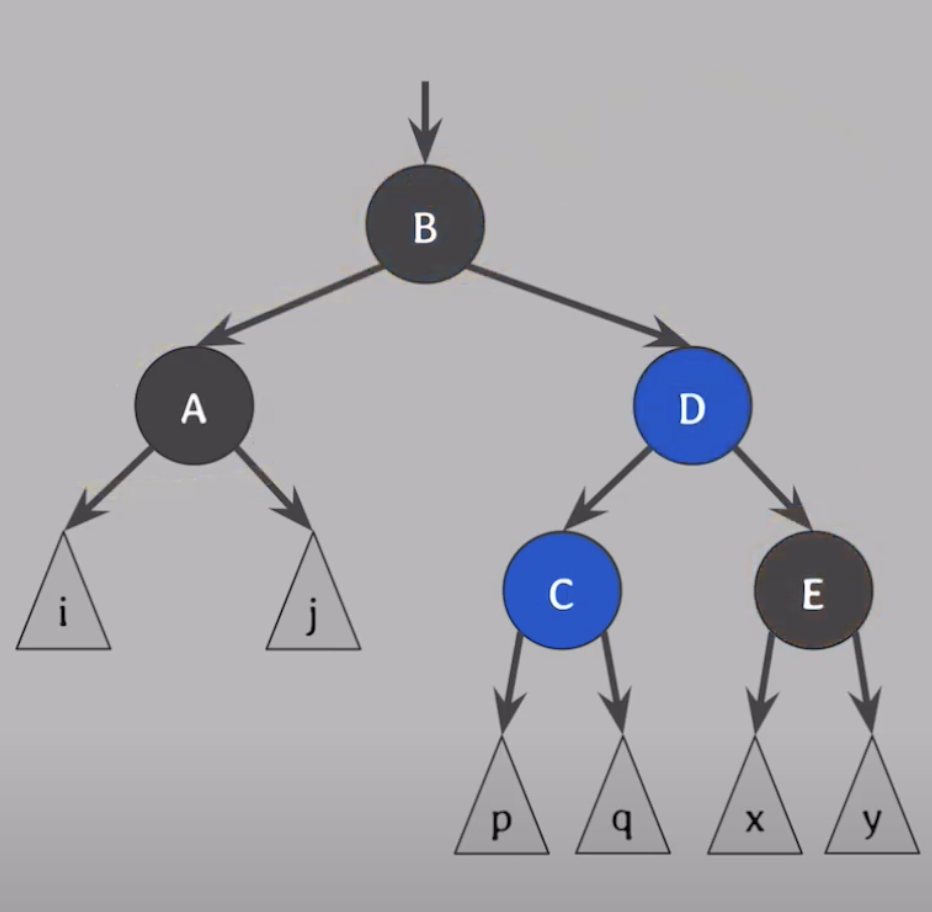
  • B를 기준으로 왼쪽으로 회전 하면 끝 !

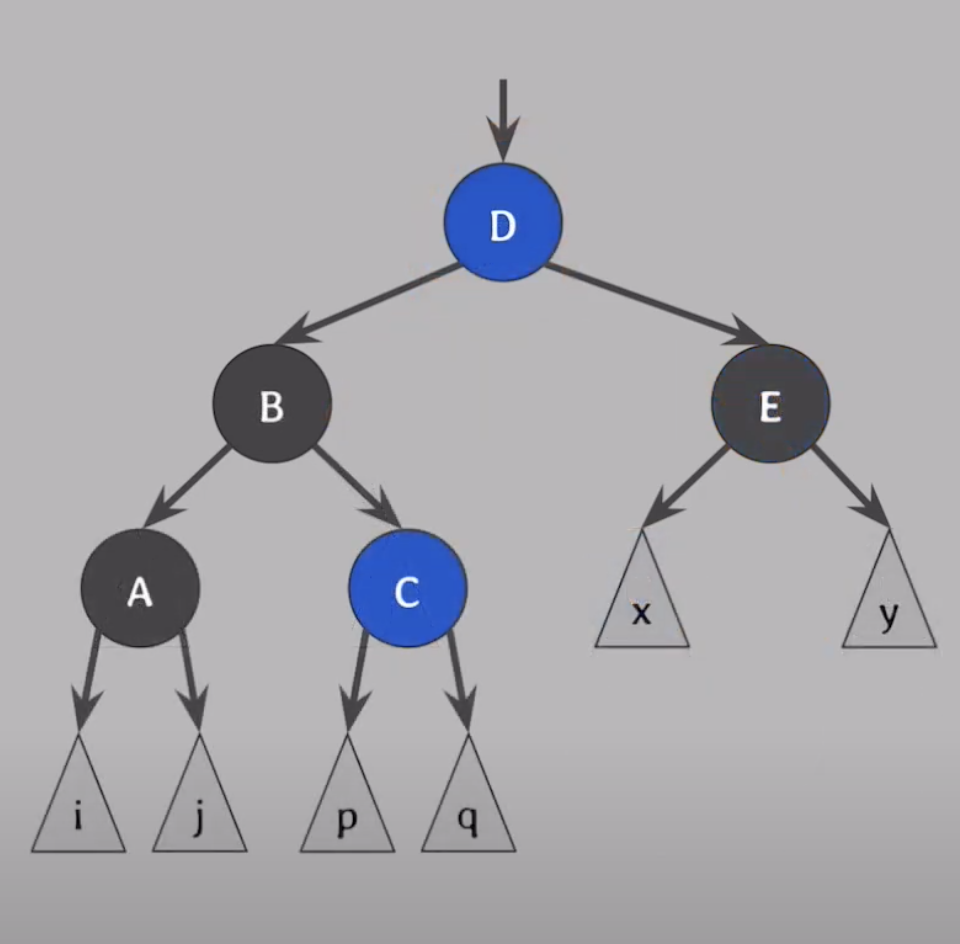
요약의 요약

case 3

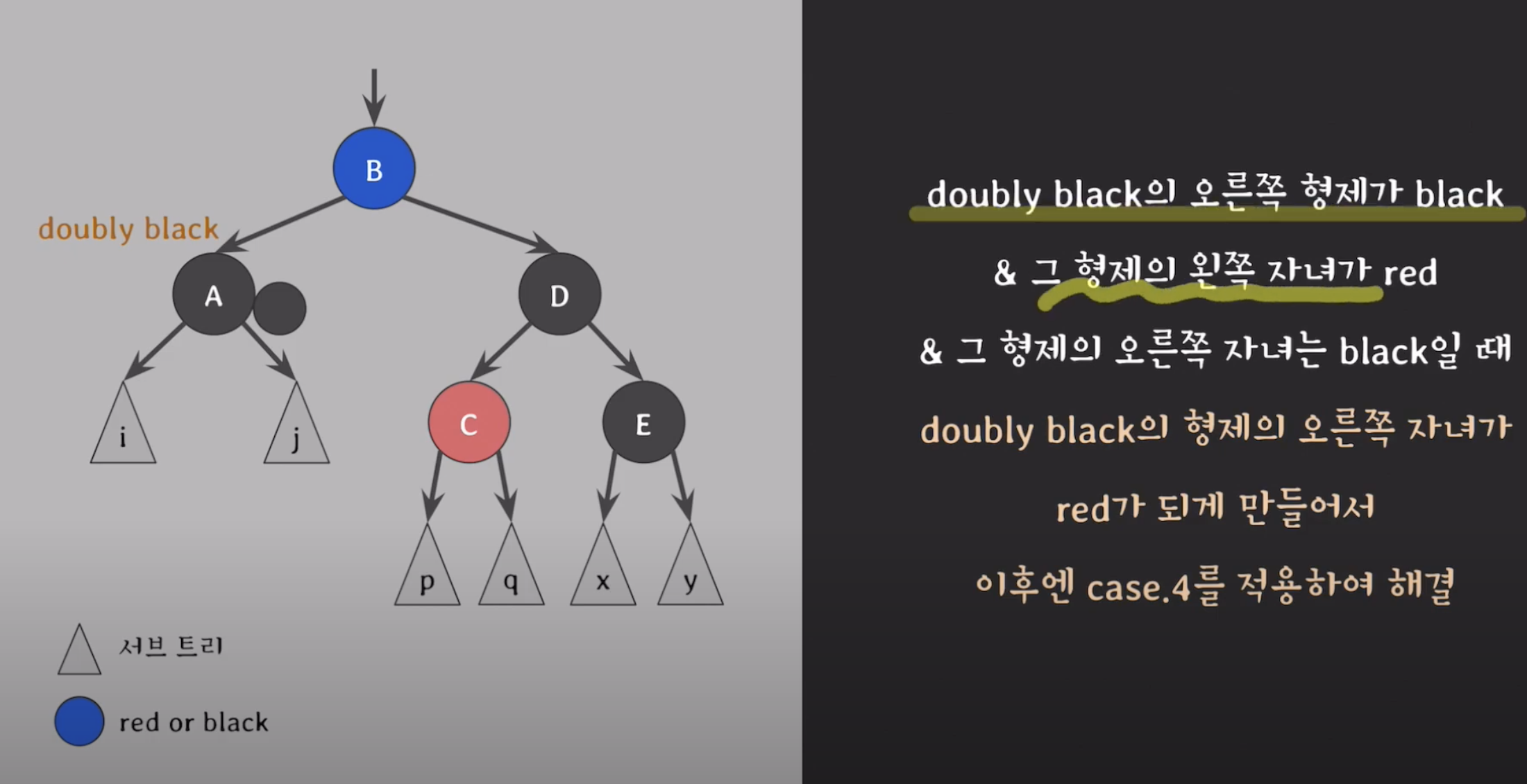
  • C의 빨강을 어떻게 E로 옮겨주냐?
    1.C,D의 색을 바꿔준다
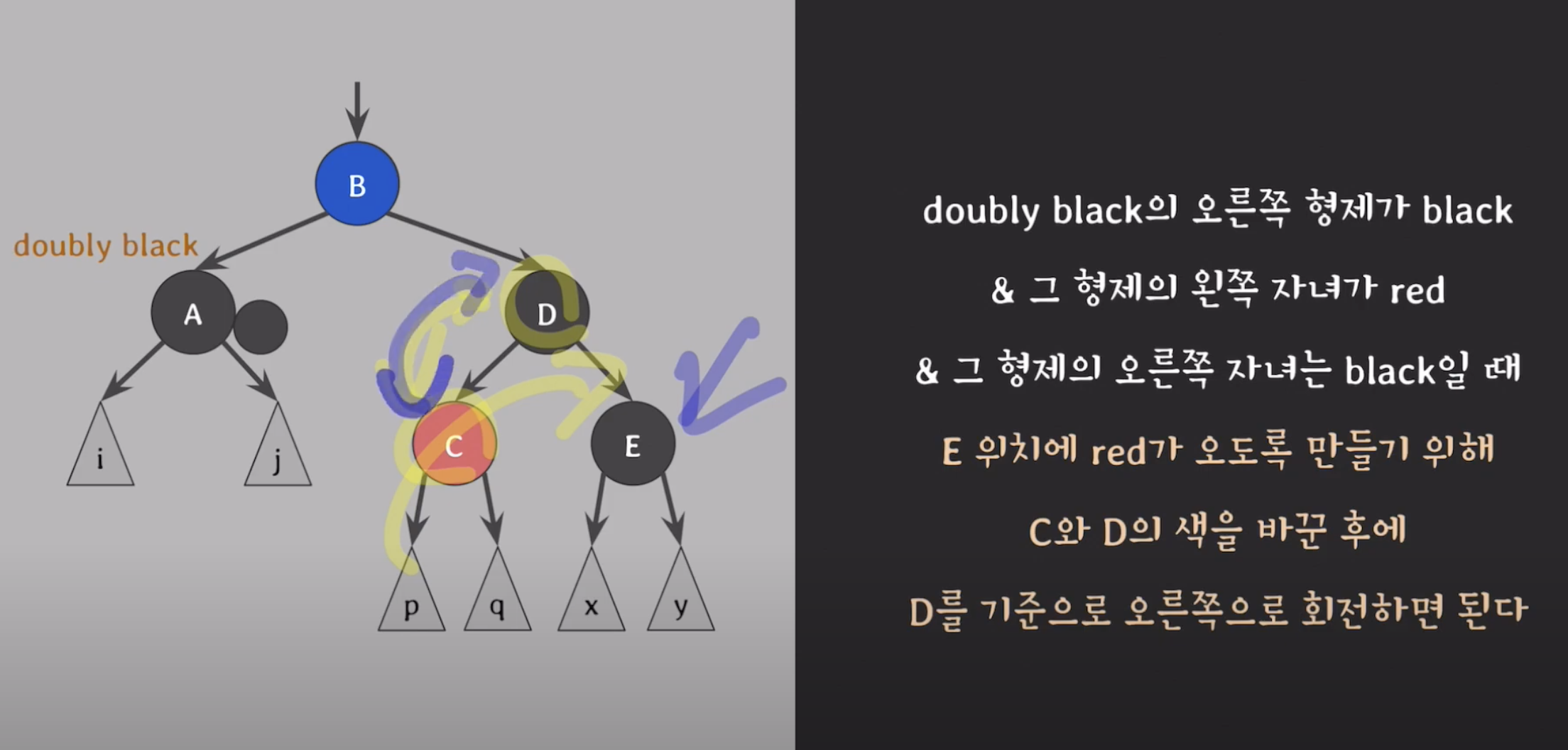
  1. 그리고 D를 기준으로 오른쪽 회전
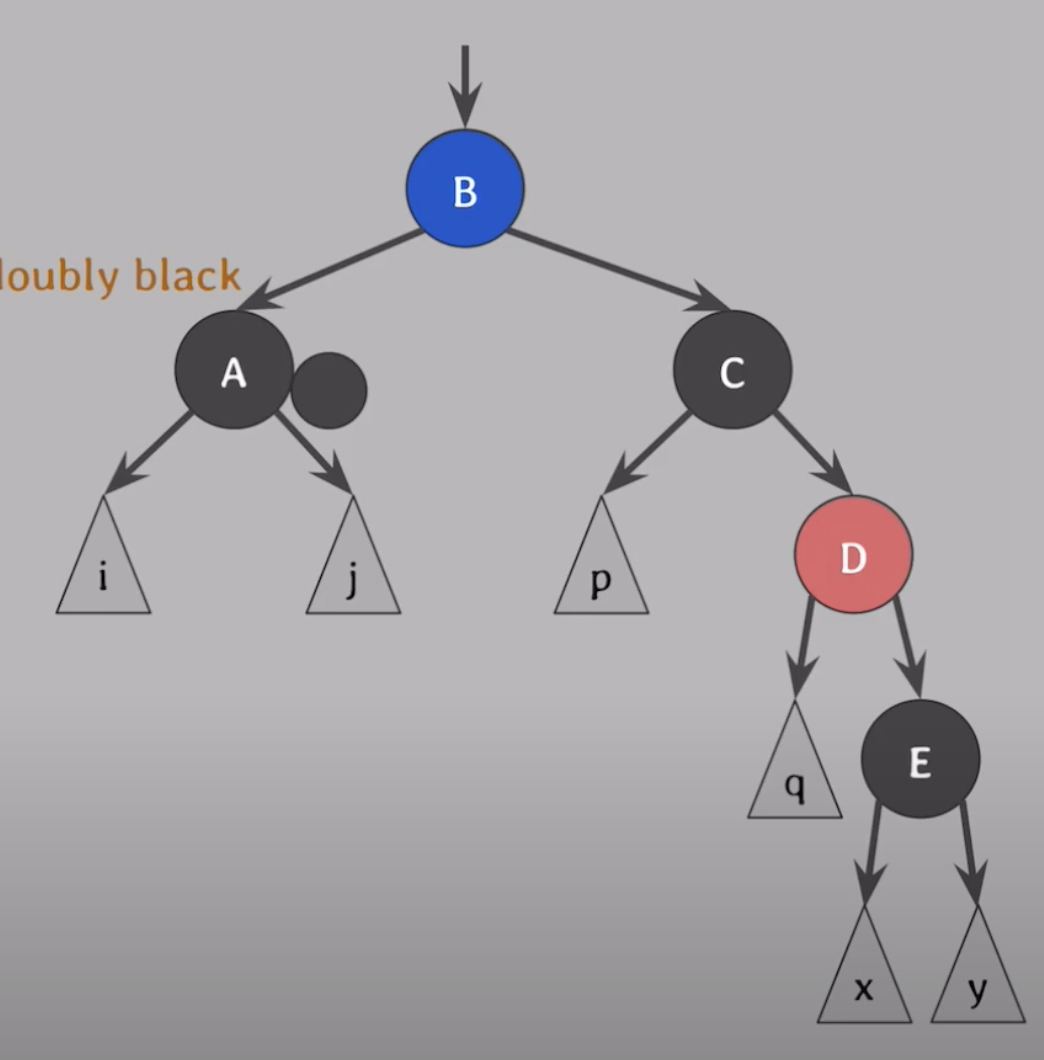
  • 이제 case4 해결 방식으로 해결해 주면 된다.
  • C는 B의 색으로 B와 D는 Black 으로 바꾼후
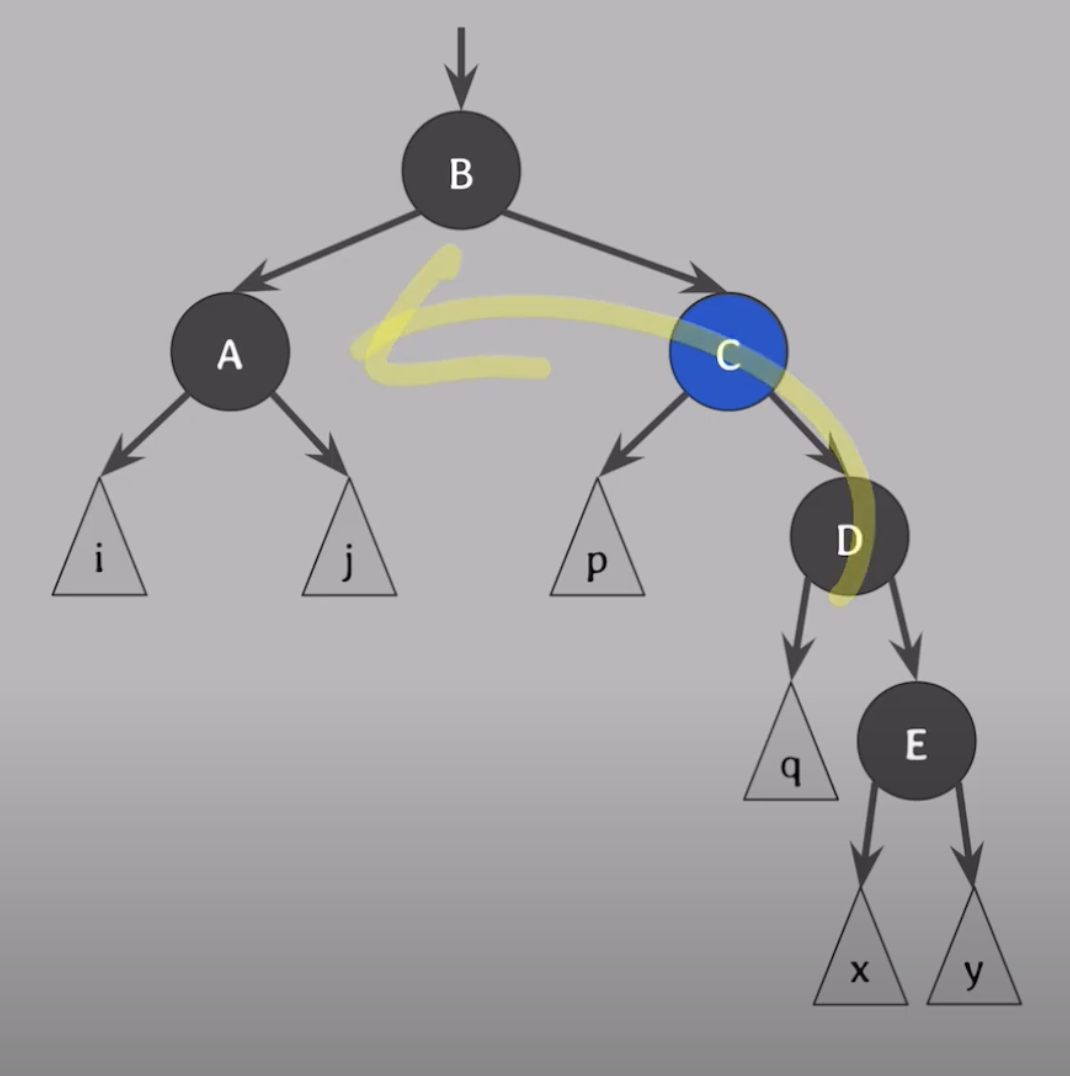
  • B를 기준으로 왼쪽으로 회전

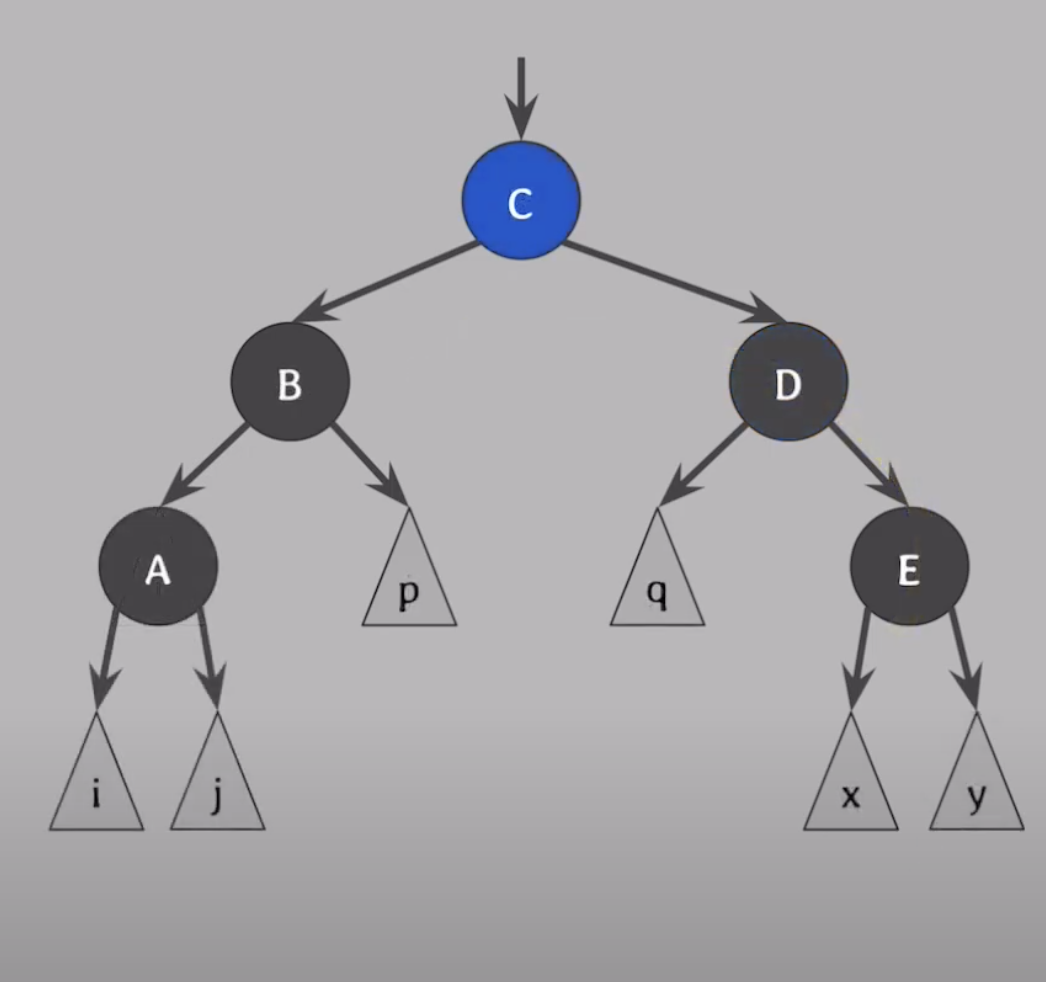
case2

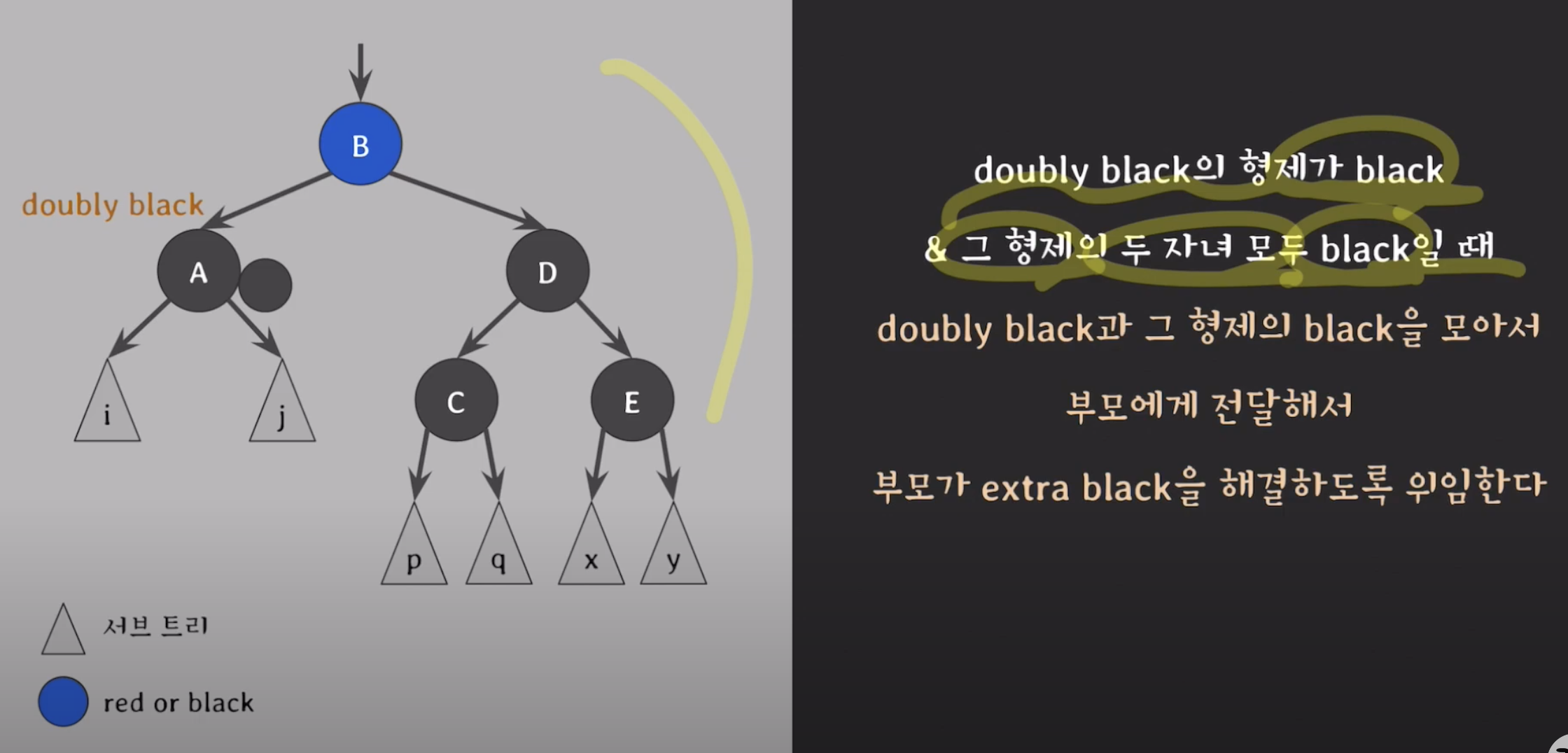
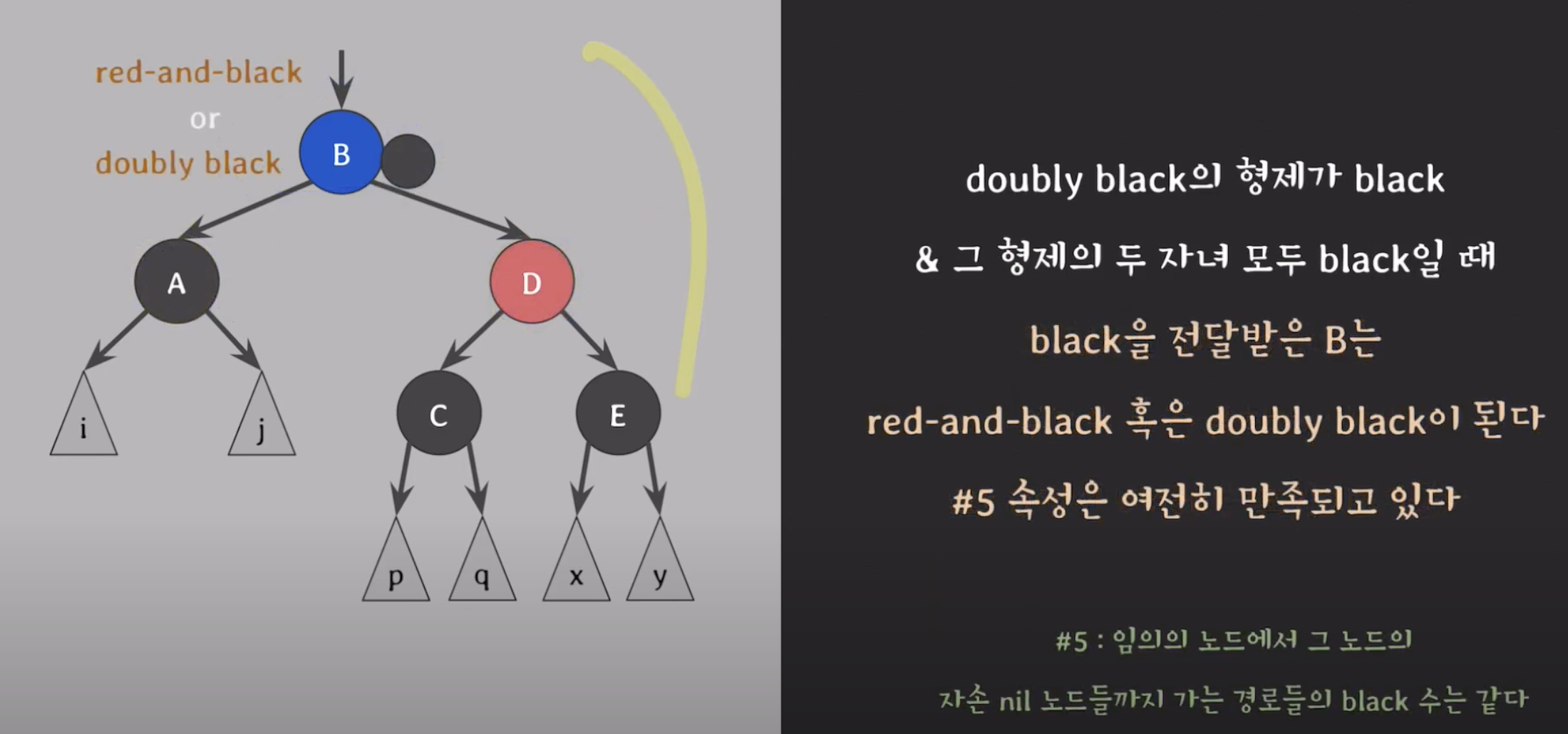
  • 부모 B에 따라 상황에 따라.

case1


요약

코드에 적용 ( extra node 개념은 스킵하고 결과론적으로만 적용)
https://velog.io/@zhy2on/Red-Black-Tree

  • 트리에서 노드를 삭제할 때 없어지는 색을 y_origin_color 라고 한다.
  • 이 origin_color에 따라 fix up 여부가 달라짐.
  • (origin_color가 Black일 때만 fix up이 필요하다. -> 이 때만 Black height이 달라지므로.)

삭제하려는 노드를 z라고 할 때

  • 1-1. z의 자식이 두 명이 아니라면 없어지는 y_color는 z color.
  • 존재하는 z의 자식(둘 다 존재하지 않는다면 leaf node)를 z 자리에 이식. z는 해제
  • 1-2. z의 자식이 두 명이라면 없어지는 y_color는 minimum(z->right) color.
    • minimum(z->right)을 z자리에 이식하기 때문에 결국 사라지는 색은 minimum의 색. (z 자리에 이식할 때 노드색을 z 것으로 물려받는다.)

fix up에 사용할 노드를 x라고 할 때

  • 2-1. z의 왼쪽 자식이 없다면 x는 z->right. z의 오른쪽 자식이 없다면 x는 z->left.
  • 2-2. z의 자식이 두 명이라면 x는 minimum(z->right)->right.
  • minimum은 subtree의 가장 왼쪽 노드이므로 왼쪽 자식이 없음. right가 당연함.

delete fix

case4.
상태
s는 Black, s->right가 Red.

  • s 는 D노드
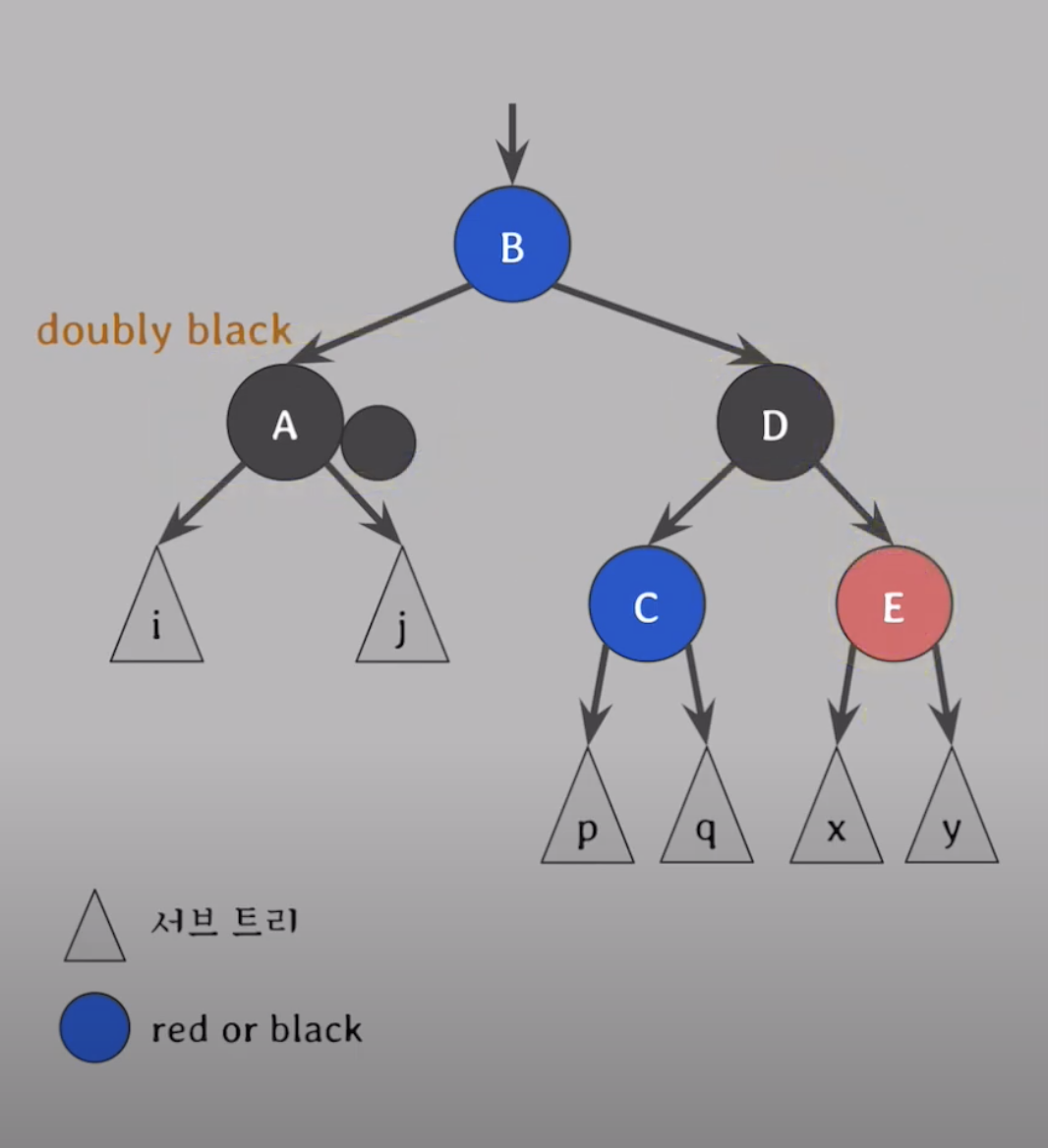
1. s의 color = s->parent color.
2. s->parent, s->right color = ``Black``.
3. s를 기준으로 rotate.

case3.
상태
s는 black. ( s는 D 노드)
s->left 는 red
s->right black

s->right 를 red가 되게 한다음 case4 적용

1. s와 s->left의 color를 바꾼다. (s는 Red로, s->left는 Black으로 바뀜)
2. s->parent를 기준으로 right rotate. (s->parent, 즉 Red가 right child가 된다.)

case2
s는 black
s->left도 블랙
s->right도 블랙

  • s를 red로 바꾸고
  • x->parent 에 fix up 을 위임
    (x = x->parent 로 한 다음 다시 x->parent입장에서 fix up 진행)
1. s->color = Red
2. x = x->parent
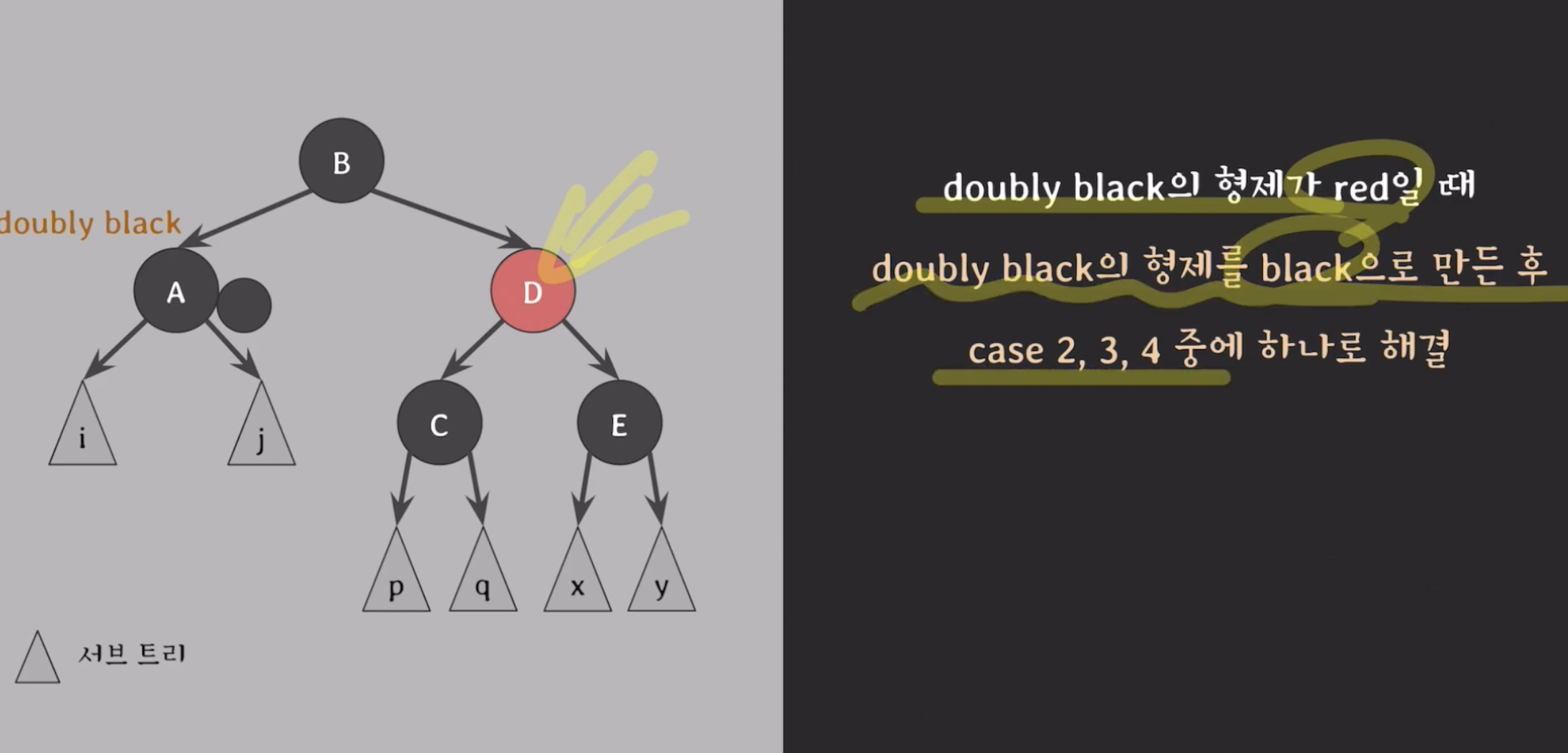
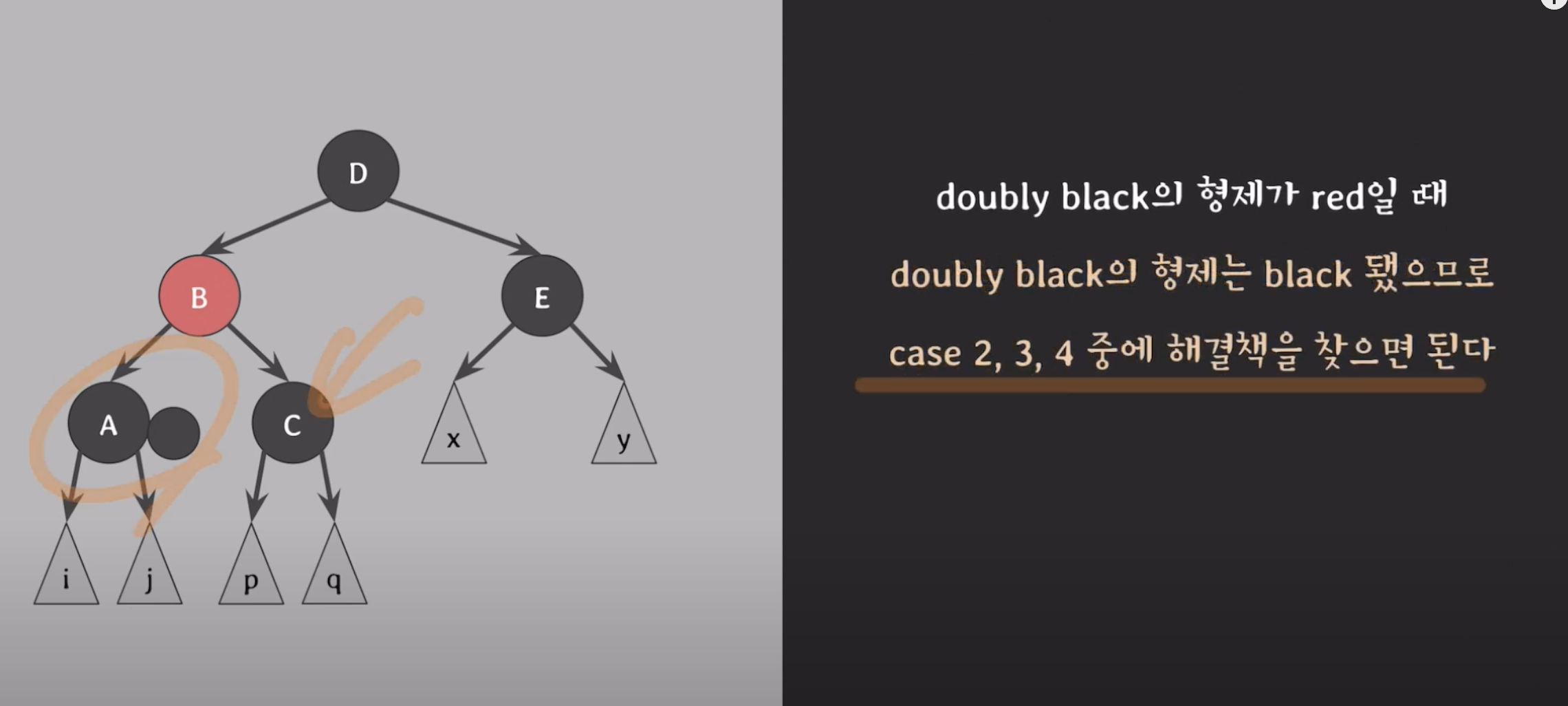
이후 Case 1, Case 2, Case 3, Case 4를 업데이트된 x 입장에서 다시 검사하여 fix up 진행

case1

s가 red

-s 를 레드로 바꾸고
-case 2, 3, 4차례로 검사하면서 fix up 진행.

profile
YP J
be pro
이전 포스트

template 다다시

0개의 댓글