📀 Implementation of Data Input and Output

---

Relational Algebra(관계 대수)

관계 대수는 관계형 데이터베이스에서 원하는 정보와 그 정보를 검색하기 위해서 어떻게 유도하는가를 기술하는 절차적인 언어이다.

• 릴레이션을 처리하기 위해 연산자와 연산규칙을 제공하며, 피연산자와 연산 결과가 모두 릴레이션임
• 질의에 대한 해를 구하기 위해 수행해야 할 연산의 순서를 명시함
• 릴레이션을 조작하기 위한 연산의 집합

Pure Relational operators

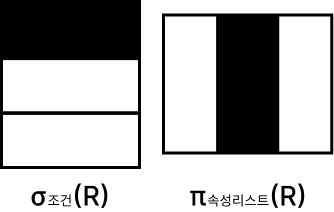
• SELECT : 𝜎
  • 릴레이션에 존재하는 튜플(Tuple) 중에서 선택 조건을 만족하는 튜플의 부분집합을 구하여 새로운 릴레이션을 만드는 연산
  • 릴레이션의 행에 해당하는 튜플을 구하는 것이므로 수형 연산이라고도 함
• PROJECT : 𝜋
  • 주어진 릴레이션에서 속성 리스트(Attribute List)에 제시된 속성 값만을 추출하여 새로운 릴레이션을 만드는 연산
  • 릴레이션의 열에 해당하는 속성을 추출하는 것이므로 수직 연산자라고도 함
• JOIN : ⋈
  • 공통 속성을 중심으로 두 개의 릴레이션을 하나로 합쳐서 새로운 릴레이션을 만드는 연산
  • JOIN의 결과는 Cartesian Product(교차곱)를 수행한 SELECT를 수행한 것과 같음
• DIVISION : ÷
  • X⊃Y인 두 개의 릴레이션R(X)와 S(Y)가 있을 때, R의 속성이 S의 속성값을 모두 가진 튜플에서 S가 가진 속성을 제외한 속성만을 구하는 연산

Generic Set operators

• UNION(합집합) : ∪
  • 두 릴레이션에 존재하는 튜플의 합집합을 구하되, 결과로 생성된 릴레이션에서 중복되는 튜플은 제거되는 연산
  • 합집합의 Cardinality(튜플의 수)는 두 릴레이션의 카Cardinality의 합보다 크지 않다.
• INTERSECTION(교집합) : ∩
  • 두 릴레이션에 존재하는 튜플의 교집합을 구하는 연산
  • 교집합의 Cardinality(튜플의 수)는 두 릴레이션 중 Cardinality가 적은 릴레이션의 Cardinality보다 크지 않다.
• DIFFERENCE(차집합) : −
  • 두 릴레이션에 존재하는 튜플의 차집합을 구하는 연산
  • 차집합의 Cardinality(튜플의 수)는 릴레이션 R의 Cardinality보다 크지 않다.
• CARTESIAN PRODUCT(교집합) : ×
  • 두 릴레이션에 있는 튜플들의 순서쌍을 구하는 연산
  • 교찹곱의 Degree(속성의 수)는 두 릴레션의 Degree를 더한 것과 같고, Cardinality(튜플의 수)는 두 릴레이션의 카디널리티를 곱합 것과 같음
  • 예) 릴레이션 R의 차수(Degree) 3, 카디널리티(Cardinality) 3, 릴레이션 S의 차수(Degree) 4, 카디널리티(Cardinality) 4일 때, 두 릴레이션을 카티션 프로턱트(CARTESIAN PRODUCT)한 결과 릴레이션의 차수와 카디널리티를 구하시오.
    차수 : 3 + 4 = 7, 카디널리티 : 3 x 4 = 12

Relational Calculus(관계 해석)

관계 해석은 관계 데이터의 연산을 표현하는 방법이다.

• 관계 데이터 모델의 제안자 코드(E. F. Codd)가 수학의 술어 해석(Predicate Calculus)에 기반을 두고 관계 데이터베이스를 위해 제안함
• 원하는 정보가 무엇이라는 것만 정의하는 비절차적 특성을 지님
• 원하는 정보를 정의할 때는 계산 수식을 사용
• 튜플 해석식을 사용하는 튜플 관계 해석과 도메인 해석식을 사용하는 도메인 관계 해석으로 구분됨

Anomaly(이상)

이상이란 데이터베이스 내에 데이터들이 불필요하게 중복되어 릴레이션 조작 시 예기치 않게 발생하는 곤란한 현상을 의미한다.

• 삽입 이상(Insertion Anomaly) : 데이블에 데이터를 삽입할 때 의도와는 상관없이 원하지 않는 값들로 인해 삽입할 수 없게 되는 상황
• 삭제 이상(Deletion Anomaly) : 데이블에서 튜플을 삭제할 때 의도와는 상관없는 값들도 함께 삭제되는, 즉 연쇄 삭제가 발생하는 현상
• 갱신 이상(Update Anomaly) : 테이블에서 튜플에 있는 속성 값을 갱신할 때 일부 튜플의 정보만 갱신되어 정보에 불일치성(Incosistency)이 생기는 현상

Functional Dependency(함수적 종속)

• Functional Dependency(함수적 종속) : 어떤 테이블 R에서 X와 Y를 각각 R의 속성 집합의 부분집합이라 하면, 속성 X의 값 각각에 대해 시간에 관예없이 항상 속성 Y의 값이 오직 하나만 연관되어 있을 때 Y는 X에 함수적 종속 또는 X가 Y를 함수적으로 결정한다고 하며, X → Y 로 표기
• Full Functional Dependency(완전 함수적 종속) : 어떤 테이블 R에서 속성 Y가 다른 속성 집합 X 전체에 대해 함수적 종속이면서 속성 집합 X의 어떠한 진부분 집합 Z(Z ⊂ X)에도 함수적 종속이 아닐 때, 속성 Y는 속성 집합 X에 완전 함수적 종속이라고 함
  • 예를 들어, 주민번호를 가지고 나를 특정할 수 있는 것처럼 특정한 키를 가지고 나를 특정할 수 있는 것을 말함.
• Partial Functional Dependency(부분 함수적 종속) : 어떤 테이블 R에서 속성 Y가 다른 속성 집합 X 전체에 대해 함수적 종속이면서 속성 집합 X의 임의의 진부분 집합에 대해 함수적 종속일 때, 속성 Y는 속성 집합 X에 부분 함수적 종속이라고 함
  
• Transitive Functional Dependency(이행적 함수적 종속) :
  X → Y이고 Y → Z일 때 X → Z를 만족하는 관계를 의미

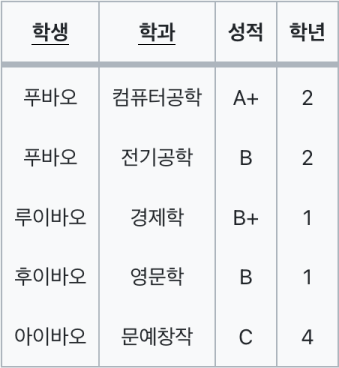
(테이블 <R>의 속성 '학생'과 '학과'의 밑줄은 키를 의미.)

• 테이블 <R>은 '성적' 기본키인 {학생, 학과}에 대해 Full Functional Dependency.
• 테이블 <R>에서 '학년'은 기본키인 {학생, 학과} 중 '학생'만으로 식별이 가능하므로 기본키에 대해 Partial Functional Dependency.

---

참고,
길벗알앤디. 『정보처리기사 실기 단기완성』. 길벗. 2023.