선형 회귀_이해하기_Intro

[목차]

선형회귀

가설

손실

경사하강법

실습

1. 선형회귀란? (Linear Regression)

선형회귀(Linear Regression)란 머신러닝의 지도학습 방식 중 하나인 대표적인 회귀알고리즘입니다. 여기서 지도학습이란, 입력값(x)이 주어지면, 해당 입력값에 대한 라벨(y)값을 주어 학습시킴으로써 f(x)함수를 찾아내는 작업을 의미합니다.

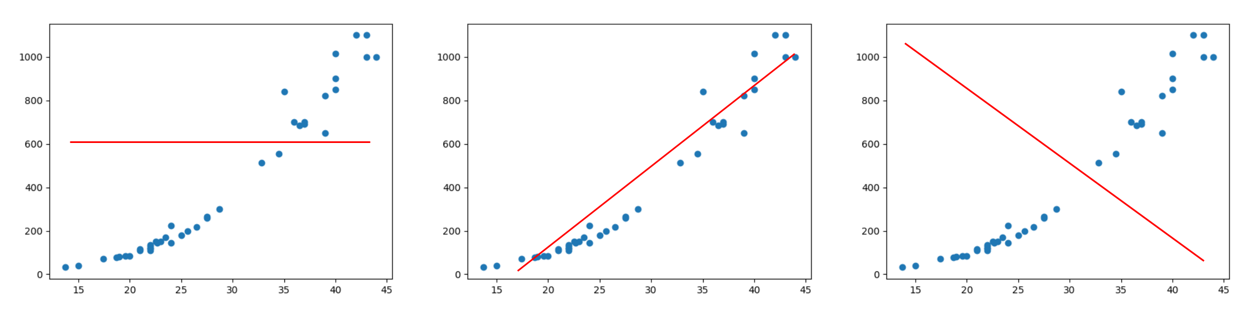
이미지 출처 : https://rebro.kr/185

위의 그래프에서 파란색 점들은 입력값과 라벨값인 (x,y)인데, 파란색 점들이 어느정도 연속성 및 규칙성이 있는 것을 확인할 수 있습니다.

파란색 점들로부터 특정 규칙 즉,함수 f(x)를 찾아내려고 할 때, 위 세 그래프 중 어떤 빨간 선이 가장 적합한 f(x)라고 할 수 있을까요?

대부분의 사람들은 직관적으로 중간에 있는 그래프의 빨간 선이 정답이라는 것을 알 수 있을텐데요. 왜 중간에 있는 그래프가 가장 적합한 f(x)인지에 대해 천천히 알아봅시다.

2. 가설이란? (Hypothesis)

위에서 언급했듯이, 지도학습이란 입력값(x)에 라벨값(y)를 붙인 값들을 모아서 훈련시킨 다음, 이 데이터 집합으로부터 하나의 함수를 유추하는 방식입니다.

흔히 x를 독립 변수, y를 종속 변수라고 하는데요.
x값이 1개인 (단순 선형 회귀) 방식에서는 그 수식을

y=Wx+b

라고 표현하는데, 여기서 W는 가중치(weight), b는 편향(bias)를 나타냅니다. 위에 3개의 그래프에서는 y=Wx+b, 즉 가설로 나타낸 것이 빨간선입니다.
따라서 우리가 선형회귀모델 함수를 훈련하는 것은 즉, 적합한 W와 b의 값을 찾기 위한 과정이라고 할 수 있습니다.

3. 손실이란? (Loss)

그렇다면 적합한 W와 b의 값이란 도대체 그 기준이 무엇이며 어떻게 설정할 수 있을까요?

결론부터 얘기하면 "평균적인 오차" 를 최소화하는 W와 b의 값이 가장 적합한 값이라고 할 수 있습니다.

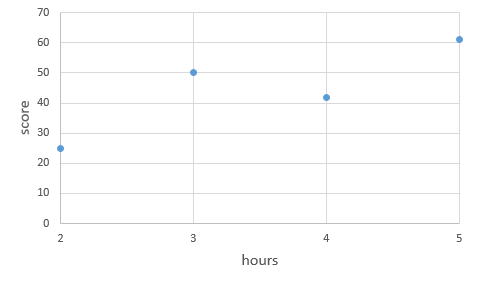
이미지 출처:https://wikidocs.net/53560

여기 파란색 점으로 표시된 (x,y)의 데이터셋들과, y = 13x+ 1 로 그린 주황색 직선이 있습니다.

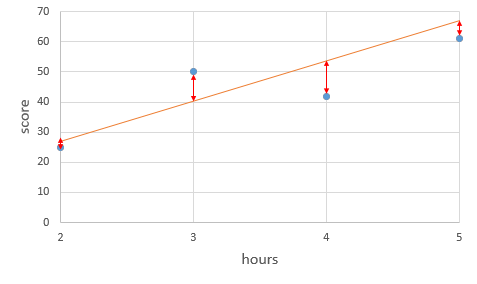
이미지 출처:https://wikidocs.net/53560

주황색 선분이 적합한 선형회귀 모델인지 탐색하기 위해서는 오차값을 우선 구해야 합니다. hours값을 기준으로 오차값은 순서대로 (-2, 10, -9, -5)
입니다.



이처럼 오차값은 양수와 음수 모두 나올 수 있기 때문에, 일반적인 평균을 구하는 공식 대신에 다음과 같이 각 오차값에 제곱을 해준 값을 모두 더한 다음, 데이터 개수로 나누는 공식을 사용하는데 이를 MSE(Mean Squared Error)라고 합니다.

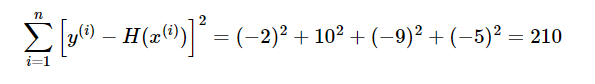
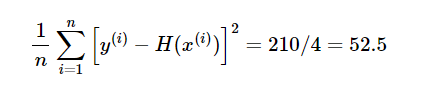
이미지 출처:https://wikidocs.net/53560

각 오차값(-2, 10, -9, -5)을 제곱한 값들의 합은 210이고, 총 데이터의 개수는 4개 이므로, y = 13x + 1 식의 평균 제곱 오차의 값은 52.5입니다. 훈련데이터값을 가장 잘 나타내는 직선을 구하기 위해서는 방금 구한 평균 제곱 오차(MSE)의 값이 최소가 되어야 합니다.

적절한 W와 b의 값 = MSE의 최솟값

4. 경사하강법이란? (Gradient Descent)

그럼 이제 평균 제곱 오차(MSE)의 최솟값을 구하는 방법에 대해 알아보겠습니다. 이 때 사용되는 것이 옵티마이저(Optimizer) 알고리즘이라고 하는데, 그 중 가장 기본적인 방법인 경사하강법(Gradient Descent)에 대해 알아보겠습니다.

경사하강법도 이론 그 자체는 생각보다 어려운 내용은 아닙니다.
일단, 설명의 편의를 위해 편향(b)를 제외하고, H(x)=Wx라고 가정하겠습니다. 그리고 비용함수=손실함수는 cost라고 표기합니다.

이미지 출처:https://wikidocs.net/53560

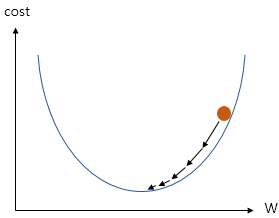
위의 그래프는 가장 cost값이 낮은 지점을 찾기 위해 W값의 변화를 주고 있는 그림입니다.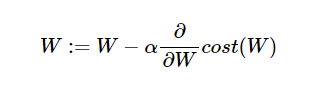

이미지 출처:https://wikidocs.net/53560

그리고 위의 수식은, 최저 cost값을 구하기 위한 W값의 조정함수 입니다.
어려워 보이지만 간단한 개념인데요

(1) 기울기가 양수인 경우 W값을 줄이고 (왼쪽으로 이동)
(2) 기울기가 음수인 경우 W값을 늘린다 (오른쪽으로 이동)

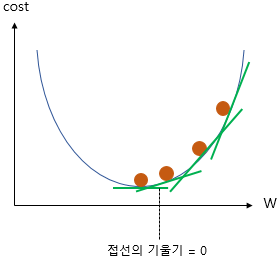
이렇게 수식을 통해 W값을 조정함으로써 접선의 기울기가 0이 되는 지점,
즉, cost비용이 최저가 되는 지점을 찾을 수 있게 됩니다.

5. Pytorch 실습

1. 셋팅

import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim

torch.manual_seed(1)

위와 같이 seed값을 준 이유는 나중에 해당 코드를 재실행할 때 동일한 seed값의 경우 같은 값을 얻을 수 있기 때문이다.

2. 변수 선언

x_train = torch.FloatTensor([[1], [2], [3], [4]])
y_train = torch.FloatTensor([[7], [14], [21], [28]])

x와 y의 값을 선언했습니다.

3. W와 b의 값 0으로 초기화

W = torch.zeros(1, requires_grad=True) 
b = torch.zeros(1, requires_grad=True)

가중치(W)와 편향(b)를 모두 0으로 초기화 설정했습니다.
따라서 현재 직선의 방정식은 y= 0*x + 0 와 같은 형태입니다.

4. 가설과 비용함수 설정

#H(x)=Wx+b
hypothesis = x_train * W + b   

#MES
cost = torch.mean((hypothesis - y_train) ** 2) 

5. 경사하강법 구현

optimizer = optim.SGD([W, b], lr=0.01)

위의 SGD는 경사하강법의 일종이고, lr는 학습률을 의미합니다.

학습률이 너무 높은 경우 cost값의 최저점을 찾지 못하고 발산하는 경우가 있으며, 또 너무 낮은 경우 학습 시간이 오래 걸린다는 단점이 있으므로 적당한 lr값을 설정하는 것이 중요합니다.

# gradient를 0으로 초기화
optimizer.zero_grad() 

# 비용 함수를 미분하여 gradient 계산
cost.backward() 

# W와 b를 업데이트
optimizer.step() 

그리고 cost의 최저값을 찾기 위해 위와 같이 w,b값을 업데이트하며 조정하는 과정을 거칩니다.

nb_epochs = 1999 
for epoch in range(nb_epochs + 1):

    hypothesis = x_train * W + b
    cost = torch.mean((hypothesis - y_train) ** 2)

    optimizer.zero_grad()
    cost.backward()
    optimizer.step()

    if epoch % 100 == 0:
        print('Epoch {:4d}/{} W: {:.3f}, b: {:.3f} Cost: {:.6f}'.format(
            epoch, nb_epochs, W.item(), b.item(), cost.item()
        ))

해당 코드를 실행했을 때

W=6.998 , b=0.007로
y=7*x 함수에 거의 근접한 것을 확인할 수 있습니다.