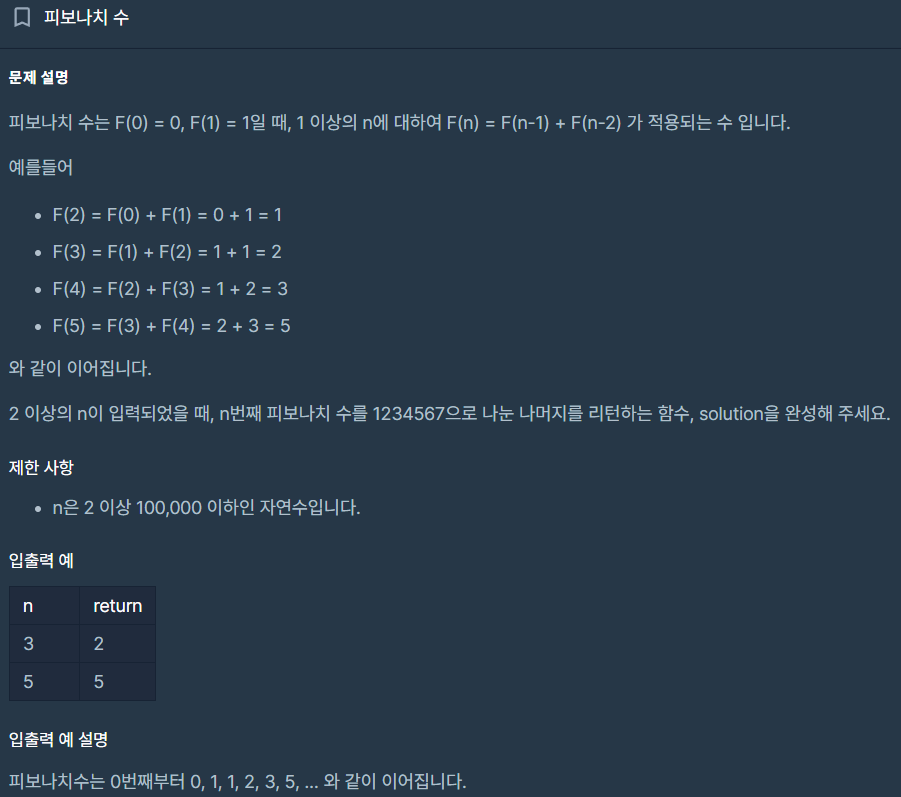
문제

프로그래머스 문제링크

풀이 코드

class Solution {
    public int solution(int n) {

        int answer[] = new int[n+1];
        answer[0] = 0;
        answer[1] = 1;
        for (int i = 2; i <= n; i++)
        {
            int sum = answer[i - 2] + answer[i - 1];
            answer[i] = sum % 1234567;
        }
        return answer[n];
    }
}

리뷰

1. 피보나치 수F(n) = F(n-2) + F(n-1)에 대한 문제입니다.
2. n은 2 이상이라는 조건이 있음으로 문제를 풀때 default값으로 answer[0] = 0, answer[1] = 1을 줌으로 피보나치 수를 계산할 것입니다.
3. n을 기반으로 동적할당을 하여 피보나치 수를 저장할 배열을 만들어줍니다.
   3-1. n+1인 이유 : index는 0번부터 시작하기 때문에 +1을 해주었습니다.
4. 반복문을 통해 피보나치 수열의 세 번째 원소부터 n까지 계산을 반복합니다.
   4-1. sum을 통해 피보나치 수열을 계산하여 줄 것이며, 피보나치 수열의 정의에 따라 F(n) = F(n-2) + F(n-1)을 만족하게 하였습니다.
   4-2. 문제에서 n은 100000이하의 자연수 이기때문에 int 범위를 초과하고도 넘칩니다.
   4-3. n = 48일 경우에 int범위인 2147483647을 넘어가기 때문에 오버플로우가 발생하게 됩니다.
   4-4. 이 문제를 해결하기 위해서는 BigInteger를 사용하면 해결되지만 문제에서 1234567을 나누어줌으로 계산할 수 있는 범위를 주었습니다.
   4-5. 1234567을 나누게 되면 1234567미만의 숫자는 나머지가 자신을 포함하게 됩니다.
5. n = 31일 경우 피보나치 수열의 값은 832040 이며, 1234567을 나누어주어도 나머지 값이 832040임으로 그 값을 그대로 반환하게 됩니다.
   5-1. n = 32일 경우 피보나치 수열의 값은 1346269 이며, 1234567을 나누어주면 그 값을 초과하기 때문에 나머지 값인 111702을 반환하게 됩니다.
   5-2. 위와 같은 케이스가 맞는지 프로그래머스 테스트케이스 9번을 확인하여 아래에 첨부하였습니다.
6. int 범위에서 오버플로우가 발생하지 않도록 만든 answer[n]을 반환하여 문제를 마치게 됩니다.

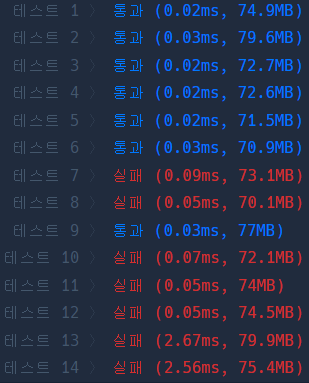
프로그래머스 테스트 케이스 9번

1. 테스트를 함에 있어 테스트 7~14번은 인트범위를 초과하는 값을 가지고 있는것을 확인하였습니다.
2. 테스트 7~14번중 제일 낮은 피보나치 수는 테스트 케이스 9번이었습니다.
3. 테스트 케이스 9번의 경우 n = 358 인 것을 확인하였고 이를 1234567로 나누어 보았습니다.

import java.math.BigInteger;
public class test1
{
   public static void main(String[] args)
    {
        // 큰 수
        String bigNumber = "293825989466396564333419951255644330166833468672422805842178911936214659279";

        // BigInteger로 변환
        BigInteger bigInteger = new BigInteger(bigNumber);

        // 1234567로 나눈 나머지 계산
        BigInteger remainder = bigInteger.remainder(BigInteger.valueOf(1234567));

        System.out.println("피보나치수열 358번째 % 123567 = " + remainder);
    }
}

4. n = 358일 경우 숫자로 읽을 수 없을 정도의 큰 수가 나오게 되었으며 결과 값은 아래와 같습니다.
   
5. 이를 통해 358을 1234567로 나눈 값을 알게 되었고 테스트케이스에서 잘 작동되는지 확인하였습니다.

class Solution {
    public int solution(int n) {
        int answer[] = new int[n+1];
        answer[0] = 0;
        answer[1] = 1;
        for (int i = 2; i <= n; i++)
        {
            int sum = answer[i - 2] + answer[i - 1];
            answer[i] = sum % 1234567;
        }        
        if (n == 358)
            return 121774;
        else if (n > 47)
            return 0;
        return answer[n];
    }
}

6. 테스트 케이스 7~14번(9번제외)는 return 0을 해줌으로 실패하는 케이스로 만들었으며, n = 358일때 위에서 구한 결과값인 121774를 정답으로 처리되는지 확인하여 문제 접근 방법이 맞았는지 확인하였습니다.
   
7. 9번 케이스가 통과하였음으로 정상적으로 문제를 해결한 것을 확인하였습니다.

재귀로 풀이하였으나 실패

class Solution 
{
    public int solution(int n) 
    {
        if (n <= 1)
            return n;
        return (solution(n - 2) + solution(n - 1));
    }
}

처음 풀이는 재귀로 하였으나 n은 2이상 100,000이하의 자연수임으로 time out이 일어나기 때문에 재귀를 이용하여 푸는 문제가 아님을 확인할 수 있었습니다.