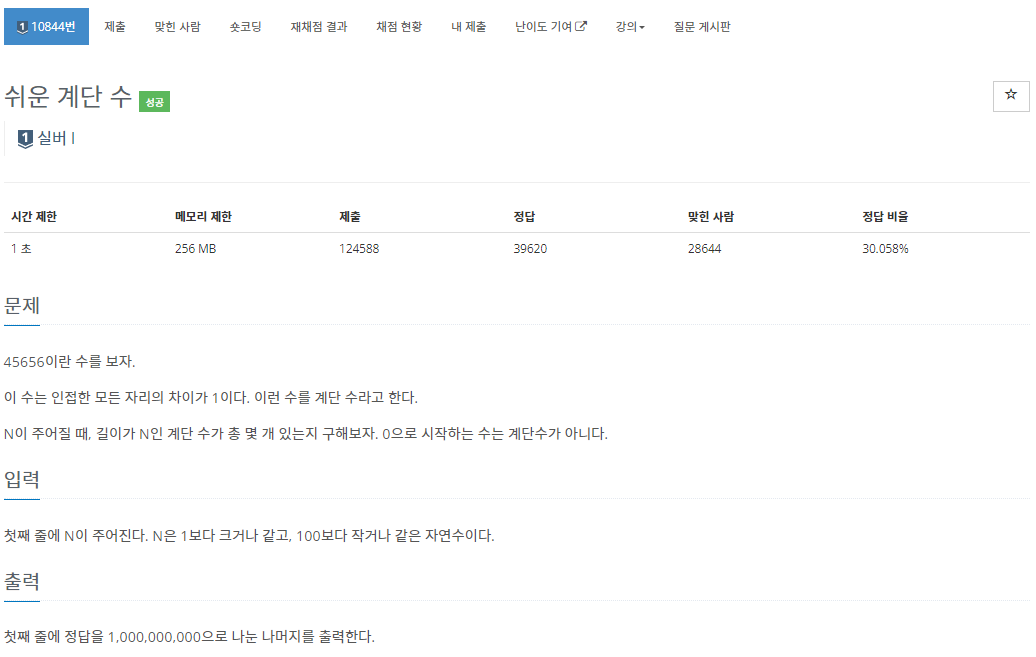
💡 문제
💬 입출력 예시
📌 풀이(소스코드)
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
public class Main {
private static final long MOD = 1000000000;
static int N;
static long[][] dp;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
N = Integer.parseInt(br.readLine());
dp = new long[N+1][10];
for (int i = 1; i < 10; i++) {
dp[1][i] = 1;
}
for (int i = 2; i <= N; i++) {
for (int j = 0; j < 10; j++) {
if (j == 0) {
dp[i][0] = dp[i-1][1] % MOD;
}
else if (j == 9) {
dp[i][9] = dp[i-1][8] % MOD;
}
else {
dp[i][j] = (dp[i-1][j-1] + dp[i-1][j+1]) % MOD;
}
}
}
long result = 0;
for(int i = 0; i < 10; i++) {
result += dp[N][i];
}
System.out.println(result % MOD);
}
}
📄 해설
- N번째 자릿수 : 길이가 N인 자연수에서 가장 왼쪽에 있는 수가 N번째 수
- 자릿값은 0~9 를 가질 수 있고, N개의 자릿값을 표현해야함 -> dp 테이블을 2차원 배열로 해야함
- 인접한 모든 자릿수가 1씩 차이가 난다 ->
dp[i][j] = dp[i-1][j-1] + dp[i-1][j+1]
- 유의할 점
- N번째 자릿수의 자릿값이 0 : 다음 자릿수의 자릿값은 1만 올 수 있음 ->
dp[i][0] = dp[i-1][1]
- N번째 자릿수의 자릿값이 9 : 다음 자릿수의 자릿값은 8만 올 수 있음 ->
dp[i][9] = dp[i-1][8]
후기


