알고리즘&자료구조 1편 - Big O Notation, 배열과 오브젝트의 성능

김영현·2023년 5월 15일

알고리즘 & 자료구조

목록 보기

1/6

코딩테스트를 준비하는건 문제를 풀면 된다.
문제를 풀기위한 지식을 습득하는건 강의를 들으면 된다.

드가자~

좋은코드란 무엇인가?

빠른것?
메모리를 적게 쓰는것?
읽기 쉬운것?
=> 세가지를 잘 조율해야한다.

우리는 일단 속도에 중점을 둬 보자.

1. 빠른것 = 시간 복잡도

//Add1.js
function addUpTo(n) {
  let total = 0;
  for (let i = 1; i <= n; i++) {
    total += i;
  }
  return total;
}

const t1 = performance.now();
addUpTo(1000000000);
const t2 = performance.now();
console.log(`시간 경과 : ${(t2 - t1) / 1000}초`);
//...시간 경과 : 0.9190668249949813초

//Add2.js
function addUpTo(n) {
  return (n * (n + 1)) / 2;
}

const t1 = performance.now();
addUpTo(1000000000);
const t2 = performance.now();
console.log(`시간 경과 : ${(t2 - t1) / 1000}초`);
//...시간 경과 : 0.00002681799978017807초

Add1과 Add2의 결과는 같다. 1부터 n까지의 합을 구하는 것. 하지만 속도차이는 어마무시하다. 이렇게 수동으로 속도를 비교할수도있지만, 같이 논의하기 어렵고 불확실하다.
1. 다른 기기끼리 시간측정 방식이 다름.
2. 같은 기계라도 시간의 오차가생김.
3. 빠른 알고리즘에선 아주 짧은시간안에 처리됨. 차이를 확인하기 어려움.

시간 대신 연산 갯수

Add2는 곱하기 덧셈 나누기
=> 총 세번의 연산을 한다. N의 값과 관계없이.
Add1은 N을 N번 더하고...total에 i를 더하고..어쩌고..5n+2번?
=> 정확한 숫자는 상관없다. 우리는 전체적인 추세를 볼것임. n이 커질수록 연산속도가 커진다

Introducing Big O

결국 Big O 표기법이란, 입력크기와 실행시간의 관계를 나타내는것. 자잘한 디테일(상수,계수)는 무시된다.
=> 수학의 극한과 비슷한것같다. 수많은 점을 찍고 그래프를 이어버리면 계수와 상수는 무시되기에.
Add1은 O(n), Add2는 O(1) 이렇게 표현할수 있음.

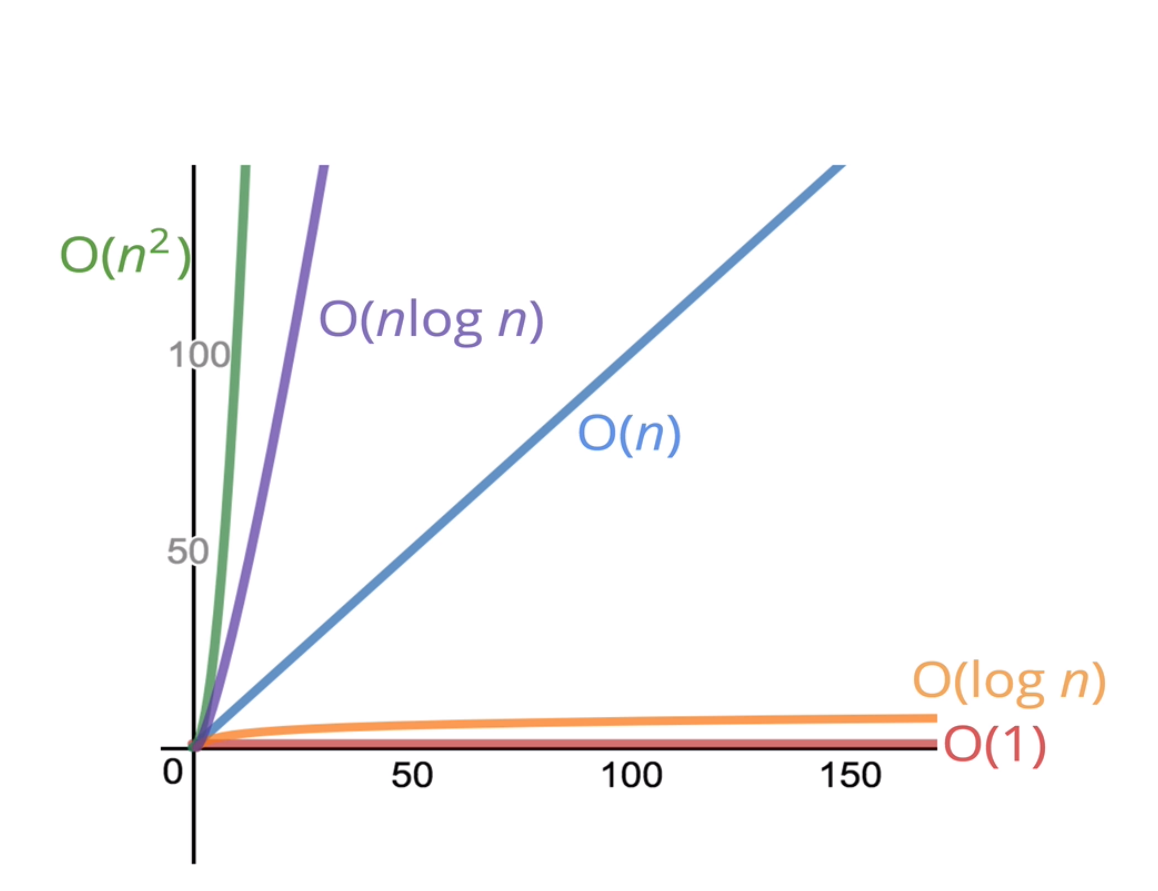
꿀팁

사칙연산이나 변수배정은 상수다.( O(1) )
index를 이용해 배열에 접근하는것도 상수다. || 객체의 데이터에 키로 접근하는것도 상수다.
루프가 있다면 복잡도는 루프의 길이*루프 내부 연산 이 된다.

2. 메모리를 적게 쓰는것 = 공간 복잡도

정확히 말하면 보조 공간의 복잡도를 구하는 것임
=> 공간 자체는 N이 무한대로 커지면 공간도 무한하게 필요하기때문에 의미가 없다. 알고리즘 자체에 의의가 있음. 입력공간은 무시한다!

Js에서의 공간복잡도

boolean, numbers, undefined, null은 모두 불변공간이다.
=> 입력의 크기와 상관없이 같은 크기를 지님
String은 O(n)의 공간이 필요하다.
=> 길이가 50인 문자열은 길이가 1인 문자열보다 공간을 50배 차지함.
reference type, array, object도 대부분 O(n)의 공간을 차지함.

function sum(arr){
  let total = 0;
  for(let i = 0; i < arr.length; i++){
    total += arr[i];
  }
  return total;
}

sum의 공간복잡도는 O(1).
=> 입력의 크기와 관계없이 let total = 0 과 let i = 0

function double(arr){
let newArr = [];
  for(let i = 0; i < arr.length; i++){
  newArr.push(2*arr[i]);
  }
  return newArr;
}

double의 공간복잡도는 O(n).
=> 내부에서 배열을 생성해서 리턴함.

Recap

알고리즘의 성능 분석을 하기위해서 Big O Notation을 사용함.
=> 입력 크가 늘어날수록 전체적 추세가변함.
Big O를 통해 시간과 공간복잡도에 대한 이해를 높임.
정확도가 아니라 전체적인 추세를 봄.
시간과 공간복잡도는 하드웨어의 영향을 받지않는 기준으로 함.
이제 알고리즘끼리 비교를 할수있다!

Array와 Object의 성능

Object는 언제 사용하는가?

정렬이 필요하지 않을때(인덱스로 구분할수 없음)
key를 기준으로 빠른 접근, 제거가 필요할때
=> 탐색O(n)을 제외한 입력, 제거, 접근의 시간복잡도는 O(1)임.
==> entries, keys, values는 탐색이기에 O(n). hasOwnProperty는 key값으로 찾는것이기에 O(1)

Array는 언제 사용하는가?

정렬이 필요할때
=> 주의!) 링크드 리스트나 더블 링크드리스크같은 자료구조도 정렬이 되며 배열보다 더 빠를때가 있음
인덱스를 기준으로 빠른 접근이 필요할때(입력, 제거는 위치에 따라 달라짐)
=> 맨 뒤에 추가, 제거하면 O(1), 맨 앞에 추가,제거 하면 엘리먼트의 인덱스를 추가한 엘리먼트의 갯수만큼 더하거나 빼줘야하기 때문에 O(n). 속도가 중요하다면 배열 앞에 추가/제거 하는것은 최대한 지양하자
==>push, pop은 끝에서 일어나기에 O(1). shift, unshift, concat, slice, splice, foreach/map/filter/reduce...etc는 O(n). sort가 특이하게 O(n*log n).
외울필요는 없다.

key나 index를 기준으로 접근하면 상수시간이라는 공통점이 있구나!