코딩테스트 준비 7편. 브루트 포스
브루트 포스.
brute : 난폭한, force : 힘.
난폭하게 힘으로 찍어누르는 알고리즘?
=> 그냥 할수있는건 다 해보는 알고리즘. == 완전탐색
ex) 무작위대입.
알고리즘별로 문제를 푸니, 역경에 부딪혔다. 브루트 포스 문제가 너무 어렵게 느껴진다.
한두문제 풀어보는데, 이게 맞나? 싶은 수준의 정답이 문제의 풀이다. 물론 난이도가 상승할수록 어느정도 최적화가 필요하지만.
브루트 포스가 굉장히 직관적으로 알고리즘을 짜야하기에 직감이 좋아야할듯 싶다. 물론 감각은 경험으로 커버가 가능하니, 많은 문제를 풀어야겠음.
일단 정리 드간다잉
gcd, lcm
greate common divisor.(최대공약수)
least common multiple.(최소공배수)
왠gcd하고 lcm이냐. 완전탐색으로 풀 수도 있는 문제라서 그렇다. 하지만 나는 그렇게 푸는걸 좋아하진 않는다.
아무튼.
초등학교때 배웠던 친숙한 아이들이지만, 시간이 지나며 까먹었다. 정수론에 나온다곤하나 나는 정수론을 배우지 않은 비전공자!
예전에 관련 문제를 풀어서 기억이 조금 있지만, 다시금 약수와 배수의 문제가 나와 복습해봤다.
30과 35의 최대 공약수를 구해보자.
가뿐하게 인수분해가 생각나겠지만, 소수 구해서 돌릴 시간에 다른방법을 찾는게 빠르다. 바로바로
유클리드 호제법
고대 + 그리스 + 수학자 삼위일체이신 유클리드선생님께서 만드신 알고리즘. 역시 고.그.수.
아무튼 무슨 법이냐면, a % b의 나머지가 r이라고 했을때, a,b 의 최대공약수는 b,r의 최대공약수와 같다는 것이다.
식으로 보는게 더 간단하다
- 35와 30의 나머지는 5.
- 30과 5는 바로 나눠지네? 그렇다면 b를 return.
곧바로 안나눠지는 예를 살펴보자.
- 44와 30의 나머지는 14.
- 30과 14는 바로 안나눠진다. 나머지 2가 발생. 발생했으니 다시 b와 r을 사용한다. 14와 2!
- 14와 2는...나눠진다. 그렇다면 b를 리턴!
요렇게 나타낼 수 있다. 재귀적으로 표현도 간단하다.
const gcd = (a,b) => {
if(a%b === 0) return b
return gcd(b,a%b);
}음!
유클리드 선생님은 바로 최소공배수까지 구해주신다. 최대공약수만 알면, 최소공배수는 식은죽껌밥먹기.
35와 30을 예로 들어보자. 최대 공약수는 5. 먼저 이해하기 쉽게 소인수분해를 해보자.
35 : 5x7
30 : 2x3x5
최소공배수는 서로에게 없는 약수를 곱해주는 것이다.
=> 2x3x5x7
하지만 두 자연수를 곱하게 되면, 최대공약수가 한번 더 곱해지게 된다
=> 2x3x5^2x7
그래서 두 자연수를 곱하고, 그 값을 최대공약수로 나누면, 최소공배수가 나오게 된다!
const lcm = (a,b) =>{
return (a*b)/gcd(a,b);
}요로꼬롬 최대공약수를 활용하면 된다. 결국 최소공배수를 구하려면 최대공약수를 구하면 된단얘기. 물론 완전탐색으로 하나한 찾아도 되지만, 이게 제일 빠르닷.
2차원배열
브루트포스에 생각보다 2차원배열을 전부 훑는문제가 많이 보였다...
=> 2차원 배열 + 브루트포스 조합에 아주 약한것을 알 수 있었다.ㅠㅠ
가령 이런 문제들이 나왔을때, 풀이를 안보면 풀수 없었다. 물론 실버5까진 얼추 할만한데...
7568번 덩치
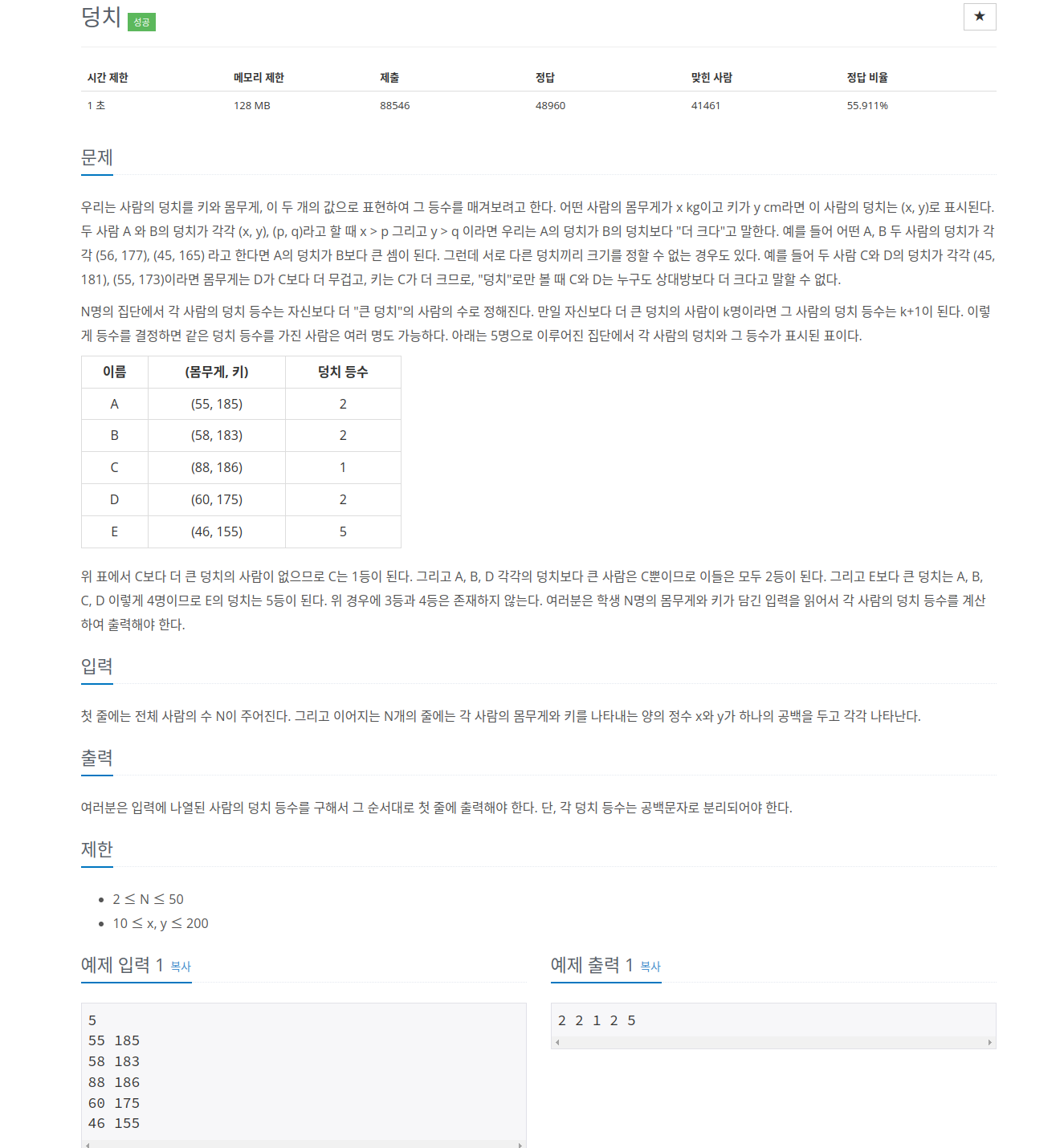
2차원 배열 자체를 훑는건 쉬웠다. 제일 큰 놈을 하나씩 골라내는 접근법으로 했었는데, 잘 안됐다. 한시간이 될때쯤 결국 풀이를 봤다.
풀이는 이랬다. 지정한 사람을 제외한 모든 사람과 x,y값을 동시에 비교(&&)해 자신보다 더 큰사람이 있으면 count를 ++해줬다. 나도 중첩 for문을 사용했는데, 안쪽 for문의 j값을 i+1로 뒀던게 문제였다. 생각해보니 자신을 제외한 모든사람하고 비교를 해야하니, j = 0으로 두곤, if(i !== j)일때만 값을 비교하면 되는거였다.
1018번 체스판 다시칠하기
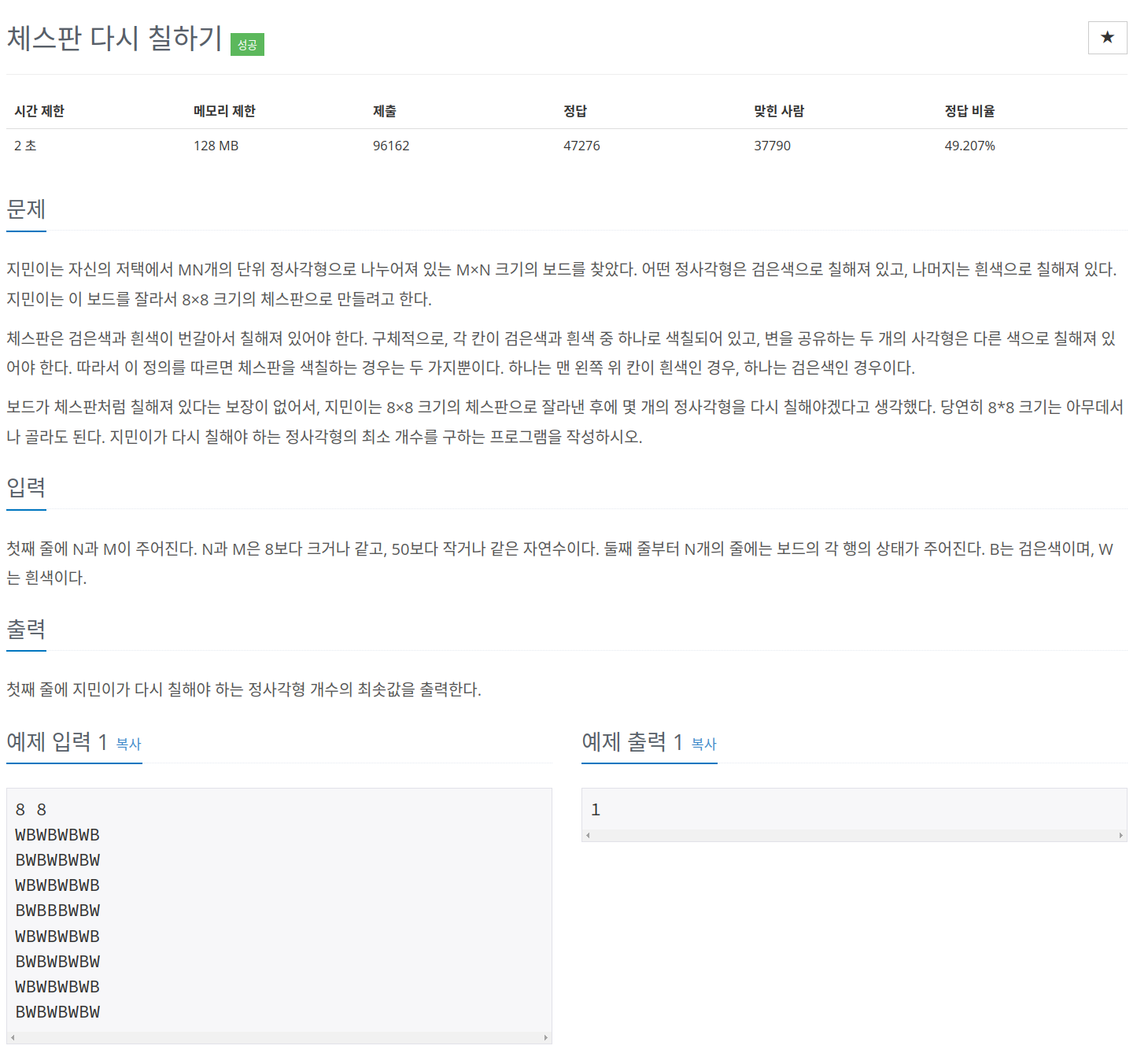
아. 이녀석이 다시금 좌절감을 안겨주었다. 아무리 해도 풀이가 생각나질 않았다. 갯수를 다 세는건 너무 노가다 같았다. 그래서 풀이를 봤는데, 8x8판을 체크하는게 인상적이었다. 주어지는 가로세로 길이는 8을 넘기때문에, 8x8판을 체크하려면 무려 4중첩 for문을 사용해야했다. 너무 당황스러웠다. 물론 x,y좌표로 2차원배열을 생각하는것도 헷갈렸지만, 일단 문제를 맞닥뜨렸을때 먼저 완전탐색으로 생각하는 버릇을 들여야겠다.
