전에 소개했던 삽입,선택,버블 정렬은 O(n)의 시간복잡도를 가졌다.
지금부터 소개할 정렬들은 O(N log n)의 시간복잡도를 가졌다!
가령 Merge Sort는 stable sort이면서 동시에 빠른 정렬 알고리즘이다!
잠깐, stable한 sort? 뭐가 안정적인걸까. 이것부터 짚고 넘어가자.
Stable Sort(안전한 정렬)
안전한 정렬이라니, 그렇다면 저번에 소개했던 정렬들은 안전하지 않다는건가?
여기서 쓰인 Stable은 중복된 값의 순서를 이전과 똑같이 보장한다는 소리다.
예제부터 보자
[ 5, 1, 1, 1, 3, 2 ] 라는 배열을 정렬해보자.
어떤 정렬을 하던 결과는 아래와 같을 것이다.
[ 1, 1, 1, 2, 3, 5 ]
하지만 우리는 중복된 값들의 순서를 정렬하기 전과 똑같이 유지하고싶다.
이럴때 필요한게 stable 한 sort이다.
=> 삽입, 버블, 병합은 stable한 sort이다.
Merge Sort(병합, 합병 정렬)
병합정렬은, 배열의 길이가 1 이하일때 정렬되었다 고 가정하는것이 핵심이다. 그렇게 정렬된 배열들을 서로 비교하며, 합쳐나가면 결국 정렬된 배열이 나온다.
- 초기 상태의 배열을 반씩 나눈다. 길이가 1이하일때까지!
- 그렇게 나뉜 배열들은 정렬되었다. 정렬된 두 배열을 비교하며 합쳐나간다
2-1. 정렬된 배열끼리 합칠땐, 맨 앞의 원소끼리만 비교하면 된다. - done!
이같은 메커니즘은 재귀적으로 이루어진다. 대부분의 분할-정복 알고리즘은 재귀를 이용하는것이 직관적임.
이해가 안간다면, 그림을 보자.
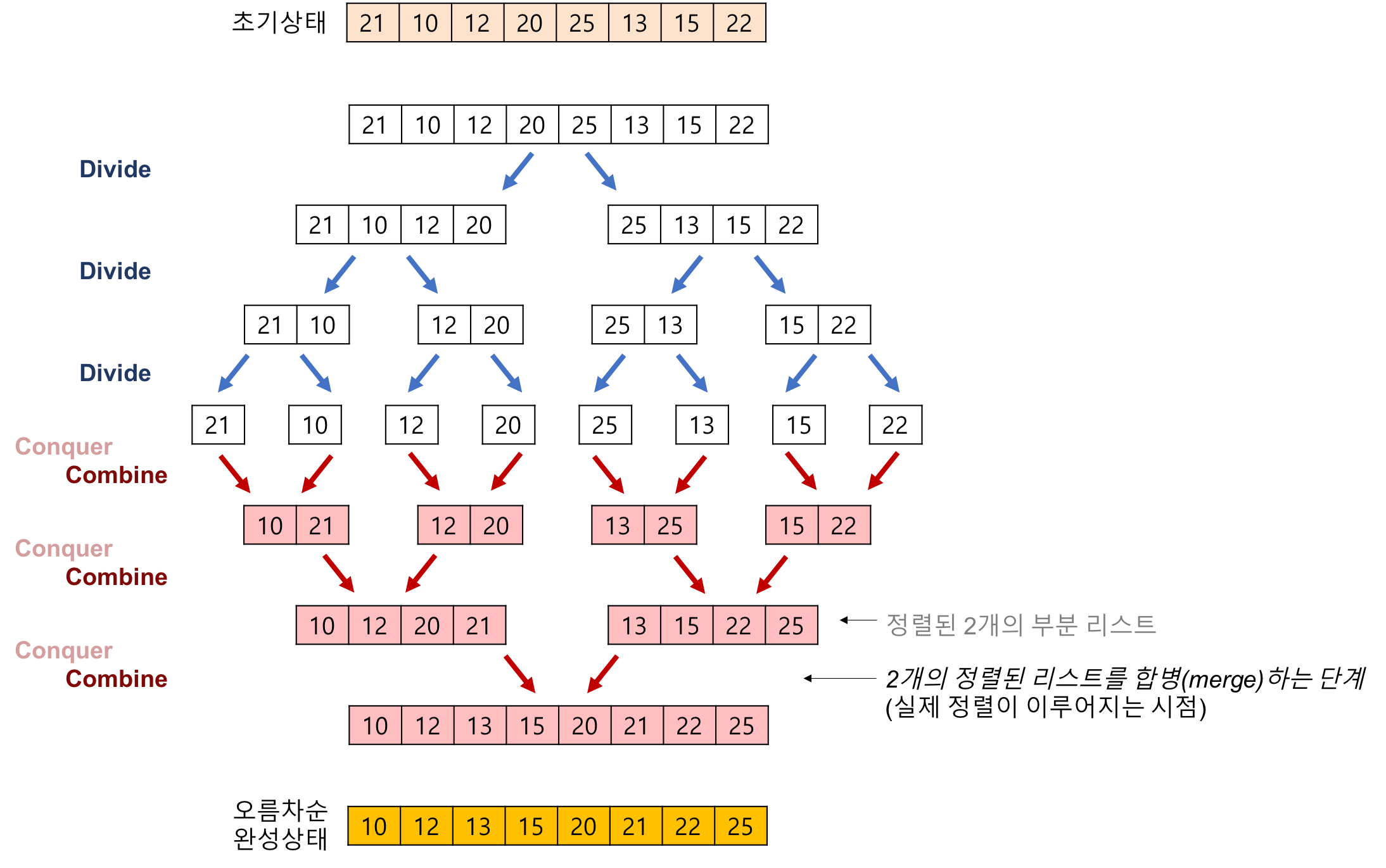
그림의 출처 : https://gmlwjd9405.github.io/2018/05/08/algorithm-merge-sort.html
코드로 나타내면 이렇다!
const merge = (arrLeft, arrRight) => {
let i = 0;
let j = 0;
const result = [];
while (i < arrLeft.length && j < arrRight.length) {
//두 배열 대소비교 후 작은거 부터 push 후 인덱스 증가
if (arrLeft[i] < arrRight[j]) {
result.push(arrLeft[i++]);
} else {
result.push(arrRight[j++]);
}
}
//남아있는 값들은 정렬된 값. result에 전부 푸쉬
while (i < arrLeft.length) {
result.push(arrLeft[i++]);
}
while (j < arrRight.length) {
result.push(arrRight[j++]);
}
return result;
};
//재귀적으로 반으로 나눈 후 합치기.
const mergeSort = (arr) => {
if (arr.length < 2) return arr;
const mid = Math.floor(arr.length - 1 / 2);
const left = mergeSort(arr.slice(0, mid));
const right = mergeSort(arr.slice(mid));
return merge(left, right);
};
console.log(mergeSort([9, 3, 1, 2, 7, 10, 5]));Quick Sort(퀵 소트)
이름 그대로 빠른 정렬! 대부분의 언어에서 지원하는 정렬 라이브러리는 이 퀵 소트를 사용해서 만든다.
하지만 큰 단점이 하나 존재한다.
바로 최악의 경우 시간복잡도가 O(n^2)이 된다는 것인데...왜 그런것인지는 퀵소트의 동작 원리를 알아야만 한다.
퀵소트의 메커니즘은 대략 이렇다
- pivot을 정한다. 중심축이 될 값이다. 아무거나 집지만, 통상적으로 첫번째 값을 잡음.
- pivot을 기준으로 작은값은 왼편, 큰 값은 오른편으로 보낸다.
2-1. 이중 포인터로 시작과 끝 인덱스를 잡고 i++, j-- 하면 됨. - pivot값 하나가 정렬된 위치로 왔다! 이걸 이제 피벗을 제외한 왼쪽, 오른쪽에 나눠서 재귀적으로 진행한다.
- 모든pivot이 정렬되었다. done!
참고로, 퀵소트는 inplace Sort이다.
대충감이 오지 않는가?
짤막하게 설명하자면, 추가적인 공간(배열)을 점유하지 않는 정렬이다.
왜 그런걸까 하면, 퀵 소트의 작동방식을 다시 생각해보면 된다.
pivot을 잡는것도, 왼쪽 오른쪽 나누는것도 불필요한 배열선언 없이 가능하다.
코드를 보면 이해가 더 빠르다.
const swap = (arr, left, right) => {
[arr[left], arr[right]] = [arr[right], arr[left]];
};
//start index와 endIndx 멀티플 포인터
const pivot = (arr, startIndex = 0, endIndex = arr.length - 1) => {
//타겟이 곧 피봇이
let target = arr[startIndex];
//자리를 바꿀 친구
let swapIndex = startIndex;
//피봇 + 1부터 시작해서, endIndex까지.
//왜 이하일까? endIndex에서 이미 -1을 했으니까!
for (let i = startIndex + 1; i <= endIndex; i++) {
//피봇이 더 크다면
if (target > arr[i]) {
//swapindex 값을 증가시키고,
swapIndex++;
//arr[swapIndex]와 arr[i]의 자리를 바꿈.
swap(arr, swapIndex, i);
}
}
//마지막에 바꾼 값 자리랑, 피봇 값을 바꾸면 피봇 왼편은 전부 피봇보다 작은 값들!.
//우측은 그럼 피봇보다 큰값들임.
swap(arr, startIndex, swapIndex);
return swapIndex;
};
function quickSort(arr, left = 0, right = arr.length - 1) {
if (left < right) {
const pivotIndex = pivot(arr, left, right);
//좌측 퀵정렬
quickSort(arr, left, pivotIndex - 1);
//우측 퀵정렬
quickSort(arr, pivotIndex + 1, right);
}
return arr;
}
console.log(quickSort([4, 6, 9, 1, 2, 5, 3]));이녀석은 다만 stable한 sort가 아니다. swap하는 과정에서 이전의 순서를 잃어버릴 가능성이 있기 때문이다. stable하게 만들순 잇지만, 퀵소트의 장점인 inplace sort를 해치게 된다!
Counting Sort(계수 정렬)
매우 간단한 정렬 방식이다.
우리는 [ 3, 5, 1, 1, 2 ]를 정렬하고싶다.
그래서 표를 만든다. 나는 배열로 만들어보겠다.
[ 0, 2, 1, 1, 0, 1 ] 감이 오는가? 바로 index 별로 등장한 값을 카운팅 한게 이 표다.
이 배열을 for문으로 돌면서 index의 값 만큼 push하기만 하면 원하는 결과를 얻을 수 있다.
const countingSort = (arr, numRange) => {
//일단 수의 범위를 알아야 한다!
const countArr = Array(numRange + 1);
const result = [];
for (let i = 0; i < arr.length; i++) {
if (!countArr[arr[i]]) {
countArr[arr[i]] = 1;
} else countArr[arr[i]] = countArr[arr[i]] + 1;
}
console.log(countArr);
for (let i = 0; i < countArr.length; i++) {
while (countArr[i]--) {
result.push(i);
}
}
return result;
};
console.log(countingSort([4, 1, 1, 1, 2, 3, 6, 4], 6));코드도 매우 간단쓰!
Radix Sort(기수 정렬)
계수가 아니라 기수 정렬이다. 처음봤을땐 꽤 난해했다.
우리는 이 배열을 기수정렬하고 싶다!
[23, 345, 5467, 12, 2345, 9852]
- 제일 큰 자리수를 구한다. 위 배열에선 4자리가 가장 큰 자릿수다.
- 1의자리, 10의자리 ....제일 큰 자릿수 순으로 숫자를 비교해서 배열에 넣는다.
2-1. 처음엔 1의 자리끼리 비교.[12, 9852, 23, 345, 2345, 5467]
2-2. 그 다음엔 10의 자리끼리[12, 23, 345, 2345, 9852, 5467]
2-3. 그다음엔 100의 자리끼리. 없는 자리면 0취급[12, 23 345, 2345, 5467, 9852]
이미 여기서 끝났지만, 1000의 자리도 비교해야함.
2-4. 1000의자리 비교. 위에서 바뀐건 없다[12, 23 345, 2345, 5467, 9852] - done!
코드로 나타내면 이렇다.
//1의자리, 10의자리, 100의자리...를 갖고오는 함수
const getDigit = (num, place) => {
return Math.floor(Math.abs(num) / Math.pow(10, place)) % 10;
};
const digitCount = (num) => {
//자릿수를 센다.
return Math.abs(num).toString().length;
};
//최고로 긴 자릿수 가져오기!
const mostDigits = (arr) => {
let result = 0;
for (let num of arr) {
result = Math.max(digitCount(num), result);
}
return result;
};
function radixSort(arr) {
const maxIteration = mostDigits(arr);
for (let i = 0; i < maxIteration; i++) {
const backet = Array.from({ length: 10 }, () => []);
for (let j = 0; j < arr.length; j++) {
const index = getDigit(arr[j], i);
backet[index].push(arr[j]);
}
arr = [].concat(...backet);
}
return arr;
}
console.log(radixSort([23, 345, 5467, 12, 2345, 9852]));이게 어떻게 가능하냐면, 초등학교때 배웠던 수의 비교를 생각하면 된다.
521과 630을 비교해본다. 제일 앞에있는 자릿수 부터 비교해서, 큰 자릿수가 이기는 거다.
6이 5보다 더 크니까, 630이 더 큰수다. 뭔가 이상하다. 기수정렬은 작은 자릿수부터 비교하는데...
답은 간단하다. 큰 자릿수부터 비교하면, 자릿수가 같은 녀석들은 제대로 정렬이 안된다.
[23, 345, 9997, 9996, 2345, 9152] 를 기준으로 설명해보겠다.
1. 1000의 자리 순으로 정렬한다. [23, 345, 2345, 9997, 9996, 9152,]
2. 100의 자리 순으로 정렬한다. [23, 9152, 345, 2345, 9997, 9996]
이미 여기서 부터 이상해진다!
참고로 counting sort와 radix sort는 서로의 값을 비교하면서 정렬하는 알고리즘이 아니다.
nonCompare 이었던가..
끝!
