학습내용

---

Linear Regression

Regression이란?

• 관찰된 연속형 변수들에 대해 두 변수 사이의 모형을 구한 뒤 적합도를 측정하는 분석 방법이다.

---

Linear Regression이란?

• 선형 회귀는 종속 변수($y$)와 하나 이상의 독립 변수($x$) 간의 관계를 모델링하는 통계적 방법이다.
• 일반적인 방정식은 다음과 같다.

  $y = mx + b$

• 여기서 $y$는 종속 변수, $x$는 독립 변수, $m$은 회귀 계수, $b$는 y절편(bias)이다.

---

Linear Regression의 가정

• Linear Regression은 4가지의 가정이 존재한다.
  • 선형성 : 종속 변수와 독립 변수 간의 관계가 선형적이어야 한다.
  • 독립성 : 관측값들은 서로 독립적이어야 한다. 실제값과 예측값의 차이(잔차)가 무작위로 분포되어 있어야 한다. 시간의 흐름에 따라 잔차가 특정 패턴을 보이면 독립성 가정에 위배된다.
  • 등분산성 : 오류의 분산이 일정해야 한다. 잔차들이 일정한 분포로 위치해야 한다. 특정 구간에서 잔차의 분산이 달라지면 등분산성 가정이 위배된다.
  • 정규성 : 오류가 정규 분포를 따른다. 잔차들이 정규 분포를 따를 경우, 점들이 대각선에 가깝게 위치한다.

---

모델 평가 지표

평균 절대 오차 (MAE)

• 예측 값이 실제 값과의 차이를 절대값으로 계산하여 평균을 낸 것이다.
• 모든 오차를 동일하게 고려하기 때문에 해석이 용이하고, 단위가 종속 변수 즉, 결과값과 동일하다.

  $MAE = \frac{1}{n}\sum^n_{i = 1}|y_i-\hat{y_i}|$

---

평균 제곱 오차 (MSE)

• 예측 값과 실제 값의 차이를 제곱한 것의 총합을 평균낸 것이다.
• 오차를 제곱하므로 큰 오차에 더 민감하게 반응하기 때문에 큰 오차에 대해서는 더 큰 패널티를 부여한다.
• 큰 오차에 더 큰 패널티를 부여하기 때문에 모델의 큰 오차를 줄이는데는 유용하게 사용된다.
• 하지만 제곱을 사용하기 때문에 종속 변수와 단위가 다를 수 있다.
• 모델의 큰 오차를 중요하게 다루어야 하는 경우에 주로 사용된다.

  $MSE = \frac{1}{n}\sum^n_{i = 1}(y_i - \hat{y_i})^2$

---

제곱근 평균 제곱 오차 (RMSE)

• MSE에 제곱을 취한 값이므로 이름에도 Root가 추가된 모습이다. MSE와 같은 장점을 가짐과 동시에 종속변수와 단위가 다를 수 있는 문제를 제곱근을 사용함으로 해결하였다.
• 해석이 MSE보다 쉬우며, 큰 오차에 민갑하게 반응하지만 종속변수와 같은 단위를 유지한다.
• 일반적으로 많이 사용되며, 단위의 해석이 중요한 경우에 특히 자주 사용된다.

  $RMSE = \sqrt{\frac{1}{n}\sum^n_{i = 1}(y_i - \hat{y_i})^2}$

---

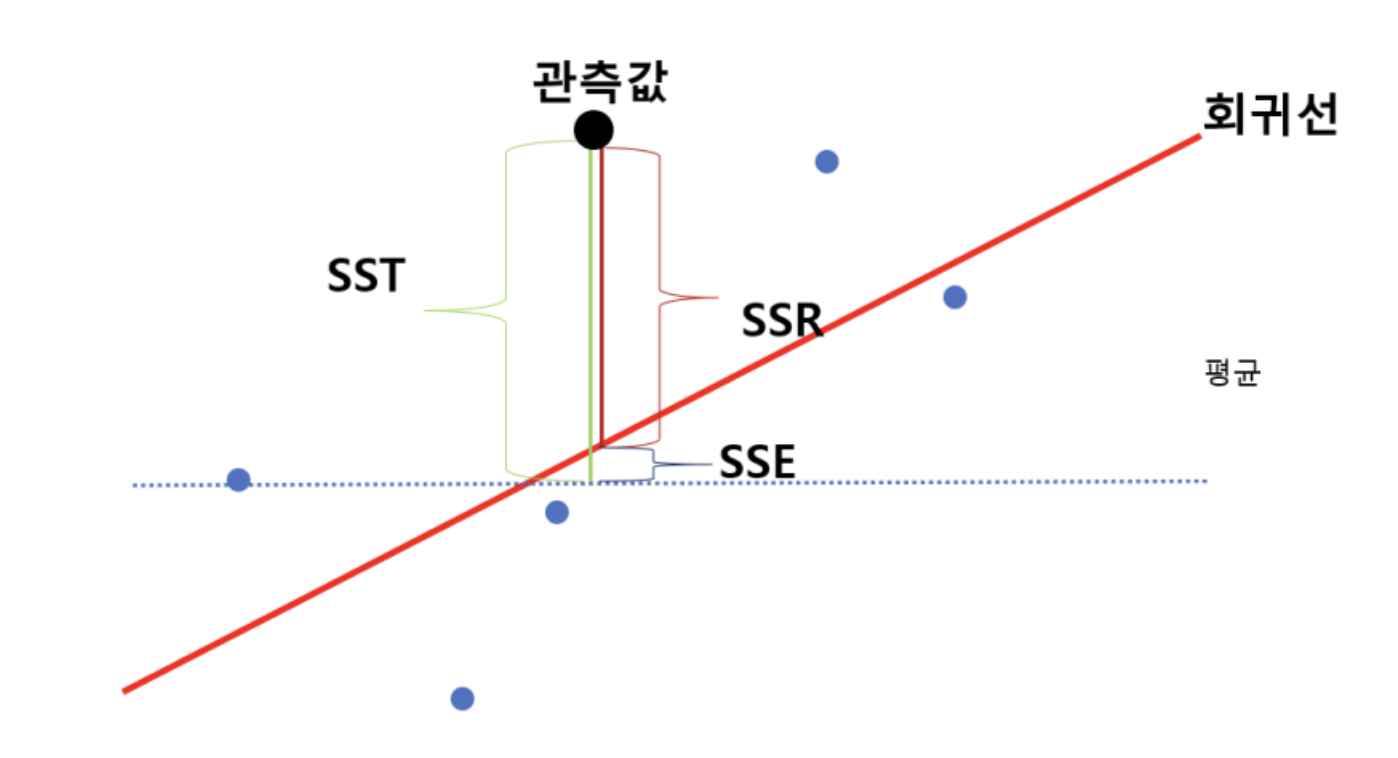
결정 계수 ($R^2$)

• 모델이 종속 변수의 변동성을 얼마나 설명하는지를 나타내는 지표이다.
• 값은 0 ~ 1사이의 범위를 가지며, 1에 가까울수록 모델이 데이터를 잘 설명하는 것을 의미한다.
• 비교적 해석이 쉽고 다른 모델과 비교하는 경우에 용이하다.
• 모델의 설명력을 설명해야할 때 사용되며, 특히 다른 모델과 비교를 하는데 유용하게 사용된다.
• SSE와 SST가 비슷할수록 예측값이 실제값을 잘 표현했다는 뜻이므로 1에 가까울수록 모델이 데이터를 잘 설명했다는 것을 의미한다.

  $R^2 = \frac{SSE}{SST} = 1 - \frac{SSR}{SST} \\ SST(Total\; Sum\; of\; Squares) = \sum^n_{i = 1}(y_i - \bar{y})^2 \\ SSE(Explained\; Sum\; of\;Squares)= \sum^n_{i = 1}(\hat{y_i} - \bar{y})^2 \\ SSR(Residual\; Sum\; of\; Squares) = \sum^n_{i = 1}(y_i - \hat{y_i})^2 \\$

  $$

---

NN Classifier

• 학습된 데이터 중에서 입력으로 들어온 데이터와 가장 유사한 것을 찾아 가장 유사한 데이터의 레이블로 예측하는 것이다.
• 그렇기에 train 단계에서는 모든 데이터와 라벨을 기억하면 되는 것이기 때문에 O(1) 시간 복잡도를 가지고, test 단계에서는 모든 학습 데이터를 확인하면 가장 유사한 데이터를 찾아야하기 때문에 O(n)의 시간 복잡도를 가진다.
• 입력 데이터의 라벨을 예측하기 위해서는 두 데이터 간의 유사도(또는 거리) 메트릭이 필요하다.

---

K-Nearest Neighbor Classifier

• NN Classifier은 가장 가까운 데이터의 라벨을 복사하여 예측하지만, KNN은 가장 가까운 k개의 데이터의 과반수 득표를 하는 방식으로 진행된다.

---

NN Classifier 계열의 문제점

• 이미지 분류에 있어서 이미지의 픽셀들은 거리에 대한 정보를 담고 있지 않다. 그렇기 때문에 데이터 간의 거리를 통해 예측을하는 NN Classifier은 이미지 분류에서 사용되지 않는다.
• 이미지 분류시 테스트할 경우 이미지에서 거리 정보를 담고있는 데이터를 따로 추출해 진행해야 하기때문에 매우 느린 속도를 가지고 있다.
• 차원의 저주 : 고차원의 데이터의 경우 기하급수적으로 증가하는 예제 수가 필요하다. 차원이 증가할 수록 데이터들간의 거리가 비슷해지는 경향이 있기 때문이다.
• 데이터 표현의 문제 : 이미지 데이터에서 픽셀 간 거리를 사용할 경우, 이미지의 구조적, 의미적 정보를 손실하는 문제가 있다.